[세상에서 가장 쉬운 통계학 입문] 을 읽고 -t분포

---

t분포

: 모평균 이외의 것은 '현실에서 관측된 표본'으로 계산할 수 있는 통계량

1.t분포

• 통계량 T 계산법
  1단계
  데이터 n개의 표본평균 $\bar{x}$ 를 계산한다.
  ($\bar{x}$ = $\frac{x_1+x_2+...+x_n}{n}$으로 계산한다. )

  2단계
  데이터 n개의 표본표준편차 s를 계산한다.
  (s=$\sqrt{\frac{(x_1-\bar{x})^2+(x_2-\bar{x})^2+...+(x_n-\bar{x})^2}{n}}$ 으로 계산한다. )

  3단계
  표본평균 $\bar{x}$ 에서 모평균 $\mu$를 빼고, 표본표준편차 s로 나누며,
  데이터수에서 1을 뺀 수에 루트를 한 $\sqrt{n-1}$를 곱한다.
  이것이 통계량 T가 된다.
  T=$\frac{(\bar{x}-\mu)\sqrt{n-1}}{s}$
  => 모평균 이외에는 모두 관측된 데이터만으로 계산
  =>따라서, T의 분포를 안다면 95% 예언적중구간을 만들 수 있고,
  모평균 $\mu$를 구간추정 할 수 있다.

2.t분포의 히스토그램

• 통계량 T=$\frac{(\bar{x}-\mu)\sqrt{n-1}}{s}$의 분포를 '자유도 n-1 인 t분포'라고 부른다.
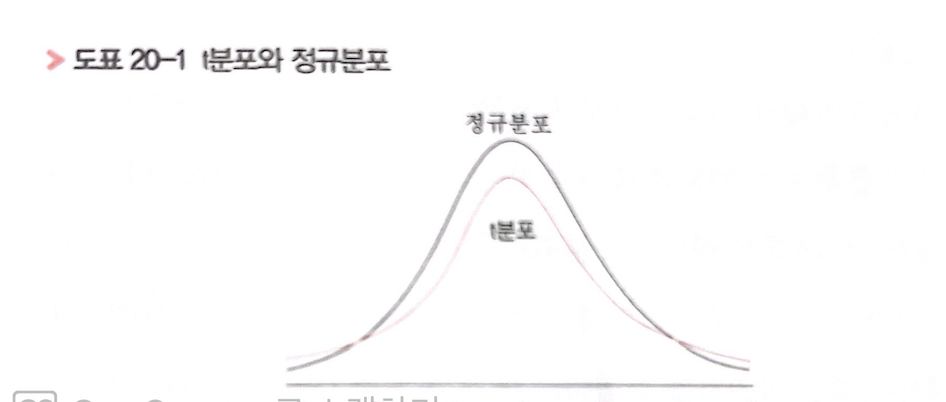
  =>이 분포는 정규분포와 아주 비슷하지만,정규분포보다 볼록한 부분이 약간 낮고, 그만큼 완만한 곳은 높다.

  

  => 자유도 (표본수 -1)가 커짐에 따라,
  점점 가운데가 볼록한 그래프가 된다
  (0에 가까운 상대도수가 커진다는 의미)

3.t분포의 정식적인 정의

• t분포의 정의
  t분포의 정식적인 정의
  T=$\frac{z\sqrt{k}}{\sqrt{W}}$
  =(표준정규분포의 데이터z) x $\sqrt{(W의 자유도 k)}$ $\div$ $\sqrt{(카이제곱분포W)}$
  => 통계량 T는 자유도 k의 t분포를 한다.

---