LIS 알고리즘

알고리즘 출처 - 찬휘님 블로그

LIS 알고리즘이란?

최장 증가 부분 수열 문제에서 쓰이는 알고리즘.

그럼 최장 증가 부분 수열 문제란 뭘까?

(2, 8, 3, 7, 1, 9) 가 있을 때, 증가하는 가장 긴 부분 수열은 무엇일까?

(2, 8, 3, 7, 1, 9) -> (2, 3, 7, 9) 라고 할 수 있다. 이러한 문제를 풀기 위해 쓰이는 알고리즘이 LIS 알고리즘이다.

LIS의 길이를 구하기

LIS문제는 길이를 구하냐, 원소를 구하냐에 따라서 난이도가 좀 달라진다. 먼저 길이만 신경쓸 때를 알아보자.

1. DP를 이용하자

for(int k = 0; k<n; k++){
        length[k] = 1; // 최소 숫자 한 개이니까 1로 초기화.
        for(int i = 0; i < k; i++){
            if(arr[i] < arr[k])
                length[k] = max(length[k], length[i] + 1);
        }
    }

아이디어는 다음과 같다.

1. 부분 수열도 최소한 숫자 1개는 들어가니까 length[k] = 1로 초기화 해준다.

2. i가 0부터 k-1까지 순회를 한다. arr[k] 가 arr[i]보다 크다면, 부분 수열에 arr[i] 다음으로 arr[k]가 올 수 있다는 것을 의미한다.
   예를 들어, (2, 3, 5) 이 있다. k = 2이고 , i 는 0,1 이 들어갈 수 있다.
   
   - i 가 1일 때
   length[2] = 1 로 초기화가 되고, max(1,length[0] + 1) 은 2이다. 그래서 length[2] = 2가 들어간다. 실제로도 부분 수열은 (2,5)이니까.
   
   - i가 2일 때
   현재 length[2] = 2이고 , arr[2] > arr[1]이다. 현재 arr[1]까지 부분 수열은 (2,3) 이고, length[1] = 2이다. 근데 arr[2] > arr[1]이니까 부분 수열 끝에 arr[2]값이 들어올 수 있다는 뜻.
   고로 (2,3,5)가 되고, max(2, length[1]+1) = 3. length[2] = 3이 된다. length[i] + 1 의 의미는 바로 이런 것이다.

근데 이 알고리즘의 시간복잡도는 O(n^2)이라, n의 크기가 10만이 넘어가면 실행 시간이 어마무시하게 커진다.

2. 이분 탐색을 이용한다.

아이디어는 다음과 같다.

코드로 나타내면

#include <iostream>

using namespace std;
int arr[1001];
int lis[1001];
int binary_search(int start, int end, int target) {
    while (start <= end) {
        int middle = (start + end) / 2;

        if (lis[middle] < target)
            end = middle-1;
        else if(lis[middle] == target)
            return middle;
        else
            start = middle + 1;
    }
}


int main(){
    lis[0] = arr[0];
    int n;
    cin >> n;
    int i = 0;
    int j = 1;

    while(j<n){
        if(lis[i] < arr[j]){   // lis 맨 뒷값보다 크면.
            lis[i+1] = arr[j];
            i+= 1;
        }
        else    // 작다면 위치 찾아줘서 값을 넣어줌.
        {
            int index = binary_search(0,i,arr[j]);
            lis[index] = arr[j];
        }
        j+=1;
    }

    cout << i+1;
    return 0;
}

이 코드에 arr배열 설정 등 몇가지 자세한게 빠져있긴 한데, 느낌만 사려고 급하게 짜본 코드라 그렇다!

그런데 문제는, LIS를 이루는 원소의 값은 실제 LIS 원소의 값과 무관하다. 라는 것이다.

고로 길이를 구할 때만 사용가능하고, 값을 구할 때는 사용이 불가능하다.
왜냐하면 그림에서 마지막 수가 0이라고 생각해보면, 0,3,5가 되는 것인데, (0,3,5)라는 부분 수열은 존재할 수 없다.

LIS 배열 값 구하기

배열 값 구하는 방식은 이러하다.

arr원소 값 마다 lis의 몇 번째 index에 들어가는지 저장하는 idxarr배열을 선언한다.

idx배열의 끝에서부터 lis의 길이 - 1, 즉 lis배열 가장 끝에 들어가는 값부터 비교하면서 내려오면 된다.

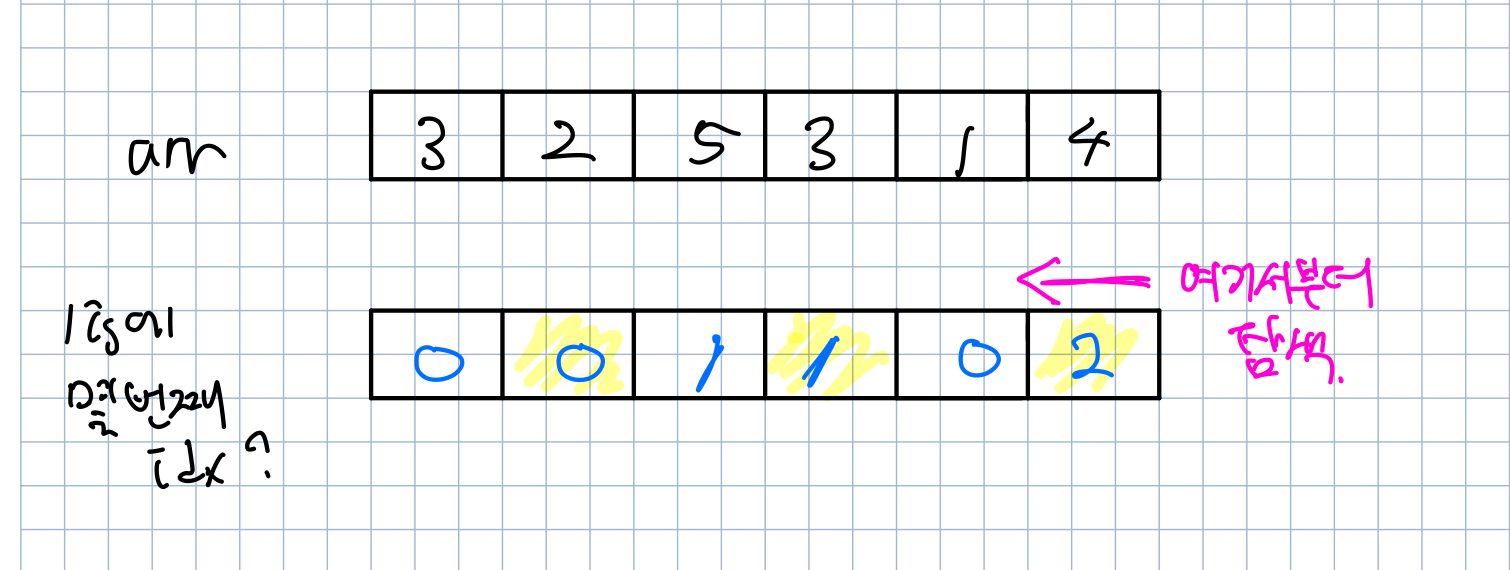
뒤에서 idx가 가장 큰 순서부터 탐색을 한다. 그리고 그 값들을 스택에 넣어주고 스택을 출력하면 역순으로 출력한다.

즉, (4,3,2) 값 순으로 들어가니까 스택에 넣고 출력하면서 (2,3,4) 순으로 나온다.

코드

#include <iostream>
#include <stack>

using namespace std;
int arr[1001];
int lis[1001];
int idxarr[1001];

int binary_search(int start, int end, int target){

    while(start < end){
        int middle = (start + end) / 2;

        if(lis[middle] > target)
            end = middle;
        else
            start = middle+1;
    }
    return end;
};

int main(){
    stack<int> s;
    int n;
    cin >> n;
    for(int a = 0; a<n; a++)
        cin >> arr[a];
    lis[0] = arr[0];
    idxarr[0] = 0;
    int i = 0;
    int j = 1;

    while(j<n){
        if(lis[i] < arr[j]){   // lis 맨 뒷값보다 크면.
            lis[i+1] = arr[j];
            idxarr[j] = i+1;
            i+= 1;

        }
        else    // 작다면 위치 찾아줘서 값을 넣어줌.
        {
            int idx = binary_search(0,i,arr[j]);
            lis[idx] = arr[j];
            idxarr[j] = idx;
        }
        j+=1;
    }

    cout << i+1 << endl;
    int idx = i;
    for (int k = n-1; k>=0; k--){
        if (idxarr[k] == idx) {
            s.push(arr[k]);
            idx--;
        }
    }
    while(s.size()!=0){
        cout << s.top() << " ";
        s.pop();
    }

    return 0;
}
`