확장 칼만 필터(레이더 추적)

선형 칼만 필터는 분명한 한계점이 존재한다. 이는 주변에 존재하는 거의 모든 시스템이 비선형성을 띄기 때문이다. 이를 해결한 것이 확장 칼만 필터(EKF)이며 EKF는 기본적으로 비선형 시스템을 선형화 시켜 얻은 선형 모델 $A, H$를 사용한다는 것이 가장 큰 개념이자 목적이다. EKF는 다음과 같은 비선형 시스템 모델을 고려한다.

$x_{k+1}=f(x_k)+w_k$ 1.1
$z_k=h(x_k)+v_k$ 1.2

여태까지 봐왔던 선형 칼만 필터와의 가장 큰 차이점은 행렬 $A$와 $H$가 $f()$와 $h()$의 형태로 변경되었다는 것이다. 즉 선형 행렬식이 비선형 함수로 나타내어 진다는 것이다. EKF의 알고리즘을 나타내는 식은 아래의 그림과 같다.

알고리즘

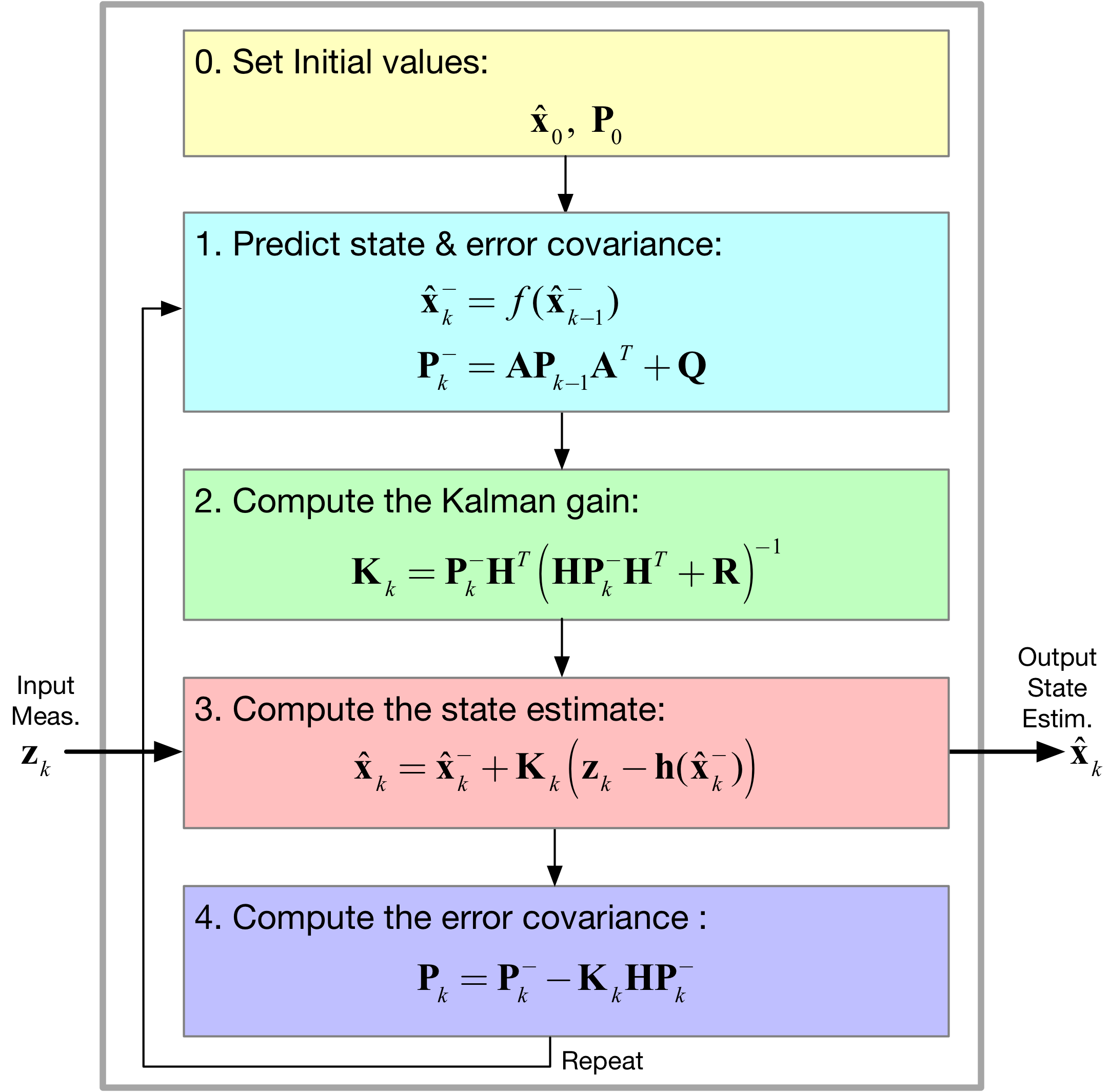
서론에서 언급하였듯이 EKF는 비선형 시스템을 선형화 시켜 얻은 선형 모델 $A, H$를 사용한다는 것이 가장 큰 개념이다. 비선형 시스템을 선형화 시키는 방법은 각 비선형 함수의 편미분(jacobian)을 구하는 것이다.

$A=\frac{\partial{f}}{\partial{x}}_{\hat{{x}}_k}$ 2.1
$H=\frac{\partial{h}}{\partial{x}}_{\hat{{x}}_k^-}$ 2.2

비선형 모델을 편미분해서 선형 행렬을 구하는 방법은 선형화의 대표적인 기법이다. 따라서 EKF는 미리 결정된 선형화 기준을 사용하지 않고, 직전 추정값인 $\hat{x}_k$를 기준으로 삼아 매번 새로운 선형 모델을 구하게 된다.

레이더 추적

이를 통한 첫번째 예제는 '레이더로 물체까지의 거리를 측정해서 이동 속도와 고도를 추정하기'이다. 이 예제에서 물체는 2차원 평면 상에서 일정한 고도와 속도를 유지하면서 움직인다고 가정한다.

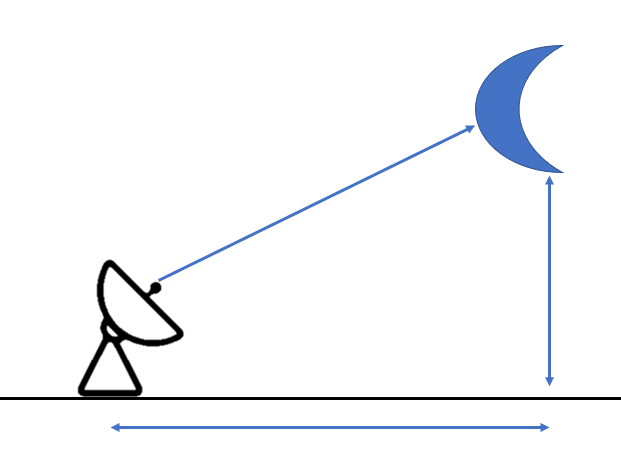
시스템 모델 설정

시스템의 상태 변수를 다음과 같이 설정한다.

$x=\begin{bmatrix}수평거리\\이동 속도\\고도\end{bmatrix}=\begin{bmatrix}x_1\\x_2\\x_3\end{bmatrix}$ 3.1

전제조건에서 물체의 이동 속도와 고도가 일정하다고 주어졌으므로 시스템 모델은 다음과 같이 표현된다.

$\begin{bmatrix}\dot{x_1}\\\dot{x_2}\\\dot{x_3}\end{bmatrix}=\begin{bmatrix}0&1&0\\0&0&0\\0&0&0\end{bmatrix} \begin{bmatrix}x_1\\x_2\\x_3\end{bmatrix}+\begin{bmatrix}0\\w_1\\w_2\end{bmatrix}$ 3.2

수평 거리의 변화율이 물체의 이동속도이므로 3.3임을 알 수 있다. 또한 이동 속도와 고도가 일정하므로 변화율이 0이다. 하지만 시스템 잡음을 고려하여 $w_1, w_2$를 추가한다.

$\dot{x_1}=x_2$ 3.3
$\dot{x_2}=w_1$ 3.4
$\dot{x_3}=w_2$ 3.5

또한, 레이더의 측정값($z_k$)은 측정 잡음($v$)를 고려하여 4.1과 같이 표현된다.

$z_k=r=\sqrt{x_1^2+x_3^2}+v=h(x)+v$ 4.1

정리

최종적으로 행렬 $A,H$는 다음과 같다.

$f(x)=Ax$ 이므로 $A=I+\begin{bmatrix}0&1&0\\0&0&0\\0&0&0\end{bmatrix}*dt$ 5.1

$H=\begin{bmatrix}\frac{\partial{h}}{\partial{x_1}}&\frac{\partial{h}}{\partial{x_2}}&\frac{\partial{h}}{\partial{x_3}}\end{bmatrix}=\begin{bmatrix}\frac{x_1}{\sqrt{x_1^2+x_3^2}}&0&\frac{x_3}{\sqrt{x_1^2+x_3^2}}\end{bmatrix}$ 5.2

function [pos, vel, alt] = RadarEKF(z, dt)

persistent A Q R
persistent x_hat P
persistent firstRun


if isempty(firstRun)
    A = eye(3) + dt * [0,1,0;
                       0,0,0;
                       0,0,0];
    Q = [0,0,0;
         0, 0.001, 0;
         0, 0, 0.001]; % w_k의 공분산 행렬

    R = 10; % v_k의 공분산 행렬

    x_hat = [0, 90, 1100]'; % 임의로 예측한 초기 추정값
    P = 10 * eye(3);

    firstRun = 1;
end

H = Hjacob(x_hat); % 시스템 행렬의 야코비안 H 계산
xp = A * x_hat;
Pp = A*P*A' + Q;

K = Pp*H'*inv(H*Pp*H' + R);

x_hat = xp + K*(z-hx(xp));
P = Pp - K*H*Pp;

pos = x_hat(1);
vel = x_hat(2);
alt = x_hat(3);

end

%------------------------

function zp = hx(xhat)

x1 = xhat(1);
x3 = xhat(3);

zp = sqrt(x1^2 + x3^2);

end

%------------------------

function H = Hjacob(xp)

H = zeros(1, 3);

x1 = xp(1);
x3 = xp(3);

H(1) = x1 / sqrt(x1^2 + x3^2);
H(2) = 0;
H(3) = x3 / sqrt(x1^2 + x3^2);

end

EKF를 사용할 때 가장 주의할 점은 최초로 실행할 때 선형 모델을 계산할 수 없다는 점이다. 그러므로 상태변수의 초기 추정값을 잘 설정해야 하며 초깃값의 오차가 크면 이 값으로 구한 선형 모델과 실제 시스템의 차이가 많이 나게 되어 결국 알고리즘이 발산할 위험이 존재한다는 것이다. 따라서 목표로 하는 시스템을 잘 분석하여 최대한 정확한 초깃값을 설정하여야 한다.

결과

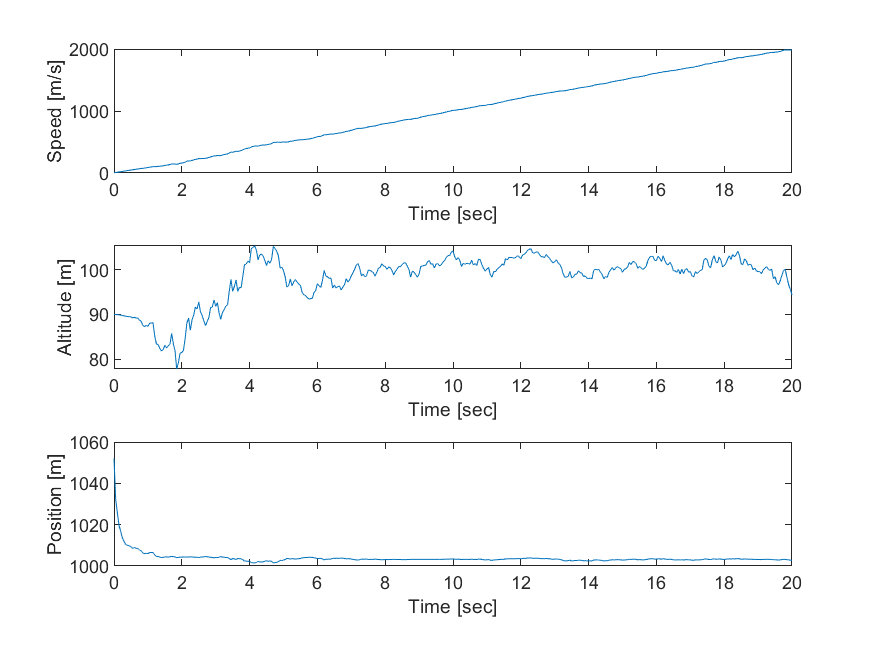
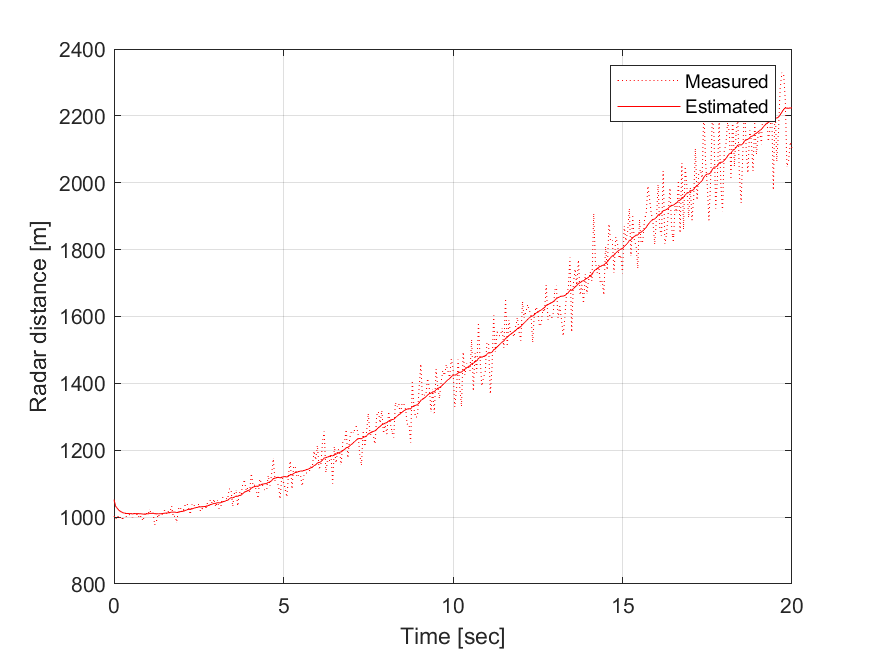
위의 그래프에서 첫번째를 확인해보면 실제 고도 데이터의 평균은 1000m인데 이를 잘 추정해내었고 또한 실제 이동속도인 100m/s를 기준으로 추정해낸 것을 볼 수 있다. 측정하지 않은값인 물체의 이동속도와 고도를 추정해내는 칼만 필터의 효과를 다시한번 확인할 수 있으며 레이더로 측정한 거리의 잡음도 효과적으로 제거한 것을 볼 수 있다.

참고

칼만 필터는 어렵지 않아 - 김성필 저, 한빛아카데미