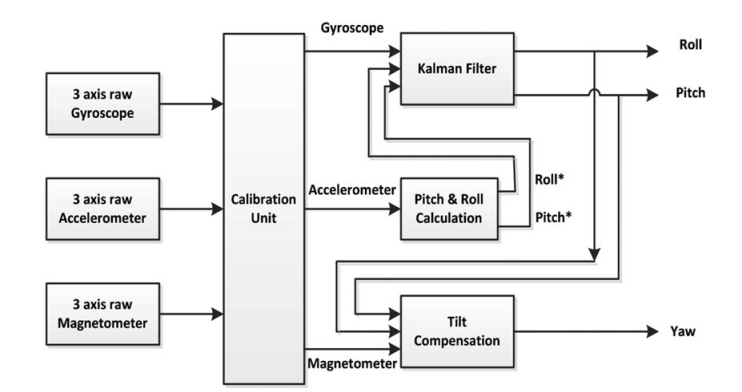
확장 칼만 필터(자이로,가속도 센서융합)

이 포스트는 EKF의 성능을 확인하기 위한 것으로 이전 포스트인 자이로센서, 가속도센서의 융합을 선형 칼만 필터에서 EKF로 대체하였다.

시스템 모델 설정

이전 포스트에서는 상태변수를 quaternion으로 두었던 것과 달리 EKF에서 시스템 모델의 상태 변수는 오일러 각도로 지정한다.

$x=\begin{bmatrix}\phi\\\theta\\\psi\end{bmatrix}$

각각 roll($\phi$), pitch($\theta$), yaw($\psi$)를 뜻한다. 이를 토대로 시스템 모델을 정의한다.

$\begin{bmatrix}\dot{\phi}\\\dot{\theta}\\\dot{\psi}\end{bmatrix}=\begin{bmatrix}1&\sin{\phi}\tan{\theta}&\cos{\phi}\tan{\theta}\\0&\cos{\phi}&-\sin{\phi}\\0&\sin{\phi}/\cos{\theta}&\cos{\phi}/cos{\theta}\end{bmatrix}\begin{bmatrix}p\\q\\r\end{bmatrix}+w$ 1.1
$=\begin{bmatrix}p+q\sin\phi\tan\theta+r\cos\phi\tan\theta\\q\cos\phi-r\sin\phi\\q\sin\phi\sec\theta+r\cos\phi\sec\theta\end{bmatrix}+w$ 1.2
$=\begin{bmatrix}f_1\\f_2\\f_3\end{bmatrix}+w$ 1.3
$=f(x)+w$ 1.4

1.1~1.4는 동일한 수식을 나타낸다. 삼각함수끼리 서로 곱해져 있는 형태로 상당히 심한 비선형 시스템이다. 다음으로 측정 모델식을 정의한다. 가속도 센서로는 yaw를 구할 수 없으므로 측정 모델은 다음과 같다.

$z=\begin{bmatrix}1&0&0\\0&1&0\end{bmatrix}\begin{bmatrix}\phi\\\theta\\\psi\end{bmatrix}+v$ 2.1
$=Hx+v$ 2.2

행렬 $A$를 구하기 위해선 $f(x)$의 jacobian을 구해야 하며 이는 아래와 같이 정의된다.

$A=\begin{bmatrix}\frac{\partial f_1}{\partial \phi}&\frac{\partial f_1}{\partial \theta}&\frac{\partial f_1}{\partial \psi}\\\frac{\partial f_2}{\partial \phi}&\frac{\partial f_2}{\partial \theta}&\frac{\partial f_2}{\partial \psi}\\\frac{\partial f_3}{\partial \phi}&\frac{\partial f_3}{\partial \theta}&\frac{\partial f_3}{\partial \psi}\end{bmatrix}$ 3.1

알고리즘

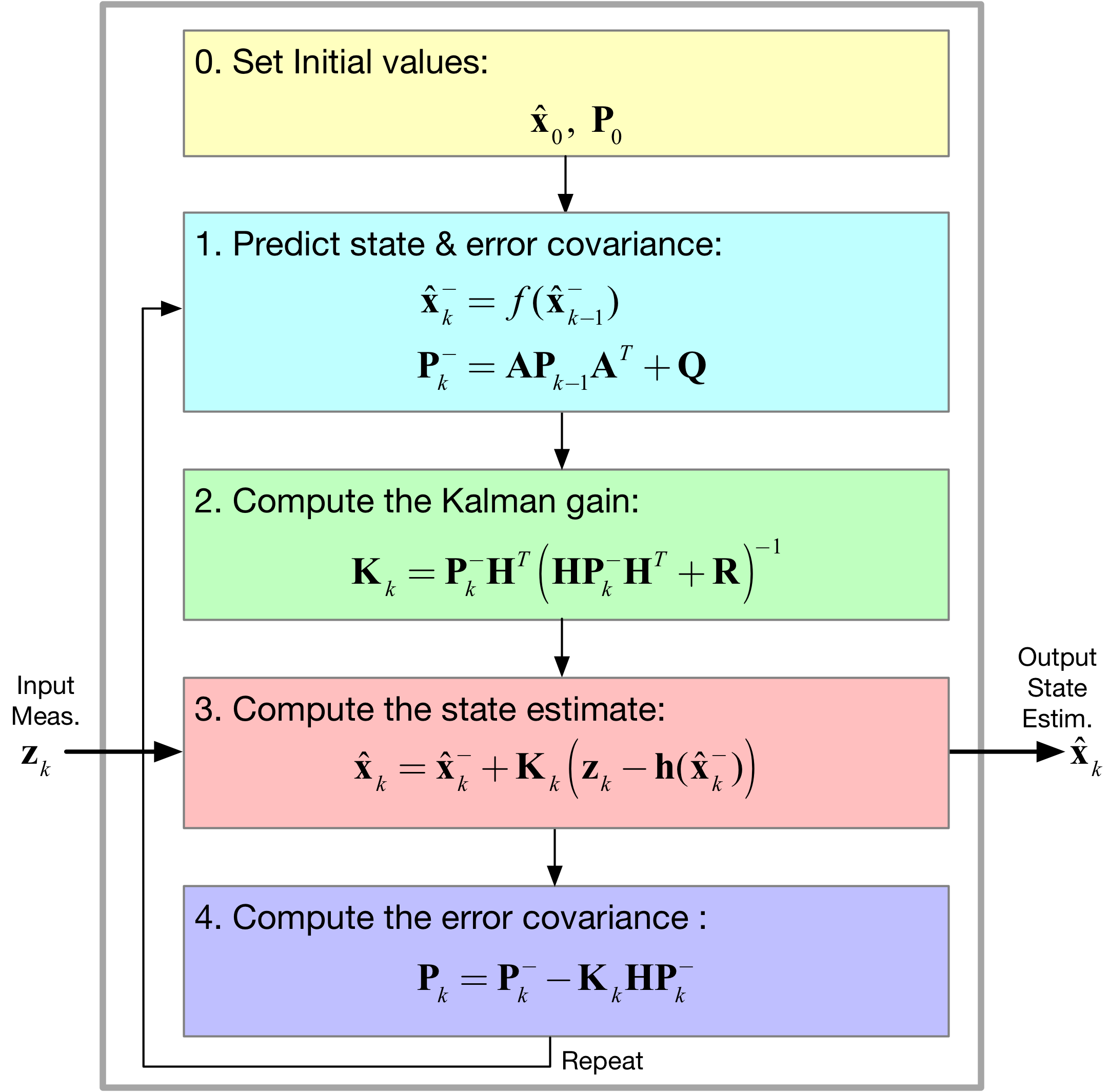
정리

최종적으로 EKF에 대한 코드는 아래와 같다.

function [phi, theta, psi] = EulerEKF(z, rates, dt)

persistent H Q R
persistent x_hat P
persistent firstRun


if isempty(firstRun)
    % accelerometer can't measure yaw rate
    H = [1, 0, 0;
         0, 1, 0];
    
    % system noise
    Q = [0.0001, 0, 0;
         0, 0.0001, 0;
         0, 0, 0.1];
    
    % measurement noise
    R = [10, 0;
         0, 10];

    x_hat = [0, 0, 0]'; % initial state variable(roll=0, pitch=0, yaw=0)

    P = 10 * eye(3); % initial covariance

    firstRun = 1;
end

A = Ajacob(x_hat, rates, dt);

% step 1: Predict state & error covariance
xp = fx(x_hat, rates, dt);
Pp = A*P*A' + Q;

% step 2: Compute Kalman gain
K = Pp*H'*inv(H*Pp*H' + R);

% step 3: Compute the state estimate
x_hat = xp + K*(z - H*xp);

% step 4: Compute the error covariance
P = Pp - K*H*Pp;

phi = x_hat(1);
theta = x_hat(2);
psi = x_hat(3);

%------------------------
% function xp:
% Compute the angular velocity(p, q, r) to euler rate
% return predicted x
function xp = fx(xhat, rates, dt)

phi = xhat(1);
theta = xhat(2);

p = rates(1);
q = rates(2);
r = rates(3);

xdot = zeros(3, 1);
xdot(1) = p + q*sin(phi)*tan(theta) + r*cos(phi)*tan(theta);
xdot(2) = q*cos(phi) - r*sin(phi);
xdot(3) = q*sin(phi)*sec(theta) + r*cos(phi)*sec(theta);

xp = xhat + xdot*dt;

%------------------------
% function Ajacob:
% Compute the jacobian matrix of f(x)
% return A
function A = Ajacob(xhat, rates, dt)

A = zeros(3, 3);
phi = xhat(1);
theta = xhat(2);

p = rates(1);
q = rates(2);
r = rates(3);

A(1, 1) = q*cos(phi)*tan(theta) - r*sin(phi)*tan(theta);
A(1, 2) = q*sin(phi)*sec(theta)^2 + r*cos(phi)*sec(theta)^2;
A(1, 3) = 0;

A(2, 1) = -q*sin(phi) - r*cos(phi);
A(2, 2) = 0;
A(2, 3) = 0;

A(3, 1) = q*cos(phi)*sec(theta) - r*sin(phi)*sec(theta);
A(3, 2) = q*sin(phi)*sec(theta)*tan(theta) + r*cos(phi)*sec(theta)*tan(theta);
A(3, 3) = 0;

A = eye(3) + A*dt;

코드에 대해 잠깐 설명을 덧붙이자면 A = eye(3) + A*dt, xp = xhat + xdot*dt와 같이 작성되어 있다. 시스템 모델의 비선형 함수 $f(x)$가 오일러 각도의 변화율($\begin{bmatrix}\dot{\phi}\\\dot{\theta}\\\dot{\psi}\end{bmatrix}$)에 의해 정의되어 있으므로 A*dt가 타당할 것이다. 또한 단위행렬인 I가 더해져 있는 형태인데 자이로 센서는 상대적인 각속도를 측정하기 때문에 (0, 0, 0)라는 상태에서 절대적으로 얼마나 회전했는가를 파악하기 위해선 이전 값을 토대로 누적 합산하여 구할 수 있다. 따라서 최종적으로 A = eye(3) + A*dt와 같이 작성하였다. 또한, 예측값 xp의 경우 같은 이유로 비선형 함수 $f(x)$를 오일러 적분해야 하기 때문이다.

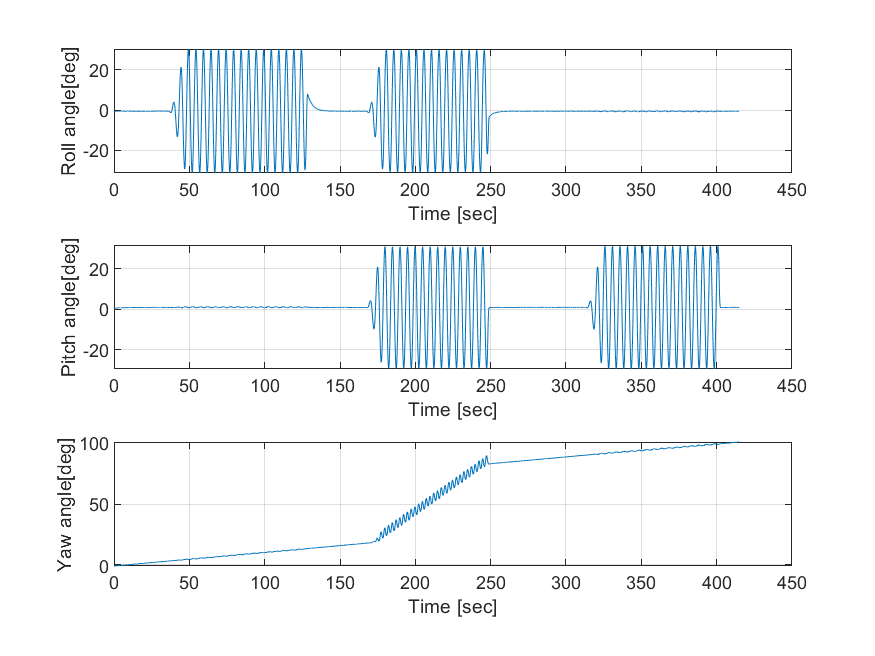
결과

참고

• Orientation estimation and movement recognition using low cost sensors
• Estimation of yaw angle from flight data using extended Kalman filter
• 칼만 필터는 어렵지 않아 - 김성필 저, 한빛아카데미