고주파 통과 필터

기본적으로 모든 신호, 데이터는 다음과 같은 방정식이 성립하게 된다.
측정값 = 참값 + 잡음

이를 통해 다음과 같은 방정식이 성립함을 알 수 있다.
참값 = 측정값 - 잡음

저주파 통과필터가 측정값-잡음의 참값을 출력했다면 반대로 고주파 통과필터는 잡음만을 추출해 내는 필터이다. 저주파 통과 필터나 고주파 통과 필터처럼 주파수의 관점에서 설계하는 필터는 대부분 라플라스 변환에 의해 그 특성을 파악하게 된다. 고주파 통과 필터의 전달 함수(transfer function)은 다음과 같다.

$G(s)=\frac{s}{s+a}$ 1.1
$\lim_{s \to 0}G(s)=\lim_{s\to0}\frac{s}{s+a}=0$ 1.2
$\lim_{s \to \infty}G(s)=\lim_{s\to\infty}\frac{s}{s+a}=1$ 1.3

$G(s)=\frac{Y(s)}{X(s)}$로 정의되므로 $s$가 0에 가까워지면 $G(s)$가 0이 되어 출력신호인 $Y(s)$를 차단시키고, $s$가 $\infty$에 가까워지면 $G(s)$가 1에 가까워져 입력신호 $X(s)$가 그대로 출력되는 것을 직관적으로 확인할 수 있다. 이를 코드로 작성하기 쉽게 만들기 위해 frequency domain에서 time domain으로 역변환 과정을 거치는 방법은 다음과 같다.

1) $G(s)=\frac{s/a}{s/a+a/a}$
분자와 분모 모두 $a$로 나눈다

2) $G(s)=\frac{\tau s}{\tau s + 1}$
$\tau=\frac{1}{a}$로 치환한다

3) $(\tau s + 1)Y(s)=(\tau s)X(s)$

4) $\tau\dot{y(t)}+y(t)=\tau\dot{x(t)}$
라플라스 역변환을 실행한다.

5) $\tau\frac{y_k-y_{k-1}}{\Delta t}+y_k=\tau\frac{x_k-x_{k-1}}{\Delta t}$
연속신호를 이산화한다.

6) $y_k=\frac{\tau}{\tau+\Delta t}y_{k-1}+\frac{\tau}{\tau+\Delta t}(x_k-x_{k-1})$
양변에 $\Delta t$를 곱하고 정리한다.

최종적으로 $\frac{\tau}{\tau+\Delta t}=\alpha$로 치환하면 다음과 같은 형태를 띄게 된다. LPF와 달리 현재의 입력값 외에 직전 입력값이 필요하다는 차이점이 존재한다.

$y_k=\alpha y_{k-1}+ \alpha(x_k-x_{k-1})$ Highpass Filter
$y_k=\alpha y_{k-1}+(1-\alpha)x_k$ Lowpass Filter

코드

function xhpf = HPF(u)

persistent prevX prevU
persistent dt tau
persistent firstRun

if isempty(firstRun)
    prevX = 0;
    prevU = 0;
    dt = 0.01;
    tau = 0.0233;

    firstRun = 1;
end

alpha = tau / (tau + dt);
xhpf = alpha*prevX + alpha*(u-prevU);

prevX = xhpf;
prevU = u;

결과

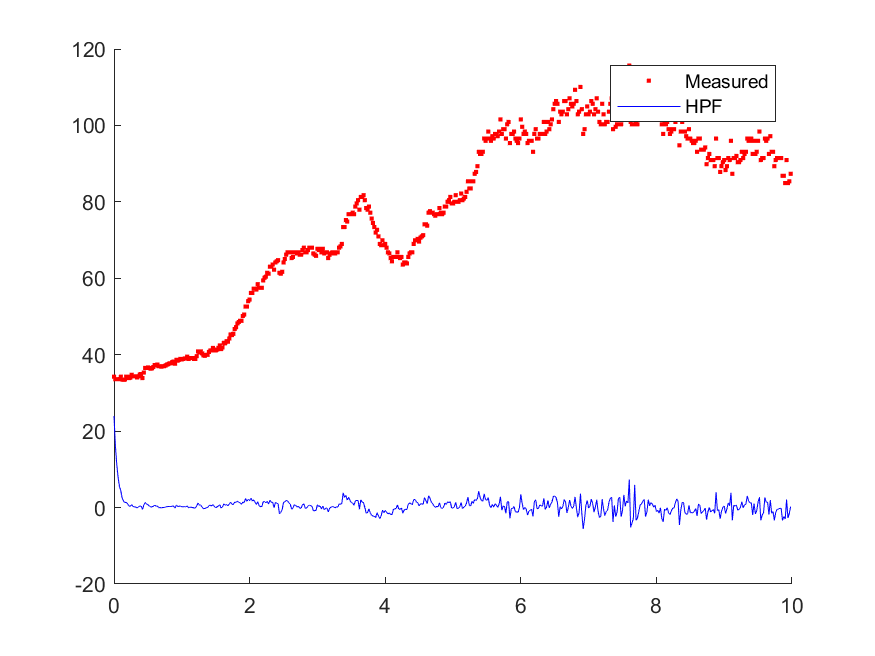
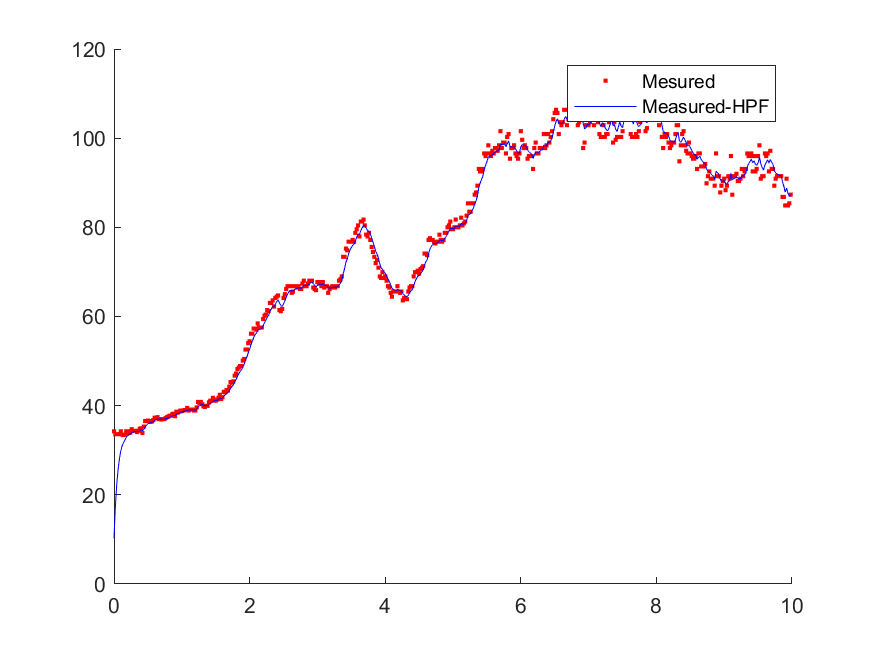
측정 신호값에서 HPF를 통과시켜 측정한 노이즈가 측정되었다. 위에서 정의한 참값 = 측정값 - 잡음에 의해서 측정값에 HPF로 측정한 노이즈를 뺀다면 참값을 얻을 수 있다. 이에 대한 결과는 아래의 그림과 같다.

참고

칼만 필터는 어렵지 않아 - 김성필 저, 한빛아카데미