
무향 칼만 필터
EKF는 jacobian을 구하여 비선형 함수를 선형화시켜 칼만 필터의 큰 틀을 유지했다. 이와 반대로 UKF의 핵심은 선형화 과정을 생략해버리는 것이다. 이로 인해 선형 모델의 부정확성으로 인한 시스템이 발산하는 문제를 해결할 수 있는 것이 가장 큰 장점이다. 그렇다면 선형화 과정을 생략해버린다는 것은 어떤 방식으로 문제를 해결하는 것일까? 이에 대해 답을 하자면 선형화를 통한 근사화 대신 샘플링을 통한 근사화 전략을 택한다. 시스템을 대표하는 몇 개의 샘플을 이용해 상태변수와 오차 공분산의 예측값을 구한다는 것이다. 아래의 그림이 이를 잘 설명해준다.
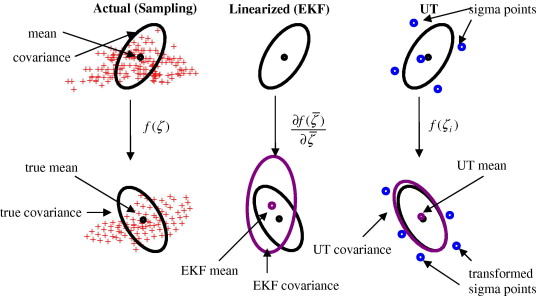
위의 그림에서 세번째에 위치한 그림을 살펴보자. 상대적으로 위에 있는 그림은 직전 시각()의 상태를 나타내고, 아래에 있는 그림은 현재 시각()을 나타낸다. 이전의 EKF에서 예측 단계는 1.1 ~ 1.3과 같이 수행되었다.
1.1
1.2
1.3
UKF에서는 시각 에서 상태변수 의 추정값 ()과 오차 공분산()을 나타내는 몇 개의 대표 데이터 ( 또는 Sigma Points)가 존재한다고 가정한다. 참고로 상태변수는 다음과 같은 정규분포를 따른다.
현재시각()에서 추정값과 오차 공분산의 예측값(, )은 시그마 포인트들을 시스템 모델로 변환한 데이터 ())로 부터 구할 수 있다. 이러한 변환을 Unscented Transfrom이라고 칭한다. 이처럼 상태 변수와 오차 공분산의 예측값을 시스템 모델식으로부터 직접 계산하는 대신(jacobian을 구하는 대신) 몇개의 대표값인 Sigma point를 선정하여 이 값의 변환 데이터로부터 간접적으로 구하는 것이 UKF의 핵심이다.
알고리즘
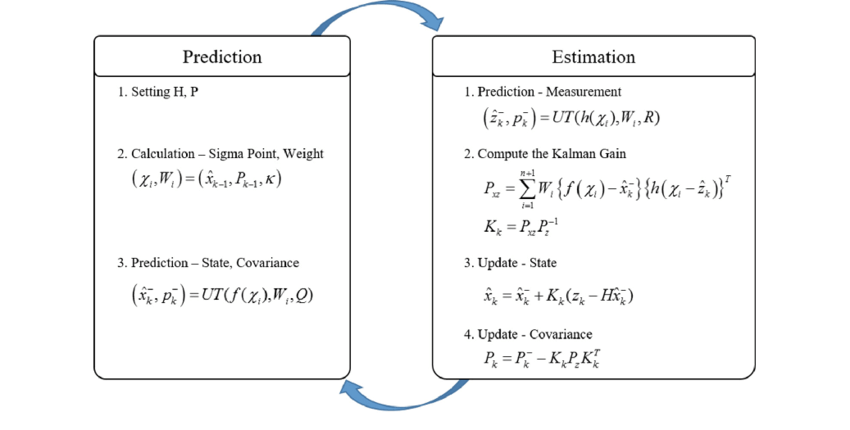
1) 가장 먼저 직전 시간의 추정값(과 오차 공분산을 대표하는 Sigma point와 Weight(가중치)를 선정한다.
2) 현재 시간에서의 상태변수와 오차 공분사의 예측값을 구한다. 예측값을 구하기 위해 시스템 모델 를 사용하여 계산을 수행하지 않고 Sigma point와 UT를 통해 간접적으로 계산한다.
3) 측정값의 예측값()과 측정값의 오차 공분산()을 구한다. 이값은 Kalman gain을 구하는데 쓰이게 된다. 2단계와 마찬가지로 측정값의 예측값을 시스템 모델()로부터 구하지 않고 UT를 통해서 간접적으로 계산한다.
4) Kalman gain을 계산한다. 이에 필요한 상태변수 ()와 측정값()의 공분산 행렬()을 계산한다. 마찬가지로 UT의 개념을 활용한다.
5) 와 측정값의 오차 공분산()의 역행렬을 곱해 Kalman gain을 계산하고 추정값과 오차 공분산을 업데이트한다.
Unscented Transform(UT)
평균이 이고, 분산이 인 정규분포를 따르는 상태변수 를 고려해보자.
에 대해 다음과 같은 Sigma point()와 가중치()를 정의한다. 선택된 Sigma point는 각각 가중치를 가지고 있으며, 가중치의 합은 1이 된다.
여기서 는 다음과 같은 행렬 의 행벡터이고, 는 임의의 상수이다. 특히, 는 sigma point가 평균으로부터 얼마나 떨어져 있는지를 조절하는 parameter이다.
2.1
Unscented Transform에서 sigma point는 상태 변수의 확률 분포를 대표하는 샘플 데이터에 해당된다. 또한, 가중치는 평균과 공분산을 계산할 때 각 sigma point의 비중을 결정하는 상수이다. 이에 따라 sigma point와 가중치는 다음과 같은 정규분포 특성을 만족한다.
3.1
3.2
3.1의 경우 sigma point의 가중 평균이 의 원래 평균인 과 동일하다는 의미이다. 3.2의 경우 sigma point의 가중 공분산은 의 공분산과 동일하다는 것이다. 즉, 개의 sigma point와 가중치만 있으면 의 평균과 공분산을 나타낼 수 있다는 것을 의미한다. 이 개념을 확장하여 의 평균과 공분산은 다음과 같이 구할 수 있다.
4.1
4.2
이는 위에서 보았던 그림과 동일한 의미를 지닌다.
코드
아래의 코드는 상태변수 의 sigma point를 구하는 함수이다.
function [Xi, W] = SigmaPoints(xm, P, kappa)
n = numel(xm); % 배열에 포함된 요소의 갯수 반환
Xi = zeros(n, 2*n+1); % simga points = Xi의 열
W = zeros(2*n+1, 1);
Xi(:, 1) = xm;
W(1) = kappa / (n+kappa);
U = chol((n+kappa)*P); % cholesky 분해를 수행
for k=1:n
Xi(:, k+1) = xm + U(k, :)';
W(k+1) = 1 / (2 * (n+kappa));
end
for k=1:n
Xi(:, n+k+1) = xm - U(k, :)';
W(n+k+1) = 1 / (2 * (n+kappa));
end다음은 예측값을 구하기 위해 Unscented transform을 수행하는 함수이다.
function [xm, xcov] = UT(Xi, W, noiseCov)
[n, kmax] = size(Xi);
xm = 0;
for k=1:kmax
xm = xm + W(k) * Xi(:, k);
end
xcov = zeros(n, n);
for k=1:kmax
xcov = xcov + W(k) * (Xi(:, k) - xm) * (Xi(:, k) - xm)';
end
xcov = xcov + noiseCov;예제1 - 레이더 추적 📡
시스템의 상태변수를 다음과 같이 정의한다.
시스템 모델을 정의한다.
5.1
5.2
이 시스템에 대해서 UKF를 적용해보자.
function [pos, vel, alt] = RadarUKF(z, dt)
%
%
persistent Q R
persistent x P
persistent n m
persistent firstRun
if isempty(firstRun)
Q = [ 0.01 0 0;
0 0.01 0;
0 0 0.01 ];
R = 100;
x = [0 90 1100]';
P = 100*eye(3);
n = 3;
m = 1;
firstRun = 1;
end
[Xi, W] = SigmaPoints(x, P, 0); %상태변수 x에 대한 시그마 포인트와 가중치를 구함
fXi = zeros(n, 2*n+1);
for k = 1:2*n+1
fXi(:, k) = fx(Xi(:,k), dt); % 시그마포인트를 f(x)에 대입
end
[xp, Pp] = UT(fXi, W, Q); % 변환된 시그마 포인트 획득, 평균(예측값)과 공분산을 구함
%norm(xp - fx(x, dt))
hXi = zeros(m, 2*n+1);
for k = 1:2*n+1
hXi(:, k) = hx(fXi(:,k));
end
[zp, Pz] = UT(hXi, W, R); % 측정값의 평균(예측값)과 공분산을 구함
%norm(zp - hx(xp))
Pxz = zeros(n, m);
for k = 1:2*n+1
Pxz = Pxz + W(k)*(fXi(:, k) - xp)*(hXi(:, k) - zp)'; % 칼만이득 계산을 위한 x와z의 공분산을 구함
end
K = Pxz*inv(Pz); % 칼만 이득 계산
x = xp + K*(z - zp); % 추정값
P = Pp - K*Pz*K'; % 공분산 값
pos = x(1);
vel = x(2);
alt = x(3);
%------------------------------
function xp = fx(x, dt)
%
%
A = eye(3) + dt*[ 0 1 0;
0 0 0;
0 0 0 ];
xp = A*x;
%------------------------------
function yp = hx(x)
%
%
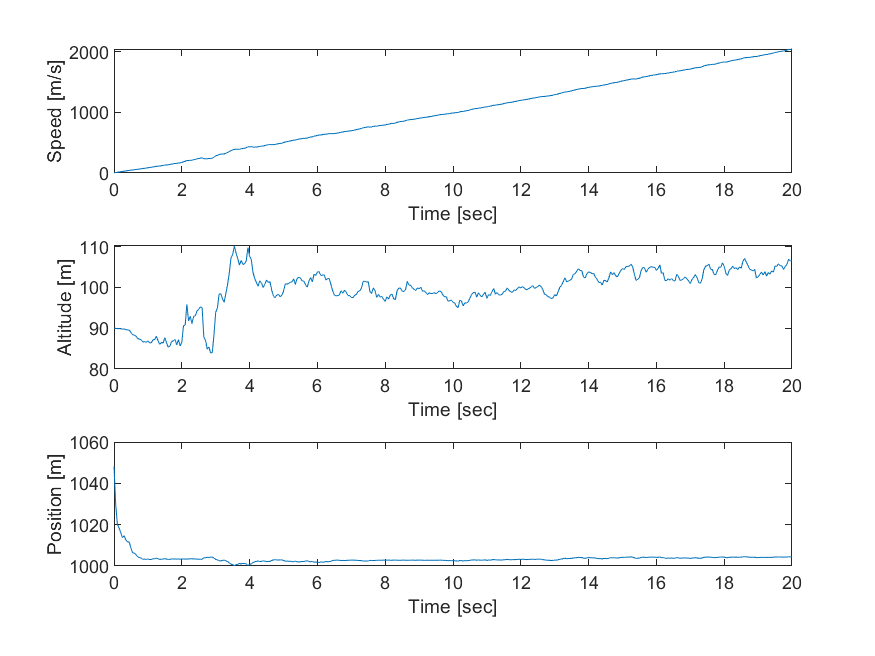
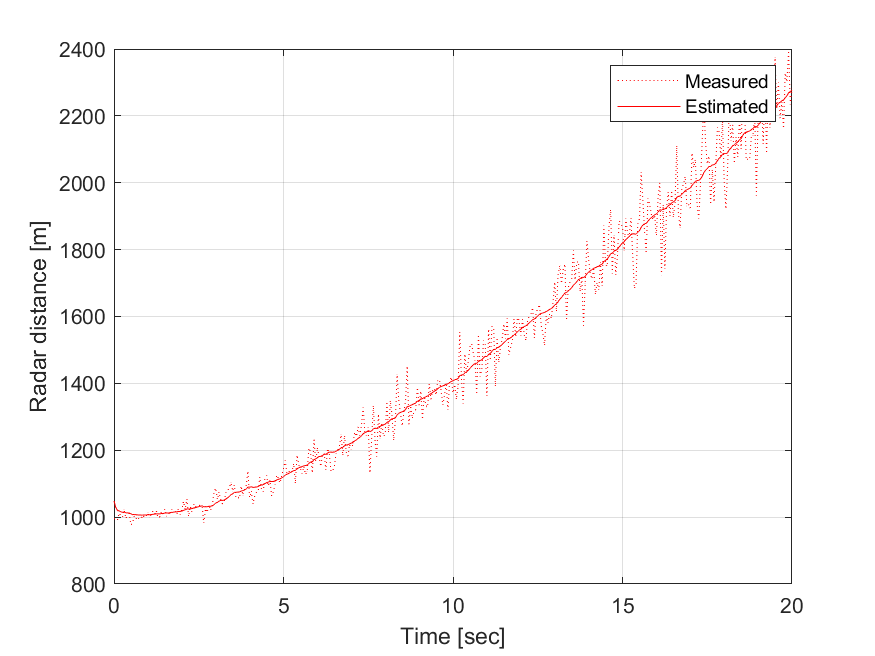
yp = sqrt(x(1)^2 + x(3)^2);예제1 - 레이더 추적 결과 📡
예제2 - 자이로, 가속도 센서 융합 🚁
시스템의 상태변수를 다음과 같이 정의한다.
시스템 모델은 다음과 같이 정의한다.
6.1
가속도 센서로는 yaw를 얻을 수 없으므로 측정 모델을 다음과 같이 설정할 수 있다.
위에서 작성한 SigmaPoints함수와 UT함수를 그대로 활용한다.
function [phi, theta, psi] = EulerUKF(z, rates, dt)
persistent Q R
persistent x_hat P
persistent n m
persistent firstRun
if isempty(firstRun)
% system noise
Q = [0.0001, 0, 0;
0, 0.0001, 0;
0, 0, 1];
% measurement noise
R = [10, 0;
0, 10];
x_hat = [0, 0, 0]'; % initial state variable(roll=0, pitch=0, yaw=0)
P = eye(3); % initial covariance
n = 3;
m = 2;
firstRun = 1;
end
[Xi, W] = SigmaPoints(x_hat, P, 0);
fXi = zeros(n, 2*n+1);
for k = 1:2*n+1
fXi(:, k) = fx(Xi(:, k), rates, dt);
end
[xp, Pp] = UT(fXi, W, Q);
hXi = zeros(m, 2*n+1);
for k = 1:2*n+1
hXi(:, k) = hx(fXi(:,k));
end
[zp, Pz] = UT(hXi, W, R);
Pxz = zeros(n, m);
for k = 1:2*n+1
Pxz = Pxz + W(k)*(fXi(:, k) - xp)*(hXi(:, k) - zp)';
end
K = Pxz*inv(Pz);
x_hat = xp + K*(z - zp);
P = Pp - K*Pz*K';
phi = x_hat(1);
theta = x_hat(2);
psi = x_hat(3);
function xp = fx(xhat, rates, dt)
phi = xhat(1);
theta = xhat(2);
p = rates(1);
q = rates(2);
r = rates(3);
xdot = zeros(3, 1);
xdot(1) = p + q*sin(phi)*tan(theta) + r*cos(phi)*tan(theta);
xdot(2) = q*cos(phi) - r*sin(phi);
xdot(3) = q*sin(phi)*sec(theta) + r*cos(phi)*sec(theta);
xp = xhat + xdot*dt;
function yp = hx(x)
yp(1) = x(1);
yp(2) = x(2);자이로, 가속도 센서 융합 결과 🚁
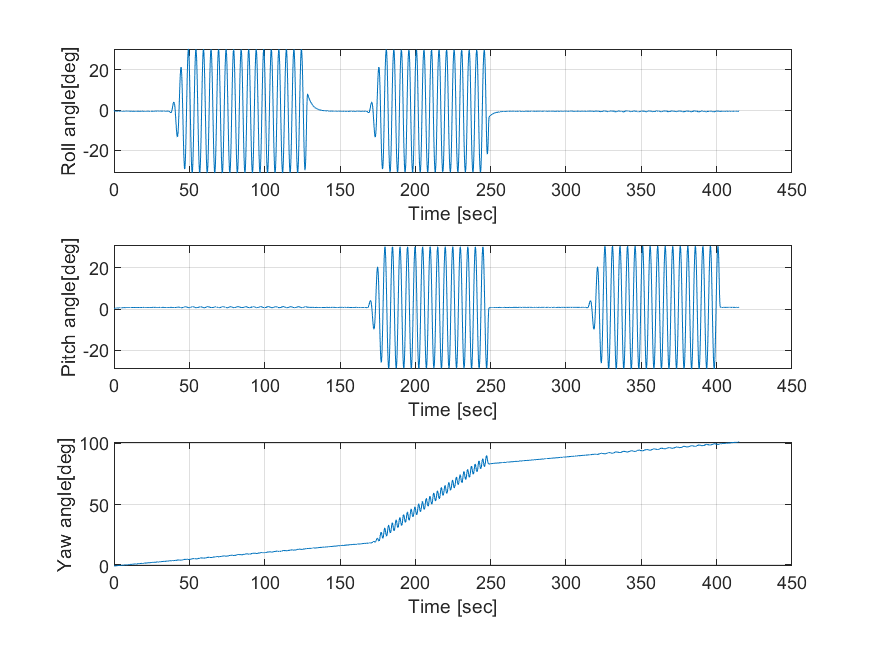
결과를 보면 알 수 있듯이 이전의 EKF를 적용한 결과와 거의 동일하며 비선형 시스템에 칼만 필터를 적용할 때 고려해야 할 점은 다음과 같다.
1) jacobian을 쉽게 구할 수 있다. EKF 사용
2) jacobian을 구할 수 없으며, EKF가 발산(선형화 모델은 기준점 근처에서만 실제 시스템과 비슷한 특성을 보이기 때문)할 염려가 있다. UKF 사용
참고
- [SLAM] Unscented Kalman Filter(UKF)
- 칼만 필터는 어렵지 않아 - 김성필 저, 한빛아카데미
