LSTM (Long Short Term Memory)

soup1997·2023년 3월 1일

Deep Learning LSTM RNN Time Series

딥러닝 모델

목록 보기

1/2

RNN(Recurrent Neural Network)

순환 신경망(Recurrent neural network, RNN)은 인공 신경망의 한 종류로, 유닛간의 연결이 순환적 구조를 갖는 특징을 갖고 있다.

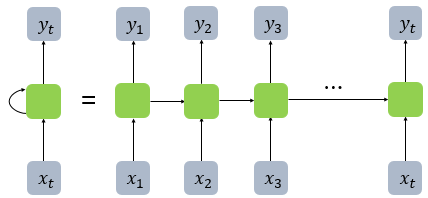
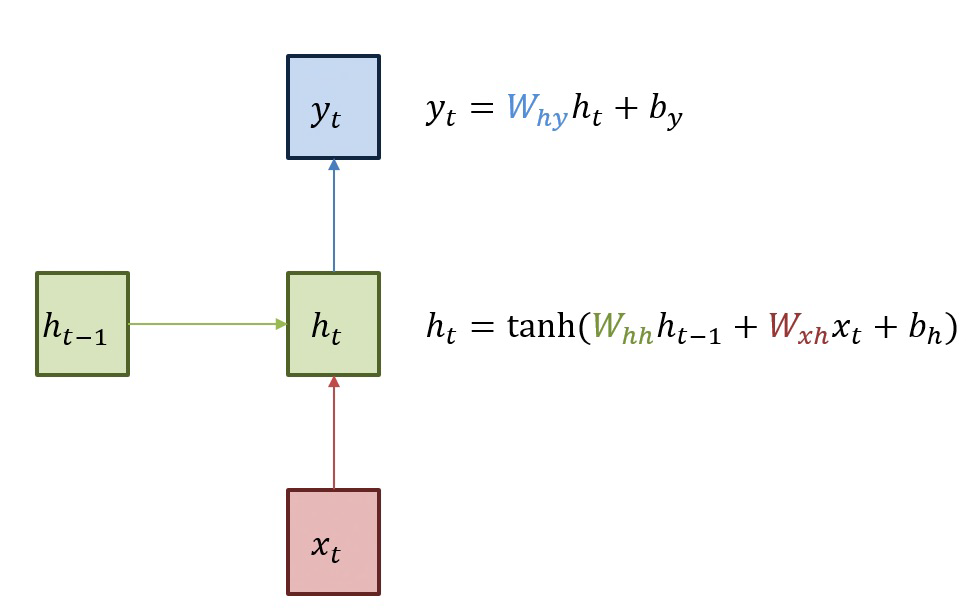
전통적인 neural network는 이전에 일어난 사건을 바탕으로 나중에 일어나는 사건을 생각하지 못한다. RNN은 이러한 신경망과 달리 은닉층의 노드에서 활성화 함수를 통해 나온 결과값을 출력층 방향으로도 보내면서, 다시 은닉층 노드의 다음 계산의 입력으로 보내는 특징을 가지고 있다. 메모리 셀이 출력층 다음 시점의 $t+1$ 의 자신에게 보내는 값을 hidden state라고 칭한다. $t$ 시점의 메모리 셀은 $t-1$ 시점의 메모리 셀이 보낸 은닉 상태값을 $t$ 시점의 은닉 상태 계산을 위한 입력값으로 사용된다. 이러한 RNN의 체인처럼 이어지는 성질은 입력데이터가 sequence나 iteration 객체 형태로 이어지는 것을 의미한다. 즉, 시계열 데이터(time series)에 최적인 neural network이다.

RNN의 한계

RNN의 가장 큰 단점은 시간 격차(time step)가 늘어날수록 학습정보를 계속 이어나가면 성능이 매우 떨어지게 된다는 것이다. 이에 대해 자세히 설명하자면 관련정보와 그 정보를 사용하는 지점사이 거리가 멀 경우 역전파시 gradient가 소멸되어 parameter들을 업데이트 할 수 없다는 것이다. 이를 vanishing problem이라고 칭한다. 따라서 RNN은 비교적 짧은 sequence에 대해서만 효과를 보인다. 이를 보완하기 위해 LSTM은 RNN의 은닉상태, hidden state에 셀 상태, cell state를 추가하였다.

LSTM (Long Short Term Memory)

순환 신경망은 추가적인 저장공간을 가질 수 있다. 이 저장공간이 그래프의 형태를 가짐으로써 시간 지연의 기능을 하거나 피드백 루프를 가질 수도 있다. 이와 같은 저장공간을 게이트된 상태(gated state) 또는 게이트된 메모리(gated memory)라고 하며, LSTM과 게이트 순환 유닛(GRU)이 이를 응용하는 대표적인 예시이다.

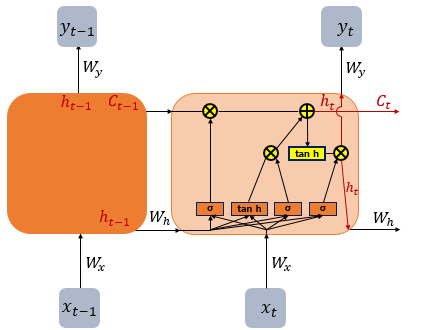
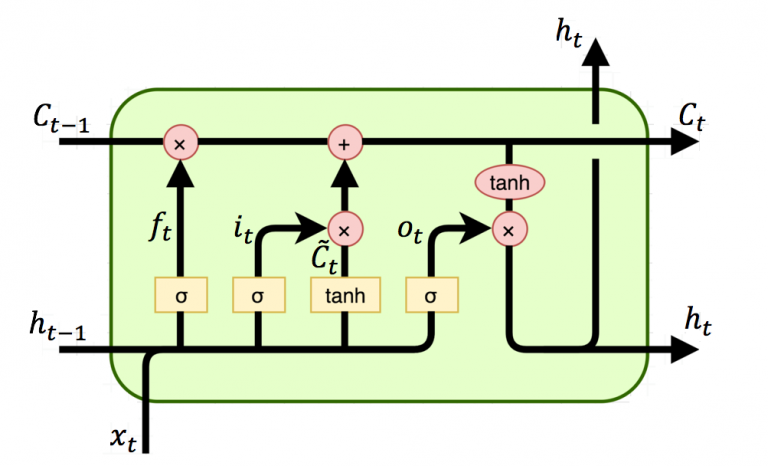
위의 그림에서 t시점의 cell state인 $C_t$ 를 표현하고 있다. LSTM은 RNN과 달리 긴 sequence의 입력을 처리하는데 뛰어난 성능을 보인다. 이러한 cell state $C_t$ 는 Gate라고 불리는 구조에 의해 제어되며 이는 데이터가 전달되거나 삭제되는 구조를 일컫는다.

진행 절차

Input Gate Layer

$i_t=\sigma(W_{xi}x_t+W_{hi}h_{t-1}+b_{i})$
$g_t=\tanh(W_{xg}x_t+W_{hg}h_{t-1}+b_{g})$

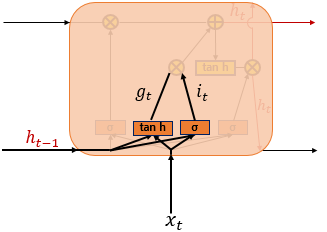
입력 게이트는 현재 정보를 기억하기 위한 게이트이다. $\sigma$ 를 통하여 나온 결과인 $i_t$ 는 0~1 범위의 값, $\tanh$ 를 통하여 나온 결과인 $g_t$ 는 -1~1 범위의 값을 가지게 된다. 이 두 값을 가지고 이번 스텝에 선택된 기억할 정보의 양을 정하게 된다.

Forget Gate Layer

$f_t=\sigma(W_{xf}x_t+W_{hf}h_{t-1}+b_{f})$

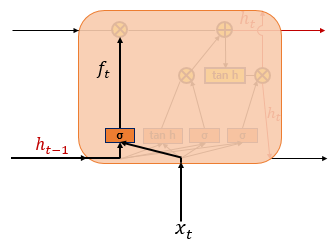
삭제 게이트는 기억을 삭제하기 위한 게이트이다. $\sigma$ 를 통하여 나온 결과인 $f_t$ 는 0~1 범위의 값을 가지게 되는데, 이 값이 삭제과정을 거친 정보의 양이다. 0에 가까울수록 이전 정보가 많이 삭제된 것이고 1에 가까울수록 정보를 유지하고 있는 것이다. 위의 두 게이트를 토대로 셀 상태를 구하게 된다.

Cell State Layer(장기 상태)

$C_t=f_t\odot C_{t-1}+i_t\odot g_t$

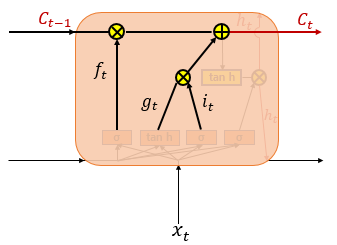
입력 게이트의 결과 값인 $i_t$ 와 $g_t$ , 삭제 게이트의 결과 값인 $f_t$ 를 입력받아 셀 상태인 $C_t$ 를 구하게 된다. 현재 시점의 $t$ 의 셀 상태인 $C_t$ 는 다음 $t+1$ 시점의 LSTM 셀로 넘겨진다. 만약 $f_t$ 가 0이 된다면 이전 시점의 셀 상태값인 $C_{t-1}$ 은 현재 시점의 셀 상태값을 결정하기 위한 영향력이 0이 되면서, 오직 입력 게이트의 결과만이 현재 시점의 셀 상태값 $C_t$ 를 결정하게 된다. 반대도 이와 같다. 따라서 결론적으로 각각 삭제 게이트는 이전 시점의 입력을 얼마나 반영하느냐를 나타내며입력 게이트는 현재 시점의 입력을 얼마나 반영하느냐를 나타내는 척도이다.

Output Gate Layer(단기 상태)

$o_t=\sigma(W_{xo}x_t+W_{ho}h_{t-1}+b_{o})$
$h_t=o_t\odot\tanh(C_t)$

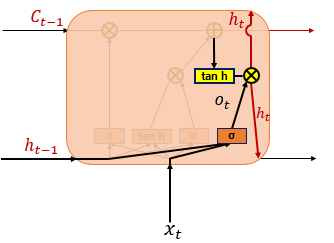
은닉 상태(단기 상태) $h_t$ 는 장기 상태의 값 $C_t$ 가 $\tanh$ 를 지나며 -1~1사이의 값을 가지게 된다. $h_t$ 는 출력층으로 향하여 $y_t$ 를 구하게 되며 동시에 다음 셀의 연산을 위해 입력된다.

Pytorch에서의 사용 (LSTMCell)

Pytorch에서 LSTMCell의 파라미터는 다음과 같다. 각각의 파라미터는 다음과 같은 의미를 지닌다.
torch.nn.LSTMCell(input_size, hidden_size, bias=True, device=None, dtype=None)

Parameter	설명
input_size	입력으로 주어지는 데이터의 feature의 갯수
hidden_size	hidden state $h$ 의 벡터 크기
bias	수식에서 $b$ 에 해당하는 편향(bias)값, default는 True

예제

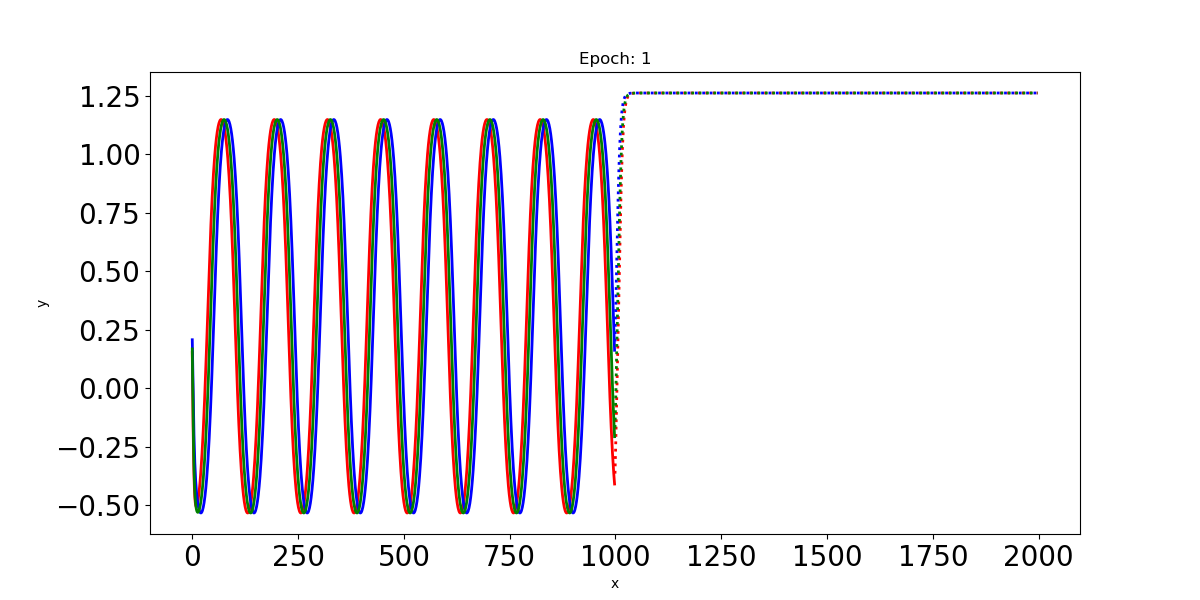
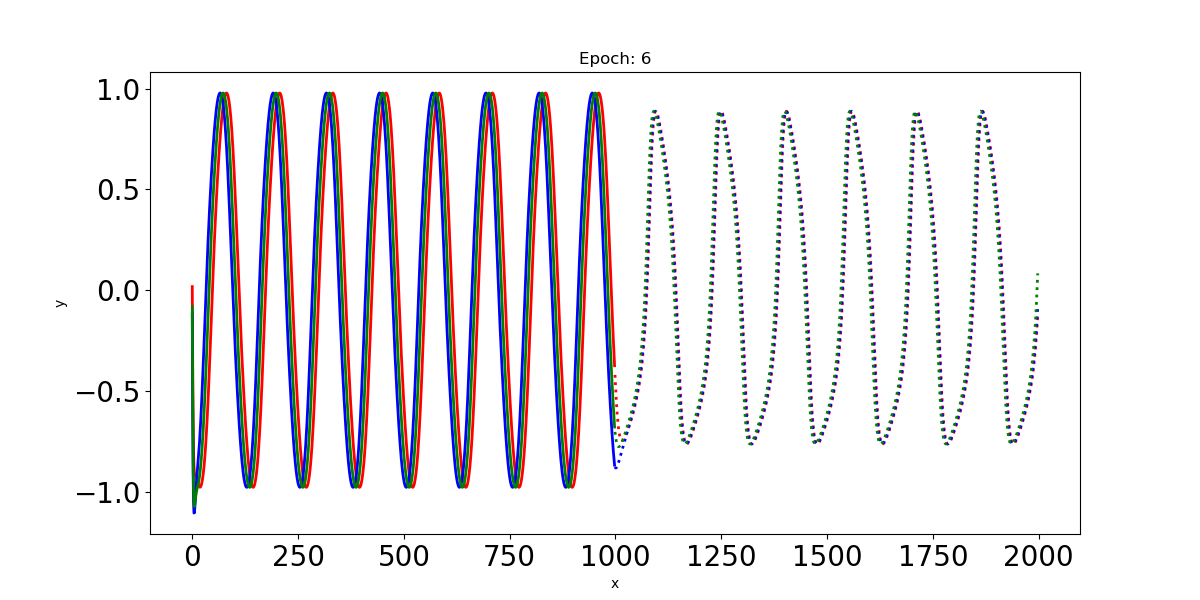
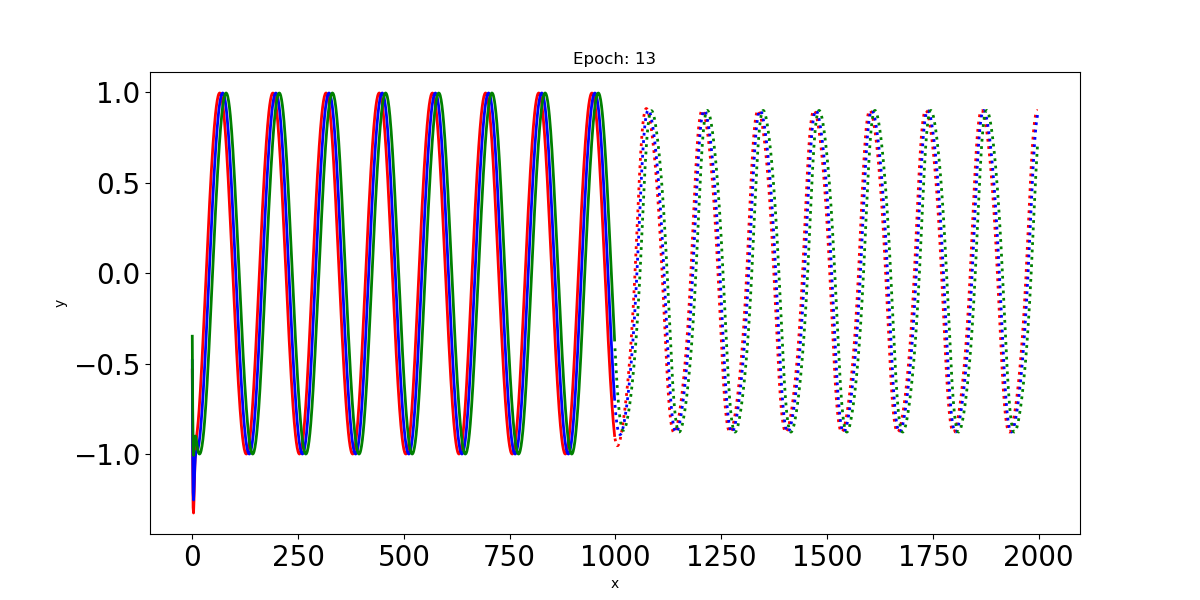
이 예제에서 Input인 사인파 입력신호는 최대 t=0:1000까지의 time step을 가지고 있다. 이 입력신호를 LSTM에 통과시켜 t=1000:2000까지의 time step에 대한 파형을 예측한다.

import numpy as np
import torch
import torch.nn as nn
import torch.optim as optim
from torch.utils.data import DataLoader, TensorDataset
import matplotlib.pyplot as plt

N = 100
L = 1000
T = 20

# =========================
# Create Input Signal
x = np.empty((N, L), dtype=np.float32)
x[:] = np.array(range(L)) + np.random.randint(-4*T, 4*T, N).reshape(N, 1)
y = np.sin(x/1.0/T).astype(np.float32)

plt.figure(figsize=(10, 8))
plt.title('Sine Wave')
plt.xlabel('x')
plt.ylabel('y')
plt.xticks(fontsize=20)
plt.yticks(fontsize=20)
plt.plot(np.arange(x.shape[1]), y[0, :], 'r', linewidth=2.0)
#plt.show()
# =========================

class LSTM(nn.Module):
    def __init__(self, n_hidden=51):
        super(LSTM, self).__init__()
        self.n_hidden = n_hidden

        # lstm1, lstm2, linear
        self.lstm1 = nn.LSTMCell(input_size=1, hidden_size=self.n_hidden)
        self.lstm2 = nn.LSTMCell(
            input_size=self.n_hidden, hidden_size=self.n_hidden)
        self.linear = nn.Linear(in_features=self.n_hidden, out_features=1)

    def forward(self, x, future=0):
        outputs = []
        n_samples = x.size(0)

        h_t = torch.zeros(n_samples, self.n_hidden, dtype=torch.float32)
        c_t = torch.zeros(n_samples, self.n_hidden, dtype=torch.float32)
        h_t2 = torch.zeros(n_samples, self.n_hidden, dtype=torch.float32)
        c_t2 = torch.zeros(n_samples, self.n_hidden, dtype=torch.float32)

        for input_t in x.split(1, dim=1):
            # N, 1
            h_t, c_t = self.lstm1(input_t, (h_t, c_t))
            h_t2, c_t2 = self.lstm2(h_t, (h_t2, c_t2))
            output = self.linear(h_t2)
            outputs.append(output)

        for _ in range(future):
            h_t, c_t = self.lstm1(output, (h_t, c_t))
            h_t2, c_t2 = self.lstm2(h_t, (h_t2, c_t2))
            output = self.linear(h_t2)
            outputs.append(output)

        outputs = torch.cat(outputs, dim=1)
        return outputs


if __name__ == '__main__':
    device = torch.device('cuda:0' if torch.cuda.is_available() else 'cpu')

    '''
    DataLoader 는 사용하고자 하는 모델을 초기화 하고 훈련 루프가 시작되기 전에 위치하는 것이 일반적이다. 
    데이터 정규화를 위한 mean 과 std 값, 그리고 batch_size, shuffle 과 같은 옵션은 
    상황에 맞게 configuration 하면 되겠다.
    '''
    # y = 100, 1000
    train_input = torch.from_numpy(y[3:, :-1])  # 97, 999
    train_target = torch.from_numpy(y[3:, 1:])  # 97, 999
    train_loader = DataLoader(TensorDataset(train_input, train_target),
                              batch_size=1,
                              shuffle=True)

    test_input = torch.from_numpy(y[:3, :-1])  # 3, 999
    test_target = torch.from_numpy(y[:3, 1:])  # 3, 999
    test_loader = DataLoader(TensorDataset(test_input, test_target),
                             batch_size=3,
                             shuffle=True)

    model = LSTM().to(device)
    criterion = nn.MSELoss().to(device)

    optimizer = optim.LBFGS(model.parameters(), lr=0.05)  # Limited-memory BFGS

    epochs = 13

    train_input, train_target = next(iter(train_loader))
    print("train input.shape: {}, train target.shape: {}".format(
        train_input.shape, train_target.shape))

    test_input, test_target = next(iter(test_loader))
    print("test input.shape: {}, test target.shape: {}".format(
        train_input.shape, train_target.shape))

    for epoch in range(epochs):
        print('Epoch: {}'.format(epoch))
        
        for train_input, train_target in train_loader:
            train_input, train_target = train_input.to(
                device), train_target.to(device)

            def closure():
                optimizer.zero_grad()
                out = model(train_input)
                loss = criterion(out, train_target)
                print('Train loss: {}'.format(loss.item()))
                loss.backward()
                return loss   
        optimizer.step(closure)

        with torch.no_grad():  # Gradient 추적 X, 매 Epoch마다 평가해보기
            for test_input, test_target in test_loader:
                test_input, test_target = test_input.to(
                    device), test_target.to(device)

                future = 1000
                pred = model(test_input, future=future)
                loss = criterion(pred[:, :-future], test_target)
                print("Test loss: {}".format(loss.item()))
                y = pred.detach().numpy()
		
        # =========================
        # 매 Epoch마다 결과 값 Plot
        plt.figure(figsize=(12, 6))
        plt.title('Epoch: {}'.format(epoch+1))
        plt.xlabel('x')
        plt.ylabel('y')
        plt.xticks(fontsize=20)
        plt.yticks(fontsize=20)

        n = train_input.shape[1]  # 999

        plt.plot(np.arange(n), y[0][:n], 'r', linewidth=2.0)
        plt.plot(np.arange(n, n+future), y[0][n:], 'r:', linewidth=2.0)

        plt.plot(np.arange(n), y[1][:n], 'b', linewidth=2.0)
        plt.plot(np.arange(n, n+future), y[1][n:], 'b:', linewidth=2.0)

        plt.plot(np.arange(n), y[2][:n], 'g', linewidth=2.0)
        plt.plot(np.arange(n, n+future), y[2][n:], 'g:', linewidth=2.0)

        plt.savefig("Prediction %d.png" % epoch)
        plt.close()
        # =========================