선형 칼만 필터

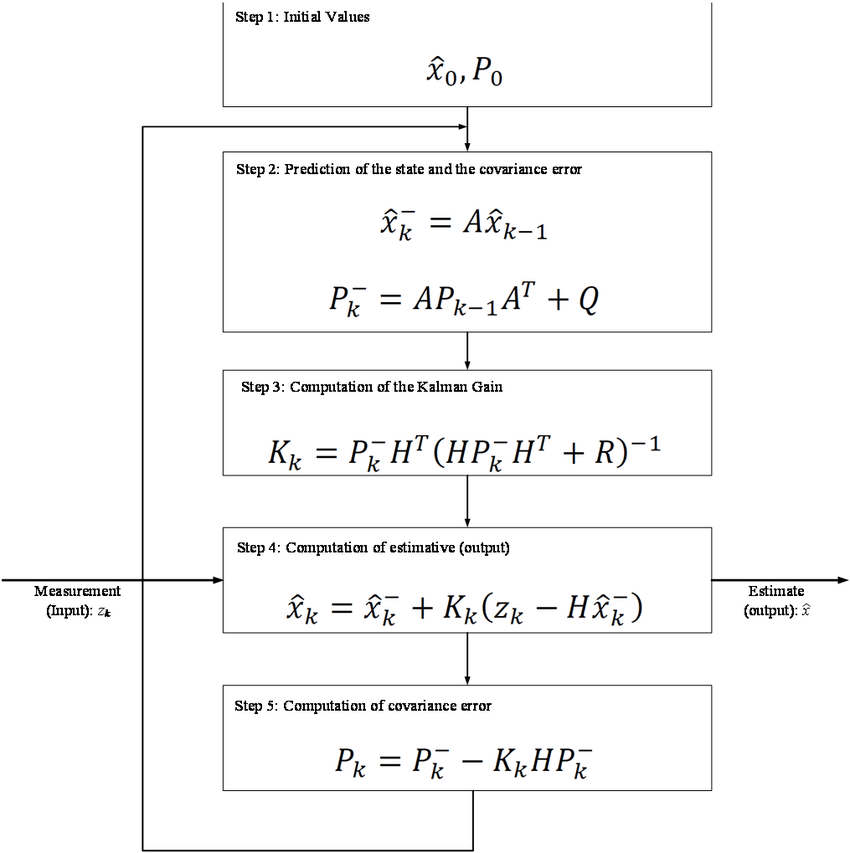
Sensor measurement input인 $z_k$가 칼만 필터로 입력되어 처리된 후 Estimated output인 $\hat{x}$을 출력하는 것이 여느 재귀 필터와 마찬가지로 칼만 필터의 목적이라고 할 수 있다.

목적	변수
외부 입력	$z_k$
최종 출력	$\hat{x}_k$
시스템 모델	$A, H, Q, R$
예측값 및 기타 파라미터	$\hat{x}_k^-, P_k^-, P_k, K_k$

시스템 모델과 관련된 네개의 변수 $A, H, Q, R$은 칼만필터의 목적에 따라 사용자가 사전에 확정한다. 따라서 사용자가 조정할 수 있는 변수는 시스템 모델과 관련된 네개의 변수뿐이다. 따라서 이러한 시스템 모델이 실제 시스템과 가까워질수록 전체 시스템의 성능이 결정된다.

시스템 모델

시스템 모델은 다루는 문제를 수학적으로 표현해 놓은 것을 말한다. 칼만 필터는 다음과 선형 상태 모델을 대상으로 한다.

$x_{k+1}=Ax_k+w_k$ (1.1)
$z_k=Hx_k+v_k$ (1.2)

위의 두식에서 모두 마지막에 +항이 추가되는 것을 확인할 수 있다. 이는 시스템 모델에 잡음이 포함되어 있다는 의미이다. (1.1)을 먼저 살펴보면 다음 스텝의 상태변수 $x_{k+1}$은 현재 스텝의 상태변수(State variable) $x_k$와 시스템 행렬 $A$의 행렬곱에 시스템 잡음인 $w_k$가 더해진 형태이다. (1.2)도 마찬가지로 센서 측정값인 $z_k$는 출력행렬인 $H$와 행렬곱에 측정 잡음인 $v_k$가 더해진 형태이다. 이와같이 칼만 필터에서는 잡음이 중요한 역할을 하며 특히나 모든 잡음을 Gaussian distribution으로 가정한다. 특히, 평균이 0인 $N(0, \sigma^2)$의 확률적 분포를 가진다고 가정한다. 이에 따라 칼만 필터 알고리즘의 수식을 살펴보면 다음과 같다.

$\hat{x}_{k}^-=A\hat{x}_{k-1}$ (2.1)
$\hat{x}_k=\hat{x}_{k}^-+K_k(z_k-H\hat{x}_{k}^-)$ (2.2)

위의 선형 상태 모델식과 칼만필터의 추정값 계산식을 비교해보면 잡음 항($w_k,v_k$)이 제외되어 있는 점을 제외하고는 시스템 모델과 연관되어 있음을 알 수 있다. 또한 State variable인 $x_k$는 다음과 같은 분포를 가지게 된다. 이는 오차의 공분산인 $P_k$가 (3.2)와 같이 정의되기 때문이다.

$x_k \sim N(\hat{x}_k, P_k)$ (3.1)
$P_k=E[(x_k-\hat{x}_k)(x_k-\hat{x}_k)^T]$ (3.2)
cf) $Var(X)=E[(X-E[X])^2]=E[X^2]-(E[X])^2$

즉 오차의 공분산은 추정 오차의 제곱을 평균한 값을 의미한다는 것이다. 따라서 오차의 공분산은 추정값의 오차를 나타내는 척도로 사용되며 $P_k$가 증가하면 추정오차도 증가하는 비례관계를 가지고 있다.

잡음의 공분산

위에서 언급하였듯이 칼만 필터에서 잡음은 평균이 0인 정규분포를 따른다고 가정한다. 따라서 잡음의 분산값을 알 수 있다면 이를 시스템 모델의 파라미터로 이용할 수 있게된다. 따라서 칼만 필터는 상태 모델의 잡음을 다음과 같은 공분산 행렬로 표현한다.

$Q:w_k$(시스템 잡음)의 공분산 행렬, 대각 행렬
$R:v_k$(센서 측정 잡음)의 공분산 행렬, 대각 행렬

여기서 공분산 행렬은 변수의 분산으로 구성된 행렬로, 예를 들어 n개의 잡음 $w_1,w_2, \dots,w_n$이 있고 각 잡음의 분산은 $\sigma_1^2,\sigma_2^2,\dots,\sigma_n^2$이라고 할때 공분산 행렬은 다음과 같이 나타난다. $R$도 마찬가지로 나타낼 수 있다.

$Q= \begin{bmatrix} \sigma_1^2 & 0 & \cdots & 0 \\ 0 & \sigma_2^2 & \cdots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \cdots & \sigma_n^2 \end{bmatrix}$ (4.1)

추정 과정

행렬 $Q$와 $R$은 칼만 이득 계산식에서 이용된다. 칼만 이득을 계산하는 방법은 (5.1)과 같다.

$K_k=P_k^-H^T(HP_k^-H^T+R)^{-1}$ (5.1)

이 식에서 모든 변수가 스칼라라고 가정하면 칼만이득을 계산하는 방법은 다음과 같이 표현될 수 있다. 그리고 칼만 필터의 추정값은 위에서 언급했듯이 (6)와 같다.

$K_k=\frac{P_k^-H^T}{(HP_k^-H^T+R)}$ (6.1)
$\hat{x}_k=\hat{x}_{k}^-+K_k(z_k-H\hat{x}_{k}^-)$ (6.2)

칼만 이득에서 $R$이 커지면 칼만 이득은 작아지고, R이 작아지면 칼만 이득은 커진다. 이에 따라 추정값 계산에 측정값이 반영되는 비율도 달라지게 된다. 또한, 행렬 $Q$는 오차 공분산의 예측값 계산에 이용된다.

$P_{k+1}^-=AP_kA^T+Q$ (7.1)

행렬 $Q$가 커지면 오차 공분산 예측값도 커진다. 오차 공분산 예측값이 커지면 칼만 이득도 커짐을 알 수 있다. 이를 통해 결론적으로 칼만 필터에서는 추정값을 계산하는 가중치($K_k$)가 동일하지 않고 칼만 필터의 알고리즘에 따라 새로 계산된다.

예측 과정

$\hat{x}_k=\hat{x}_{k}^-+K_k(z_k-H\hat{x}_{k}^-)$ (8.1)
$\hat{x}_k=A\hat{x}_{k-1}+K_k(z_k-HA\hat{x}_{k-1})$ (8.2)

식 (8)에서 볼 수 있듯이 칼만 필터는 1차 저주파 통과 필터와 달리 추정값을 계산할 때 직전 추정값을 바로 쓰지 않고 예측 단계를 걸쳐서 추정값을 내는 것을 확인할 수 있다. 결론적으로 추정값의 성능에 크게 영향을 미치는 요인은 예측값의 정확성이며 예측단계에서 사용되는 시스템 모델인 $A, Q$가 결정적인 영향을 미치게 된다.

참고

칼만 필터는 어렵지 않아 - 김성필 저, 한빛아카데미