초간단 칼만 필터 예제

칼만 필터를 이용한 첫번째 예제는 '14V의 전압이 일정하게 출력되는 배터리의 노이즈를 제거'하는 것이다. 칼만 필터를 이용하기 위해서 가장 먼저 시스템 모델을 정의한다.

시스템 모델 설정

$x_{k+1} = x_k$ 1.1
$z_k=x_k+v_k$ 1.2
$x_0=14,v_k\sim N(0, 2^2)$

1.1을 먼저 살펴보자. DC배터리의 전압은 일정하게 유지되므로 이전 스텝의 상태변수와 다음 스텝의 상태변수가 같다. 또한 Measurement value인 $z_k$의 경우 State variable인 $x_k$와 Measurement noise인 $v_k$의 합으로 나타낼 수 있다. 이에 따라 칼만필터의 파라미터는 다음과 같이 정의된다.

$A=1$
$H=1$
$Q=0$
$R=4$

가장 먼저 $A$의 경우 2.1의 상태방정식에서 증명할 수 있다.

$x_{k+1}=Ax_k+w_k$ 2.1

2.1의 상태방정식과 1.1을 비교해보면 $A=1$이라는 사실을 알 수 있으며 또한 시스템 잡음인 $w_k$항이 존재하지 않으므로 $w_k=0$이다. 따라서 $Q$는 $w_k$의 공분산 행렬인데 이것이 존재하지 않으므로 0이되는 것을 알 수 있다. 두번째로 $H$의 경우 3.1의 식에서 확인할 수 있다.

$z_k=Hx_k+v_k$ 3.1

3.1과 1.2를 비교하면 마찬가지로 $H=1$이라는 것을 알 수 있으며 $R$의 경우 Measurement noise인 $v_k$의 공분산 행렬인데 $v_k\sim N(0, 2^2)$의 분포를 가지므로 이에 따라 스칼라 값인 $R=4$로 결정된다. 최종적으로 이를 확인하기 위해 칼만 필터의 알고리즘에 따라 초깃값을 다음과 같이 선정하였다.

$\hat{x}_0^- = 14$
$P_0^-=6$

알고리즘

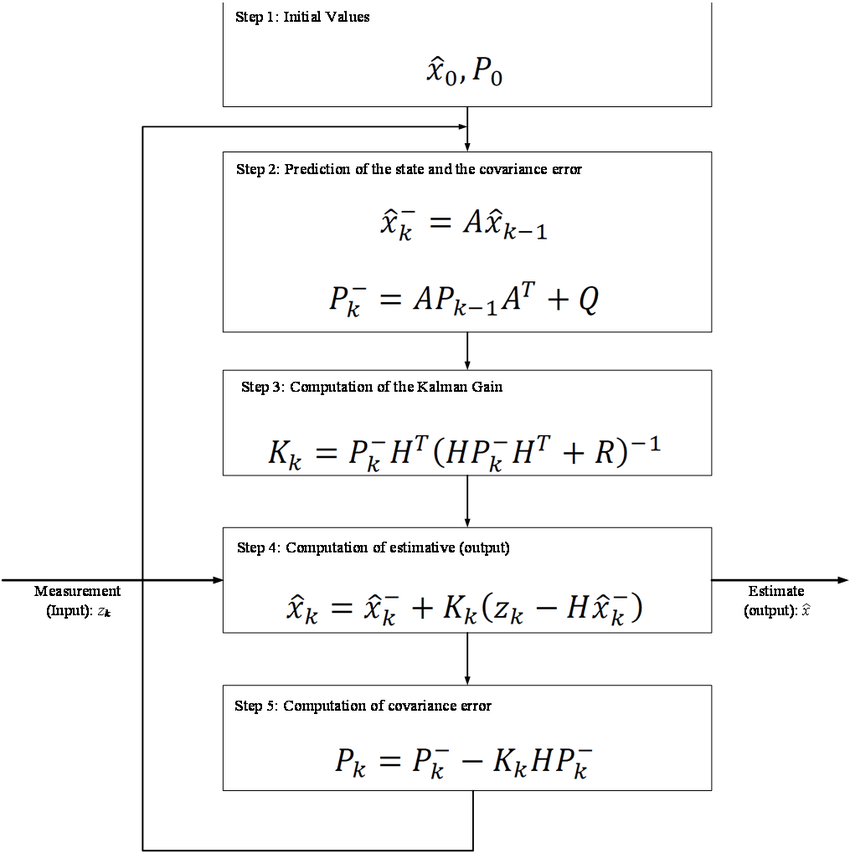
칼만 필터의 블록 다이어그램은 위의 사진과 같다. 이를 토대로 코드를 작성했다.

코드

function [volt, Px, K] = SimpleKalman(z)

%{
System Model

x_(k+1) = x_k (배터리의 전압이 일정하게 유지되므로 이전상태와 현재상태가 동일)
z_k = x_k + v_k (Measurement Value = State Variable + Measurement Noise)

x_0 = 14 (Initial State Value = 14)
v_k ~ N(0, 4) (Normal Distribution, mean = 0, variance = 4)

%}

persistent A H Q R
persistent x_hat P
persistent firstRun

if isempty(firstRun)
    A = 1;
    H = 1;

    Q = 0; % w_k(시스템 잡음)의 공분산 행렬(Diagonal Matrix)
    R = 4; % v_k(센서 측정 잡음)의 공분산 행렬(Diagonal Matrix)

    x_hat = 14; % x_0(Initial Value)
    P = 6; % P_0 (Initial Error Covariance)

    firstRun = 1;

end

% Prediction
x_pred = A * x_hat;
P_pred = A*P*A' + Q;

% Calculate Kalman Gain
K = (P_pred*H')/(H*P_pred*H' + R);

% Update
x_hat = x_pred + K*(z - H*x_pred);
P = P_pred - K*H*P_pred;

% return Estimated State Value & Error Covariance
volt = x_hat;
Px = P;

end

결과

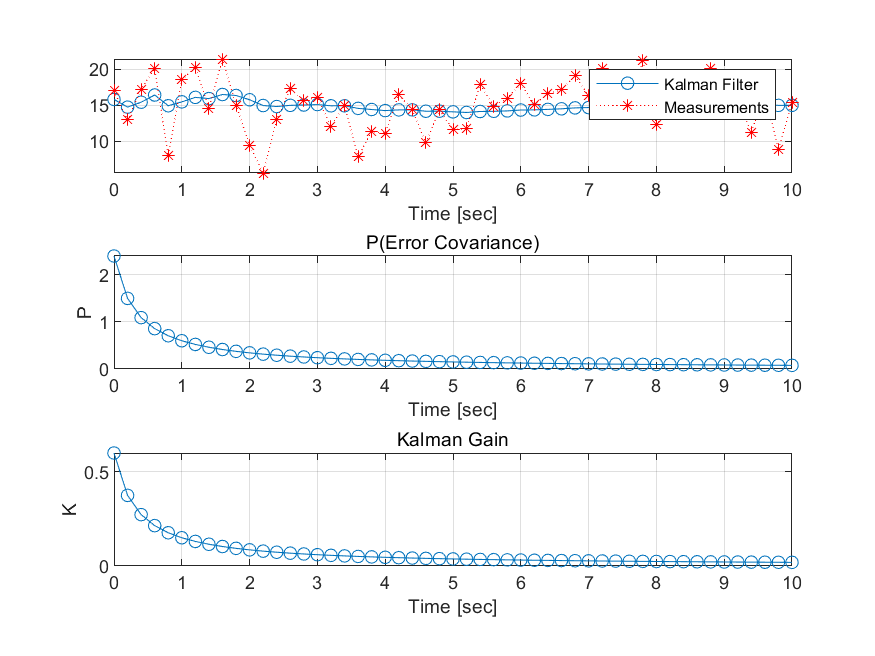
시간이 흘러감에 따라 효과적으로 노이즈를 제거하면서, 동시에 오차 공분산값인 $P$와 칼만 이득값인 $K$가 작아지는 것을 확인할 수 있다. 결론적으로 오차 공분산이 줄어든다는 것은 추정값의 오차가 감소하는 것을 의미한다. 또한, 칼만 이득이 작아짐에 따라 새로운 추정값인 $\hat{x}_k$는 예측값인 $K_k(z_k-H\hat{x}_k^-)$의 영향이 작아지고 이전 예측값 즉, $\hat{x}_k^-=A\hat{x}_{k-1}$의 영향이 커지게 된다. 결국 이전 추정값의 영향을 더 받게 된다는 의미이다.

참고

칼만 필터는 어렵지 않아 - 김성필 저, 한빛아카데미