저주파 통과 필터

이전에 포스트한 이동평균필터에는 명백한 한계가 존재한다. 이는 아래 수식으로 설명할 수 있다.

$\overline{x_k}=\frac{x_{k-n+1}+x_{k-n+2}+\dots+x_k}{n}$
$=\frac{1}{n}x_{k-n+1}+\frac{1}{n}x_{k-n+2} + \dots+\frac{1}{n}x_{k}$

즉, 이동평균 필터는 모든 데이터에 동일한 가중치인 $\frac{1}{n}$을 부여하기 때문에 가장 오래된 데이터와 가장 최신의 데이터를 같은 비중으로 평균에 반영한다는 명백한 단점이 존재한다. 저주파 통과필터는 이러한 단점에서 출발한다. 오래된 값일수록 가중치를 낮게 주고, 최신 값에는 높은 가중치를 주는 것이다. 1차 저주파 통과필터의 수식은 아래와 같다.

$\overline{x_k}=\alpha\overline{x_{k-1}}+(1-\alpha)x_k$

$\alpha$는 직관적으로 $0<\alpha<1$의 범위를 가지는 파라미터임을 알 수 있다. 또한, 저주파 통과필터의 $\overline{x_k}$는 평균이 아닌 추정 값(estimation value)이다. 오래된 값에 가중치를 낮게 부여하고 최신 값에는 높은 가중치를 부여한다고 했는데 이는 아래의 수식을 통해 확인할 수 있다.

$\overline{x_k}=\alpha\overline{x_{k-1}}+(1-\alpha)x_k$
$=\alpha^2\overline{x_{k-2}}+\alpha(1-\alpha) x_{k-1}+(1-\alpha)x_k$
$=\alpha^3\overline{x_{k-3}}+\alpha^2(1-\alpha)x_{k-2}+\alpha(1-\alpha) x_{k-1}+(1-\alpha)x_k$

특히나 계수의 크기를 판별해보면 다음과 같다.

$\alpha^2(1-\alpha)<\alpha(1-\alpha)<1-\alpha$

위의 부등식을 통해 이전 측정 데이터일수록 더 작은 계수가 곱해진다는 사실을 확인할 수 있다.

저주파 통과 필터 예제

function xlpf = LPF(x, alpha)

persistent prevX;
persistent firstRun;

if isempty(firstRun)
    prevX = x;

    firstRun = 1;
end

xlpf = alpha * prevX + (1-alpha) * x;

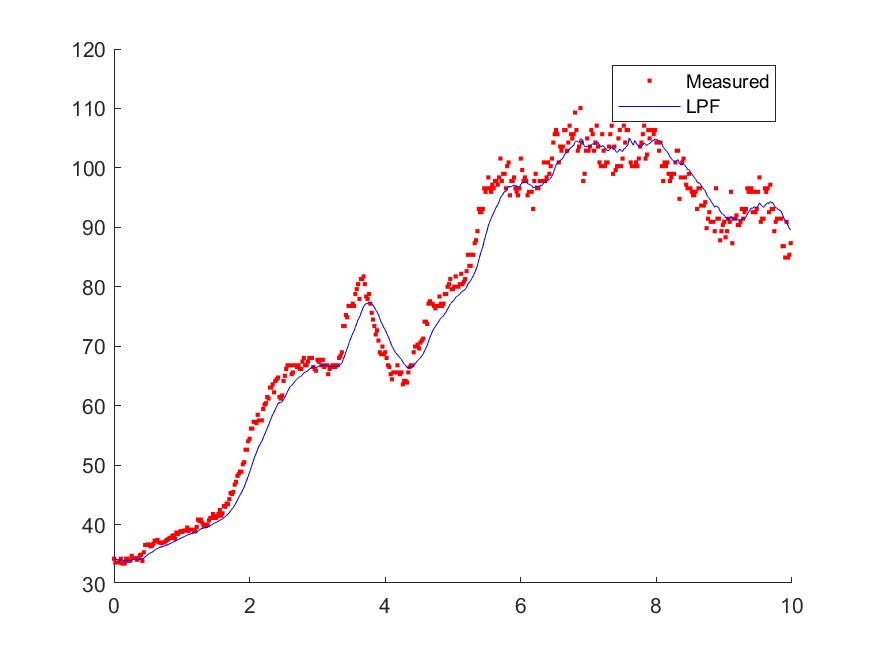
prevX = xlpf;

이동평균에 비해 시간 지연현상이 개선되었음을 확인할 수 있지만 이동평균의 파라미터인 $n$과 마찬가지로 $\alpha$값의 선정에 따라 필터의 지연현상, 잡음 제거 성능이 결정됨을 마찬가지로 확인할 수 있다. 추가적으로 $\alpha$가 작을수록 데이터 값을 잘 따라가지만 잡음제거 성능이 떨어진다. 이러한 tradeoff를 적절히 상충하는 파라미터 설정의 중요성에 대해 다시 복습할 수 있었다.

참고

칼만 필터는 어렵지 않아 - 김성필 저, 한빛아카데미