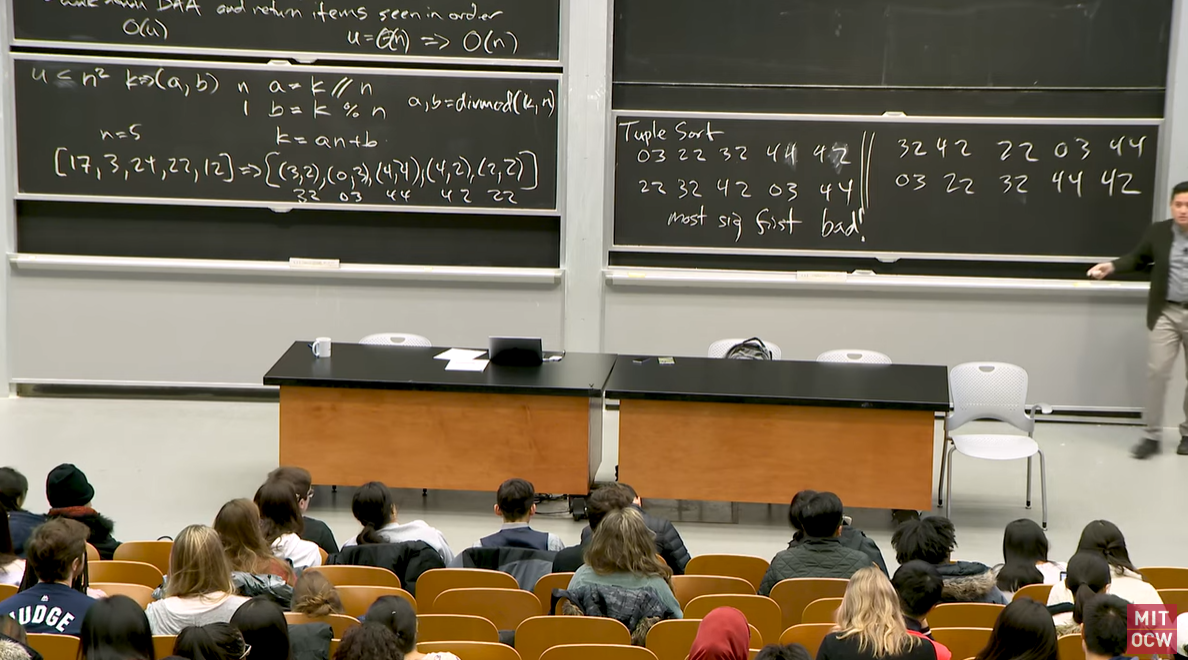
여기에 정리할 요약 노트의 원 강의는 MIT 6.006 Introduction to Algorithms, Spring 2020이다.
Direct Access Array Sort
Suppose u is small and all the keys are unique. Make a direct access array(O(u)), store each key in their respective indices(n * O(1)) and walk down the array and return the keys seen in order(O(u)). The whole process will take O(n+u), which is a linear time algorithm
What if u gets bigger, say, u is smaller than n squared. Decompose each item into two smaller numbers. For example, with k, you can get two smaller numbers a and b, a being k/n and b being k mod n. You can retrieve the k value later because you know k=an+b. For example, when you have a set of keys that go: [17, 3, 24, 22, 12], after the decomposition, you get a tuple of [(3,2), (0,3), (4,4), (4,2), (2,2)], or, [32, 03, 44, 42, 22]
Tuple Sort
When there are many factors you can base the sorting on, you first have to rearrange the factors in order of importance. In the example above, you would say a is more important than b in that a change in the value of a leads to a greater change the value of k.
Most significant first
First sort the tuple by a:
[03 22 32 44 42]
Then, sort it again by b:
[22 32 42 03 44] X
Least significant first
First sort the tuple by b:
[32 42 22 03 44]
Then, sort it again by a:
[03 22 32 42 44] O
As you can see, the tuple should be sorted by the least significant first. Also note that you should use stable sorting algorithm, meaning the outcome of the first sorting should remain intact unless effected by the sortings to follow. That is why the final outcome on the right is 03 22 32 42 44, not 03 22 32 44 42. You cannot use direct access array sort with the outcome because of possible duplicates(42 and 44 in this case)
Counting Sort
At each key K in the direct access array, we store a pointer to a chain. The chain should remain the same order in which the elements were put. Thus, the chain should be a sequence data structure
| 0 | 1 | 2 | 3 | 4 |
|---|---|---|---|---|
| 03 | 22 | 32 | 42 | |
| 44 |
To guarantee all the elements in every chain are sorted, you can combine tuple sort and counting sort, using counting sort as an auxiliary stable sorting algorithm. This also takes O(n+u) when k is equal to or less than n squared because u is n in this specific example and the maximum amount of a is n(when k=n squared). When k is increase to n cubed, you simply divide k into three digits(when you divide k with n, you will be left with n squared and this can again be divided into the combination of a and b)
Radix Sort
Break up integers(max size u) into a base-n tuple. The number of digits is log n of u. It is the same as tuple sort on digits using counting sort from least to most significant. It takes O(n + n log n U) as long as u is smaller than n to the power of c, c being any constant, making it a linear time algorithm
