DFT

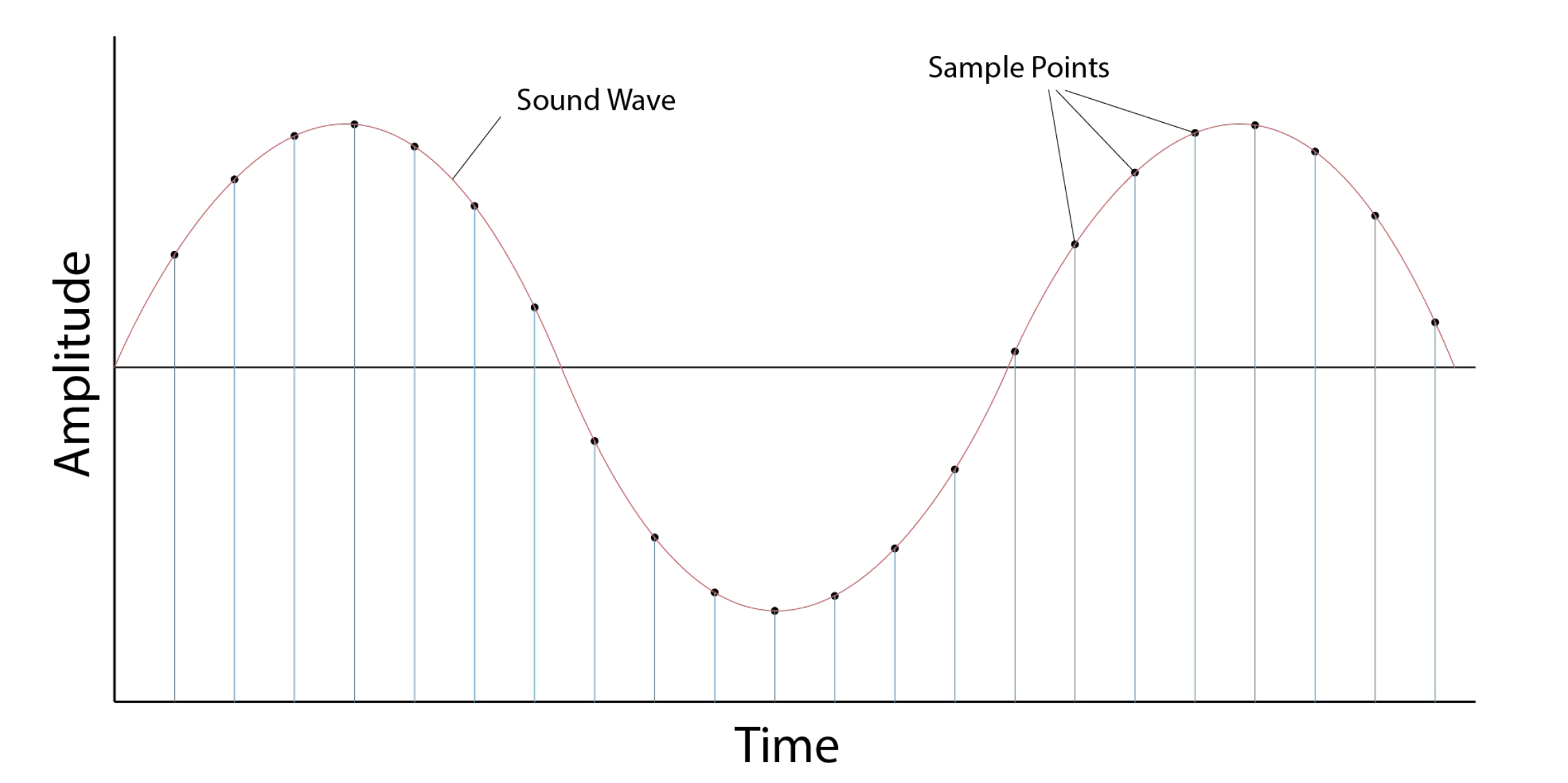
기계가 무한대의 푸리에 변환을 계산할 수 없다. 그래서 유한개로 적당히 쪼개서 계산한다는것이 DFT이다.

위 그림과 같이 time에 대해서 불연속적으로 잘라주자. 그러면

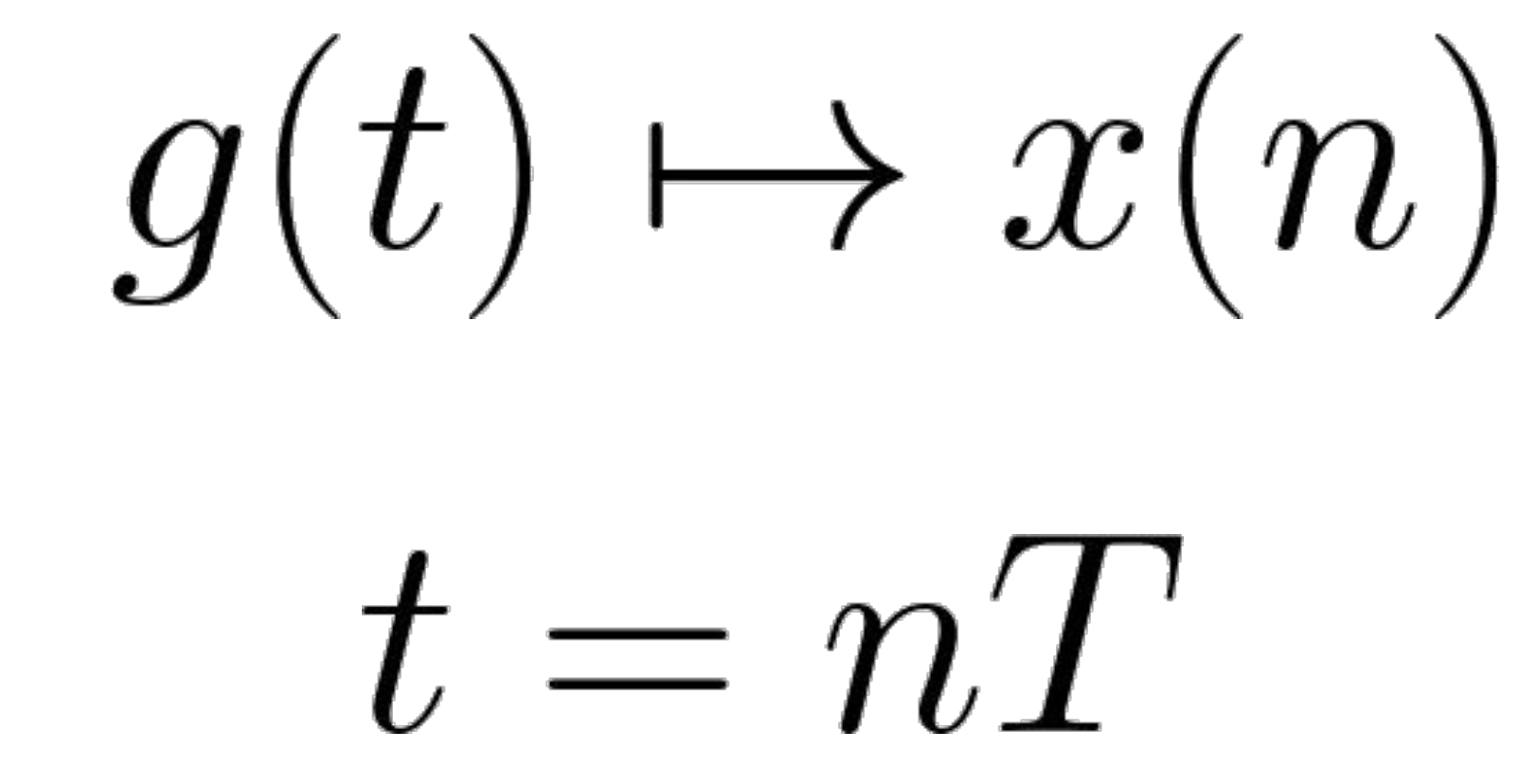
시간에 대한 푸리에 변환을 위와 같이 n에 대한 식으로 바꿀 수 있다.

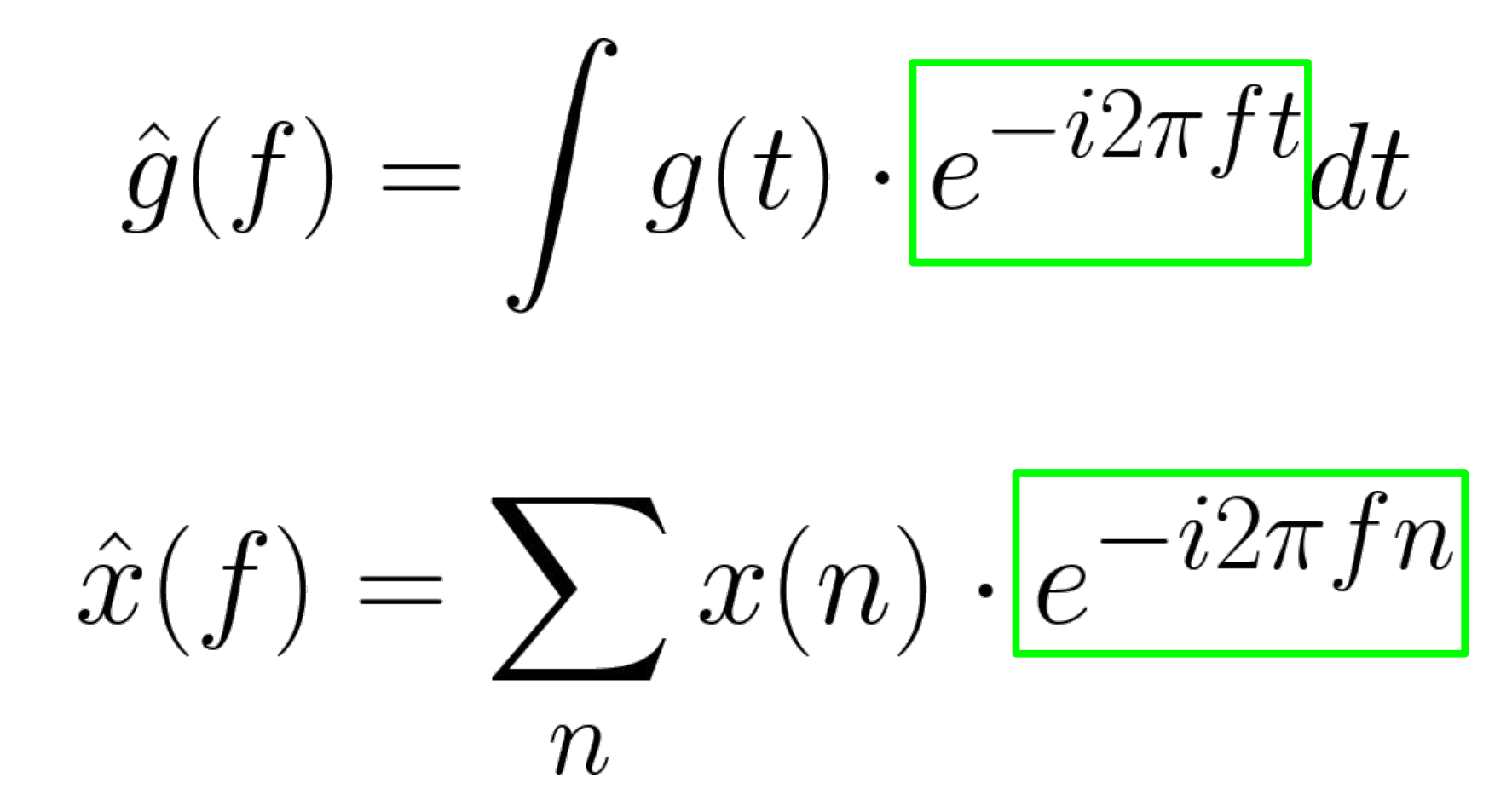
전체적으론 이렇게 이산적으로 n에 대한 식으로 바꿀 수 있다.

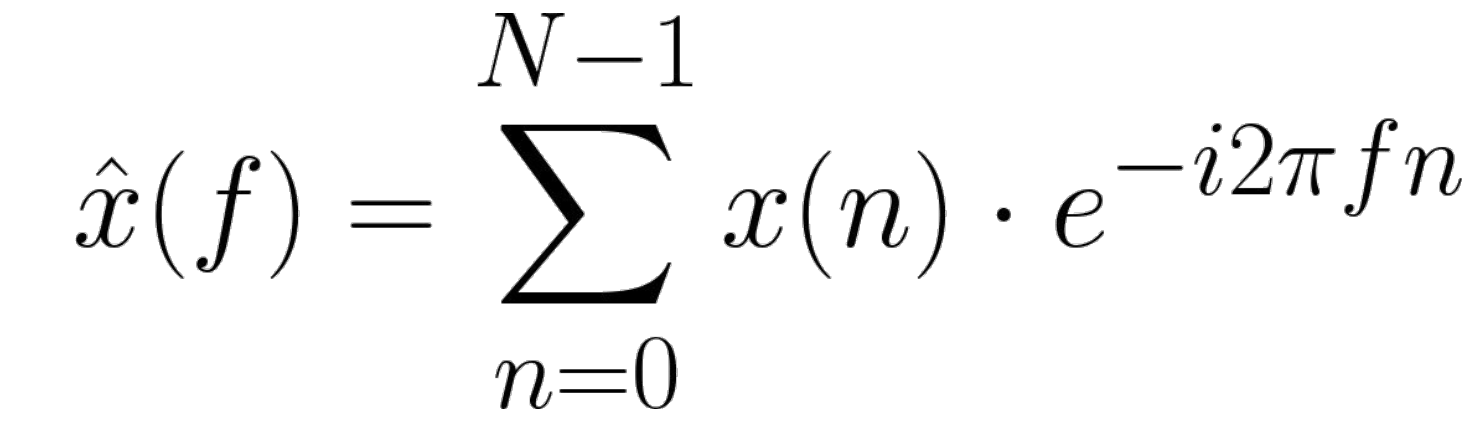
우리의 신호의 세기에 해당하는 계수는 위와 같이 구할 수 있다. e이 푸리에 변환에선 기저에 해당되는 데 식을 잘 들여다보면 유한한 기저 N개로 식을 표현하는 것을 알 수 있다.

그럼 우리가 해줘야되는건 전체 주파수의 특징을 특정 주파수로만 나타내야한다. 왜나면 푸리에 변환이 수많은 주파수에 가중치를 줘서 변환하는 건데 주파수 또한 불연속적으로 몇개만 써야지 컴퓨터가 계산가능하기 때문이다.

컴퓨터가 주파수를 표현하는게 sampling rate로 계산하기 때문에 주파수를 sampling rate와 관련있게 변환하자.

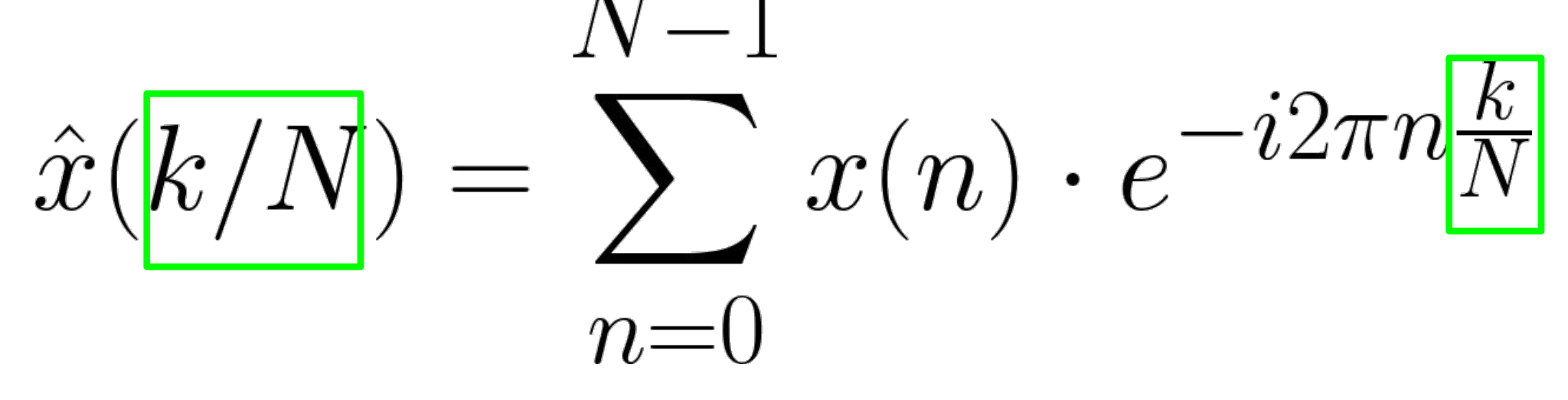
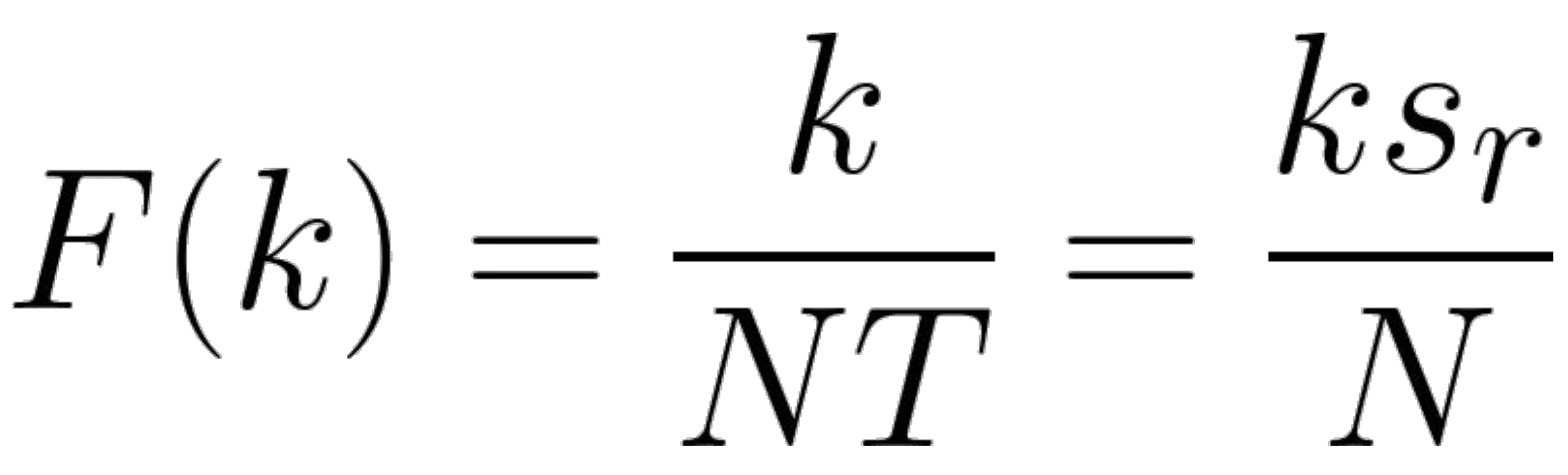
k/n 은 샘플링 레이트를 전체 간격으로 균일하게 나눈것으로 볼 수 있다.

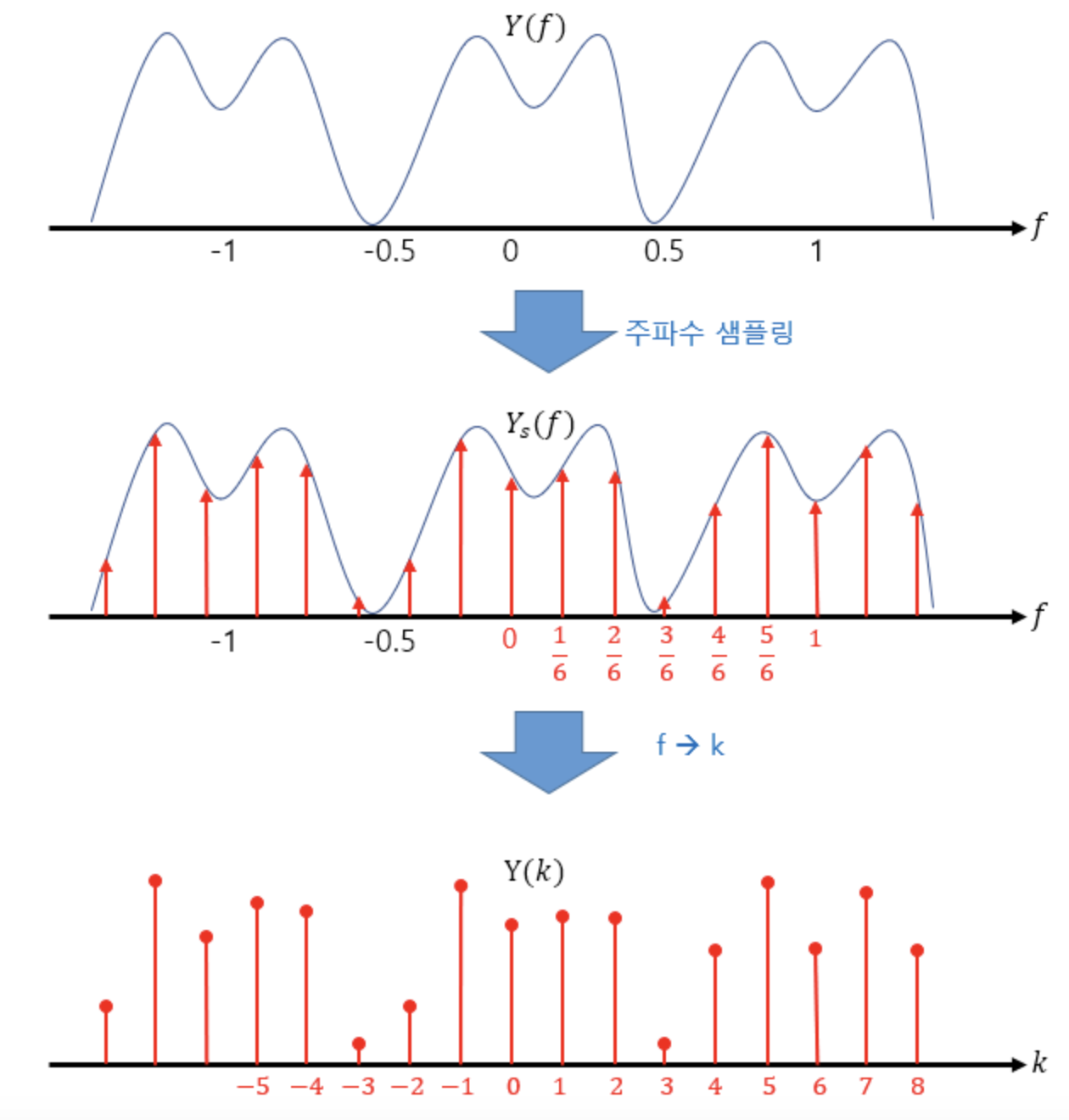
위 그림과 같이 샘플링 데이트에 대해서 균일하게 나눠서 몇가지 주파수에 대해서만 신호를 표현했다.

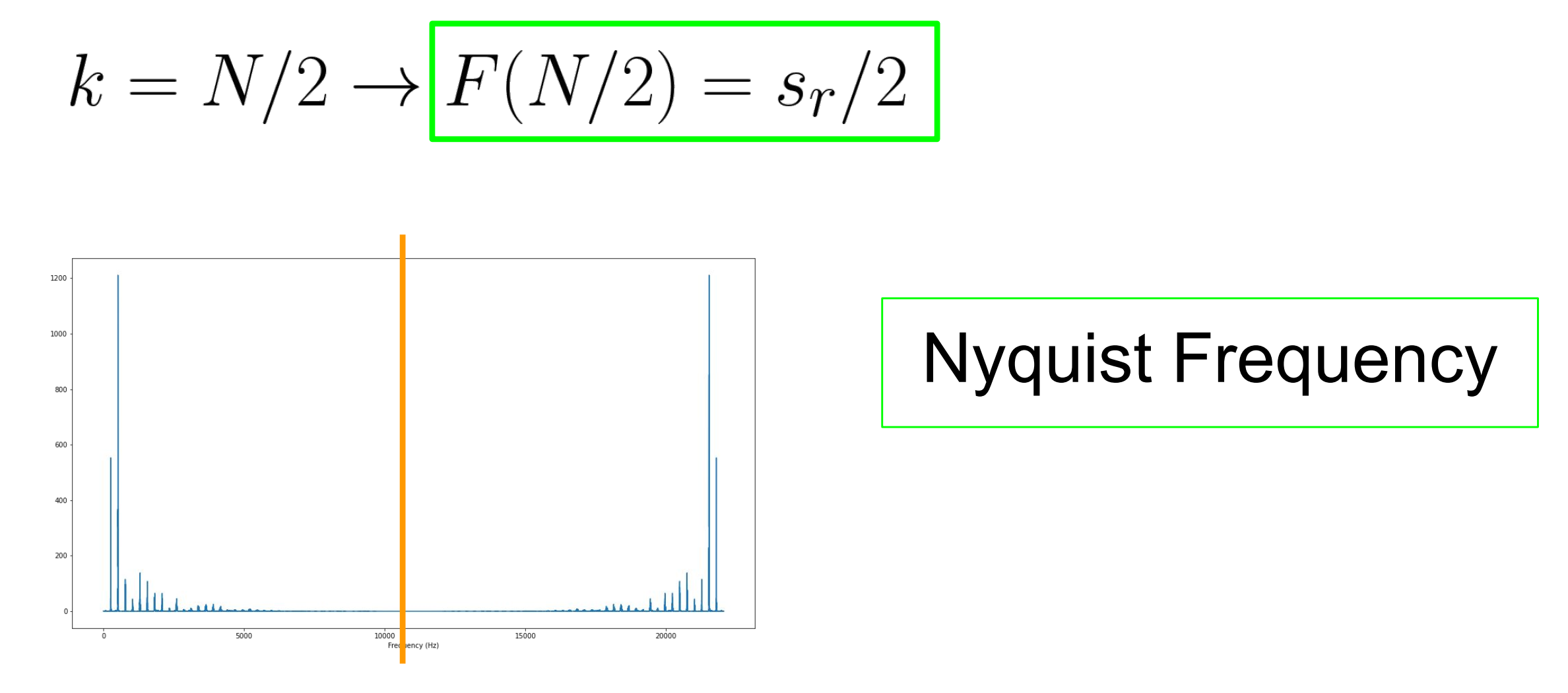
또 한 가지 중요한 성질은 위 DFT식이 오일러 공식에 의해서 표현되었지만 실제 물리적으로 음원은 실수 부분만 나타난다. 무슨 말이면

이 식에서 실수 부분인 코사인 부분만 현실세계에서 음원으로 표현되기 때문에 DFT의 계수는 샘플링 레이트의 절반 값에 대해서 대칭이다.

좀 더 자세히 설명해보면 DFT의 기저인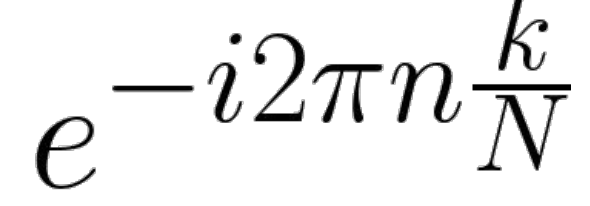

이 값을 오일러 방정식으로 표현하면

cos(x) - isin(x) 이때 x는 익스포텐셜 함수에 정의역을 그냥 퉁쳐서 x라고 뒀다.

파이에 대해서 대칭이라면

f(2$\pi$ - x) = f(x)를 만족해야 한다.

음원은 오일러 방정식에서 실수 부분만을 뜻하니 cos(2$\pi$ - x) = cos(x)를 만족해야한다.

만족하냐? 응 2$\pi$는 없어지고 cos(-x) = cos(x)여서 만족한다. 즉 $\pi$에 대해서 대칭이다.

따라서 위 DFT식에 오일러 공식의 실수부분이 파이에 대해서 대칭인데 파이에 해당하는 정의역 값이 샘플링 레이트의 절반 값이기 때문에

그래서 우리는 실질적으로 샘플링 레이트의 절반 값인 nyquistFrequency에 범위에서만 주파수의 특징을 잡고 그 뒤에 값은 버려도 된다.

DFT에서 원래 신호로 복귀할 때도 모든 신호의 정보가 nyquistFrequency안에 있기 때문에 DFT의 nyquistFrequency를 넘는 정보를 가지고 있어야만 원래 신호로 복귀할 수 있다.

librosa로 DFT 구현

일단 알고리즘으로 DFT를 구현하는 방법이 Fast Fourier Transform이다. 흔히 FFT라고 부르는 데 정말 중요한 알고리즘이지만 다음 기회에 포스팅하겠다.

일단 ipynb파일을 하나 만들어주자.

import os
import librosa
import matplotlib.pyplot as plt
import librosa.display
import IPython.display as ipd
import numpy as np

라이브러리 가져오고

beenzino = "/Users/seong-gyeongjun/Downloads/bugs_20230203160747/진절머리 (Feat. Okasian, Dok2)_빈지노_24_26 (5th Anniversary Remaster Edition).mp3"

파일 하나 경로 가져와서 객체로 만든다.

ipd.Audio(beenzino)

ipd로 맞는지 확인해주고

zino, sr = librosa.load(beenzino)

librosa로 로드해준다.

X = np.fft.fft(zino)
len(X)

numpy의 fft를 이용해서 DFT를 구해줄거다.

def plot_magnitude_spectrum(signal, sr, title, f_ratio=1):
    X = np.fft.fft(signal)
    X_mag = np.absolute(X)
    
    plt.figure(figsize=(18, 5))
    
    f = np.linspace(0, sr, len(X_mag))
    f_bins = int(len(X_mag)*f_ratio)  
    
    plt.plot(f[:f_bins], X_mag[:f_bins])
    plt.xlabel('Frequency (Hz)')
    plt.title(title)

그림을 그리는 함수를 하나 만들자. fft와 magnitude를 구해주고 주파수에 대한 f = np.linspace(0, sr, len(X_mag))을 구해주자.

f_bins = int(len(X_mag)*f_ratio)는 주파수에서 어떤 비율로 그릴것인가를 뜻한다. 예를 들어서 0.1이면 전체 주파수에 0.1만 가져와서 그리겠다는 뜻

plot_magnitude_spectrum(zino, sr, "zino", 1)

이걸 해주면

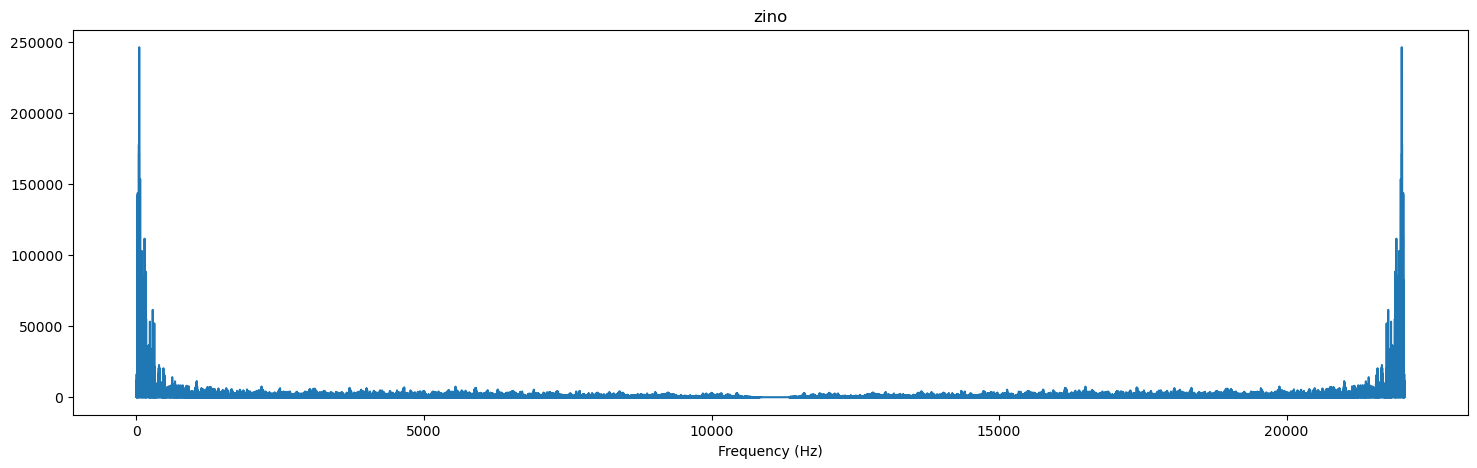
음원의 길이가 커서 저렇게 나왔는데 우리가 확인할건 중앙값에 대해 대칭이란것을 알 수 있다. 왜냐면 함수의 f_ratio를 1로 설정해서 모든 DFT에 대한 정보를 그렸기 때문이다. 이번엔 0.5로 해보면

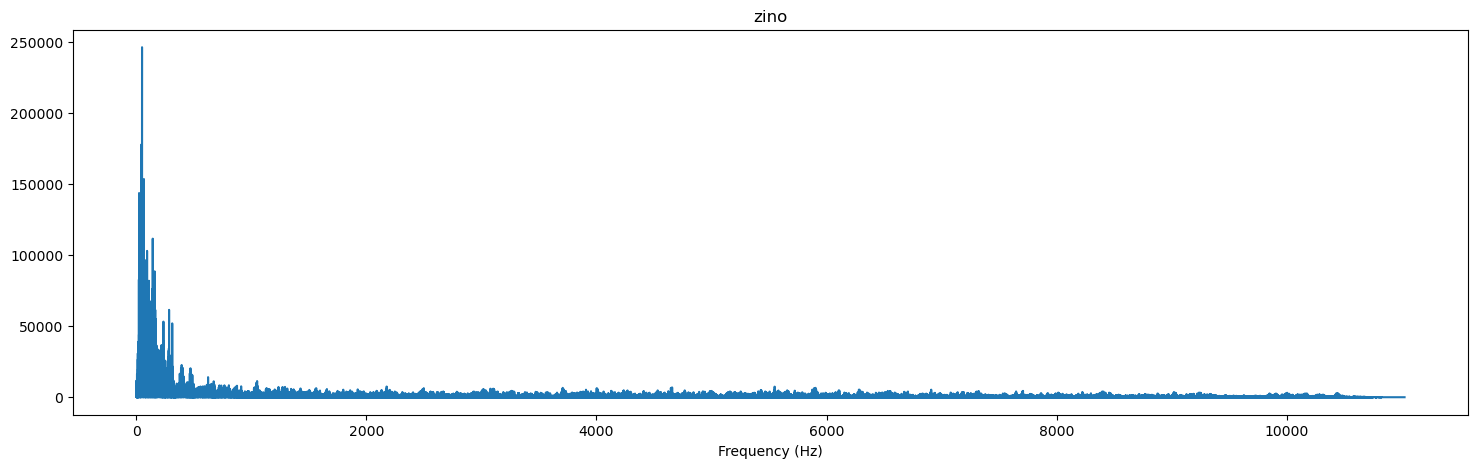
nyquist frequency까지 구할 수 있다. 우리가 필요한건 nyquist frequency까지의 그림이니 이걸 사용하면 된다.