Spectral leakage

구글에 한글로 된 자료가 없다 없어

한글로 된 유일한 자료가 위키인데 오해에 저렇게 박아놨다.

근데 영어로 된 자료를 여러개 봤는데 죄다 신호처리 박사들이랑 교수들이 나와서 spectral leakage가 이산 푸리에 변환에 의해 발생하고 창 함수로 완화할 수 있다고 하는 데 뭐가 맞는말인가?

웃긴게 박사들끼리 서로 멍청하다고 싸우고 있는데 비전공자는 참 곤란하다 이럴땐 뭐 내가 자료조사해서 그럴듯한쪽 의견 수용하는 게 정석이겠지

아주 아쉬운 부분이 신호처리란 분야는 수학을 사용하지 못하는 건가? 대부분의 설명이 장황하고 말로만 설명을 하고 있어서 아주 곤란한 부분이 있다.

그래도 유트브와 교재, 수식을 이용한 설명들을 종합해서 요약해보겠다.

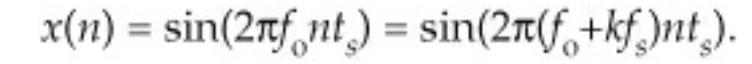
x(n)

이 문장은 샘플링 이론과 관련된 중요한 개념 중 하나인 "샘플링 주파수(fs)와 원래 신호의 주파수(fo) 사이의 관계"를 설명하고 있습니다. 여기서 fs는 초당 샘플 수를 의미하며, fo는 원래 신호의 주파수입니다. k는 양수나 음수가 될 수 있는 정수입니다.

이 문장의 핵심은 어떤 신호를 샘플링할 때, 그 신호의 주파수가 fo인 경우와 (fo+kfs)인 경우를 구분할 수 없다는 것을 의미합니다. 여기서 kfs는 샘플링 주파수의 정수배를 의미합니다. 이 현상은 "에일리어싱(Aliasing)" 또는 "주파수 중첩"으로 알려져 있습니다.

예를 들어, 만약 샘플링 주파수가 1000Hz(fs=1000)이고, 우리가 샘플링하는 신호의 주파수가 300Hz(fo=300)라면, k=1일 때 (fo+kfs)는 1300Hz가 됩니다. 이론적으로 300Hz 신호와 1300Hz 신호를 1000Hz로 샘플링하면, 샘플링된 데이터는 구별할 수 없게 됩니다. 이는 두 신호가 같은 샘플링 포인트에서 서로 유사한 값을 가지기 때문입니다.

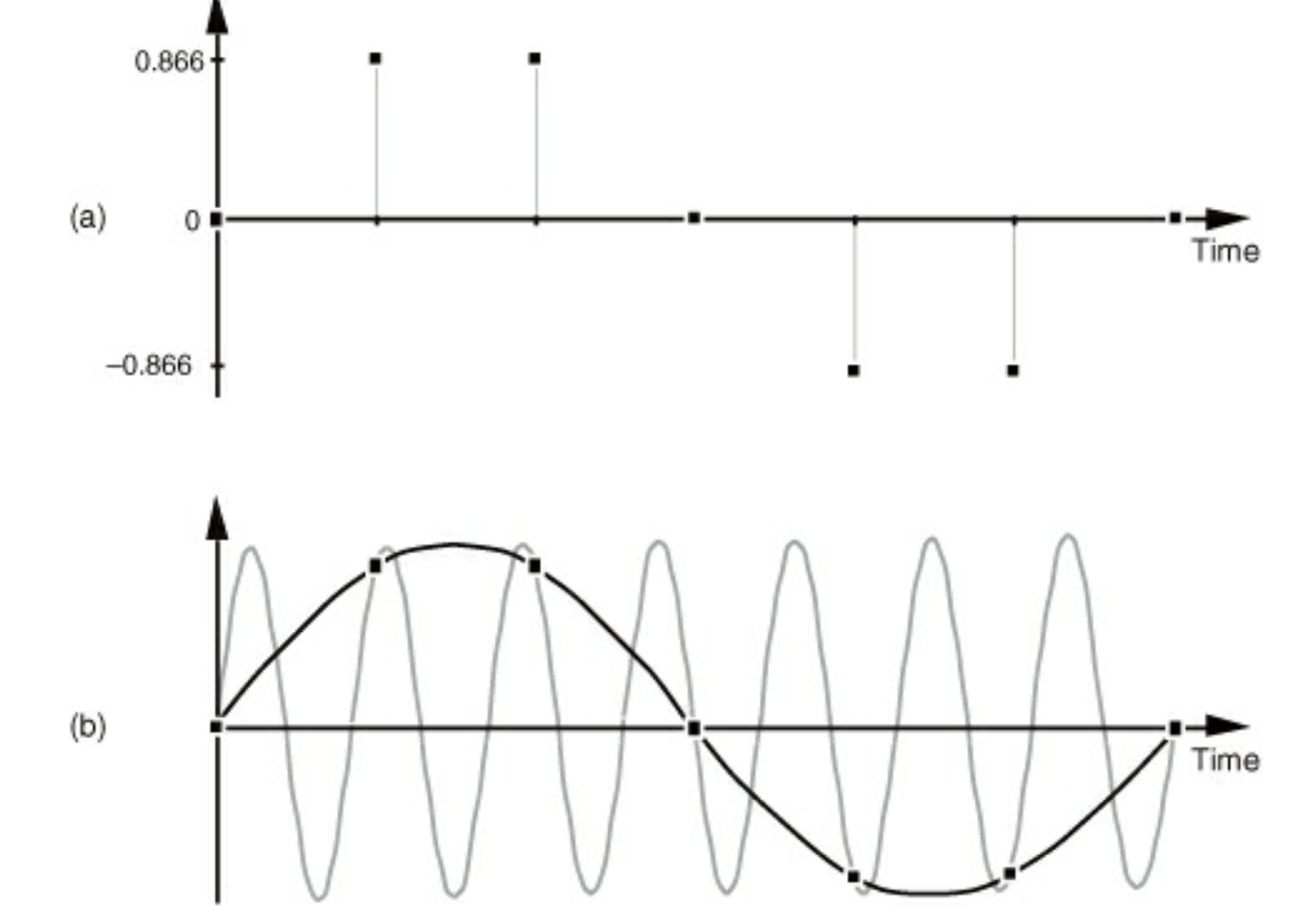
이게 무슨 소리냐면 우리는 원래 신호를 절대 알 수가 없다. 측정은 샘플링을 통해서 하기 때문에 우리가 얻는 값은 원래 신호가 아니고 샘플링 신호다.

그래서 샘플링 값을 1000hz로 측정했을 때 원래 신호가 300hz인지 1300hz인지 2300hz인지 구별하지 못한다는 것이다. 위 그림을 보면 샘플링으로 측정된 값이 점의 값인데 이걸 추측해서 원래 신호를 추정하는 것이다. 근데 아래 그림을 보면 2가지 파동의 경우 모두 가능하단 것을 알 수 있다.

하고 싶은 말은

길게도 써놨는데 결국 하고 싶은 말은 우리 주파수의 기준은 샘플링 주파수란 것이다. DFT가 원래 신호 주파수가 아닌 샘플링 주파수를 기준으로 하는 것은 당연한 일이다. 원래 신호 주파수를 절대 모르기때문

DFT의 간략한 의미

그럼 샘플링 주파수 fs를 기준으로 한다는 것을 확인했으니 우선 exp(x)에 대해서 알아보자.

DFT는 익스포넨셜 함수를 이용하는 데 오일러 공식을 활용해보자.

일단은 뇌 빼고 한 번 보자. 복소수 함수의 크기를 측정하는건 내적으로 한다. 내적은 켤레복소수를 곱해서 적분하면 되는데 켤레 복소수를 곱하면 어떻게 될까?

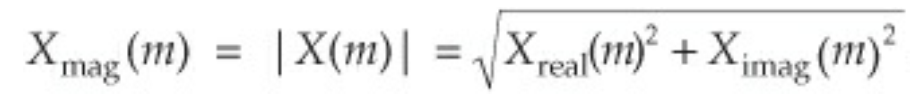
실수 부분과 허수 부분은 서로 독립이다. 독립이니까 서로 직교한다고 생각하면 된다.

그래서 켤레를 곱하면 위와 같이 표현되는 데 이거 완전 피타고라스 삼각형 아니냐?

실수와 허수 부분이 직교한다고 했으니 x, y 좌표처럼 생각하고 크기는 피타고라스 공식이라 직각 삼각형이고 주기 함수라 2파이 마다 반복되네?

이거 완전 원의 정의랑 똑같은 거 아님? 그래서 원으로 많이 표현한다.

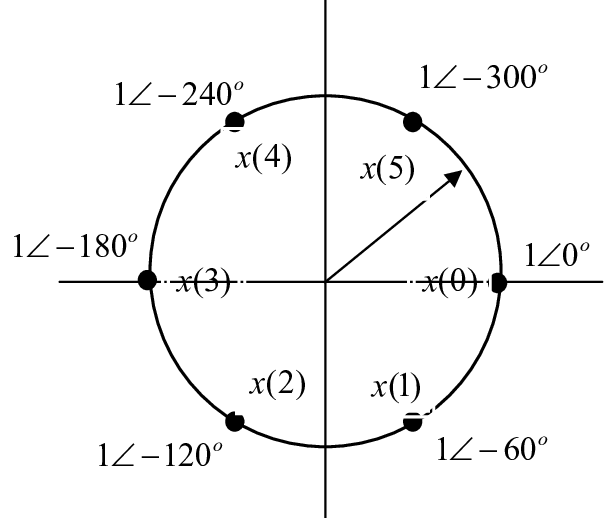
DFT는 샘플링 주파수(fs)에서 일정한 간격으로 데이터 선택하는 것이다.

아까 원처럼 생각할 수 있다고 했으니 원으로 보면 저기 그림에서 점인 부분만 얻는다는 소리다.

만약에 내가 데이터를 많이 얻겠다면 점들이 많이 찍혀서 결국엔 원처럼 보이겠지?

아무튼 중요한 점을 집고 넘어가자. DFT는 입력신호에 적용된다.

중요한 가정을 하고 넘어가겠다. 샘플링에서 선택한 점들이 주기적으로 보인다는 점

뒤에 설명하겠지만 이게 leakage의 발생조건을 정한다.

fs = 8000hz라고 해보자. 그리고 8개의 점을 선택할거다.
m * fs / N 을 선택할거니까. 0KHz, 1000Hz, 2000Hz, 3000, ..., 7Khz

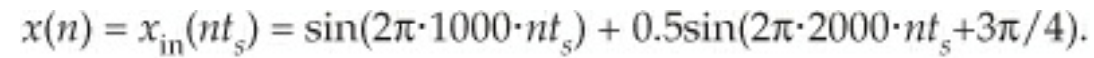
입력 신호는 위와 같다고 하자.

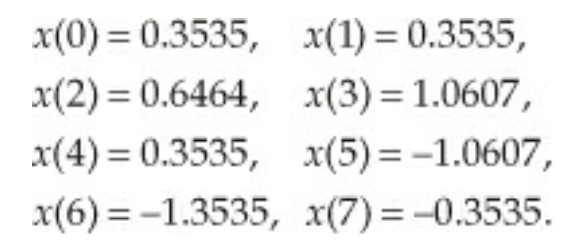
그럼 8개의 점에 대해서 신호의 세기는 위와 같다. 이걸 이용해서 DFT를 구하겠다.

DFT의 1kHz의 크기를 구해보자.

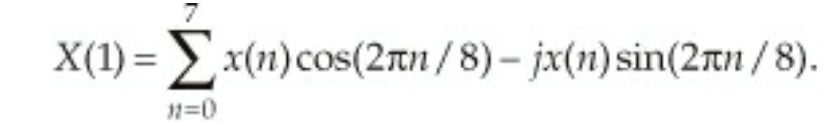
식은 위와 같다. 펼처보면

위 전개식을 보면 값들이 상쇄되고 하나의 위상에 대해서만 값이 나오는걸 알 수 있다.

DFT의 2kHz의 크기를 보자.

역시나 하나의 위상에 대한 값만 나오고 나머지는 상쇄되는 걸 알 수 있다.
잠깐 여기서 위상은?

이 그림 다시보면 우리가 DFT의 exp(x)함수에 대해서 원으로 나타내고 각각의 점들을 주파수로 나타냈다. 여기서 위상이란 DFT의 특정 주파수 값을 의미한다.

위 예제에선 저 원에 8개의 점이 찍혀있고 각각의 고유한 각에 대해서 1kHz, 2Khz, ... 이런식이라고 생각하면 된다.

결론은 DFT에서 내가 선택한 주파수에 맞는 위상값이 하나만 남고 나머지 주파수의 값들은 상쇄되어 없어진다는 뜻이다.

정확하게 설명해줌

상쇄된다는 게 정확히 어떤 의미이고 어떤 조건이 있냐?

조건 - 입력 신호

입력 신호를 샘플링 해서 N개를 선택했을 때 정확히 주기적이여야 한다.

무슨 말이냐면

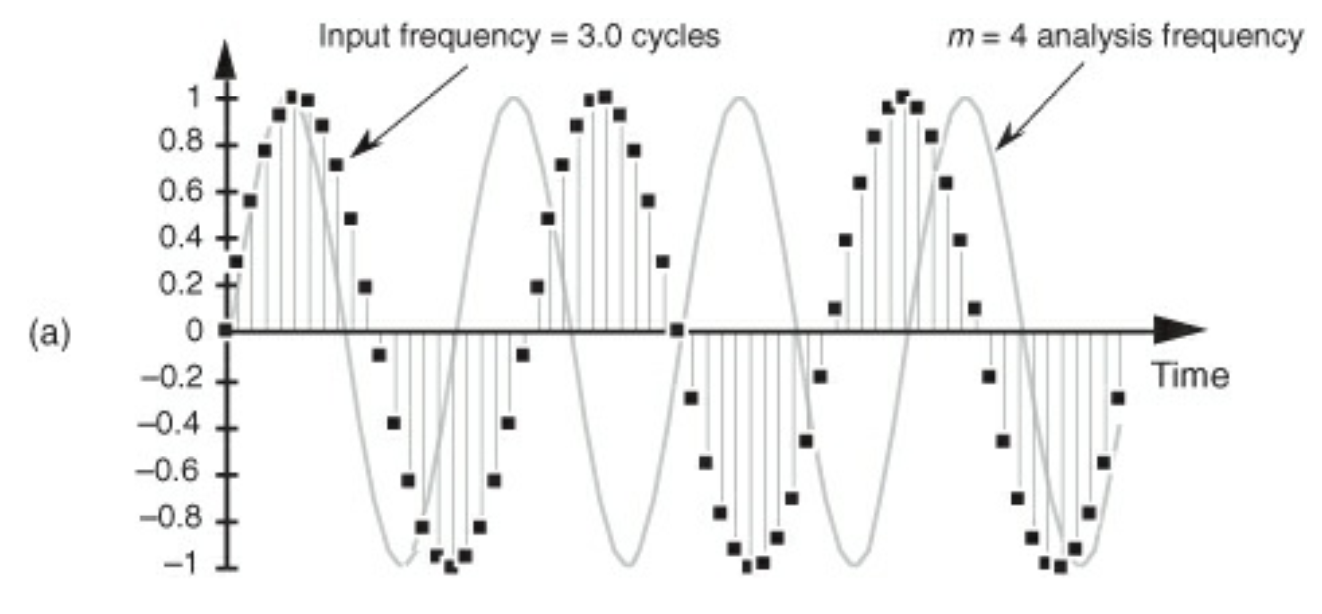
위 그림의 점들이 샘플링한 입력신호들인데 정확히 주기적인것을 알 수 있다. 일단 주파수 0초에선 값이 0이라 제외하고 생각해보면 3주기로 반복적인것을 알 수 있다.

입력 신호가 정확히 주기적이여야 주파수들이 상쇄되어서 하나의 위상값만 남는다.

식으로 보자.

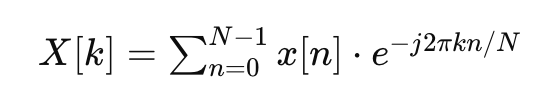
위 식에서 x[n]은 다음과 같다.

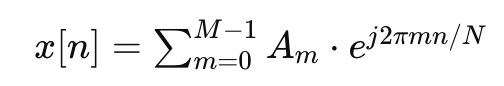
이제 x[n]을 위 식에 대입해보자.

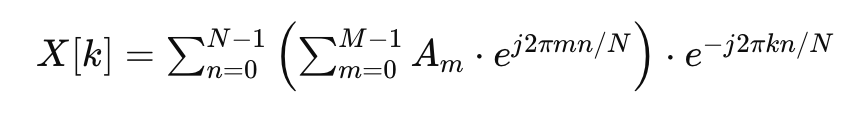
식을 정리하자.

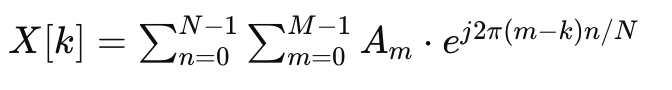
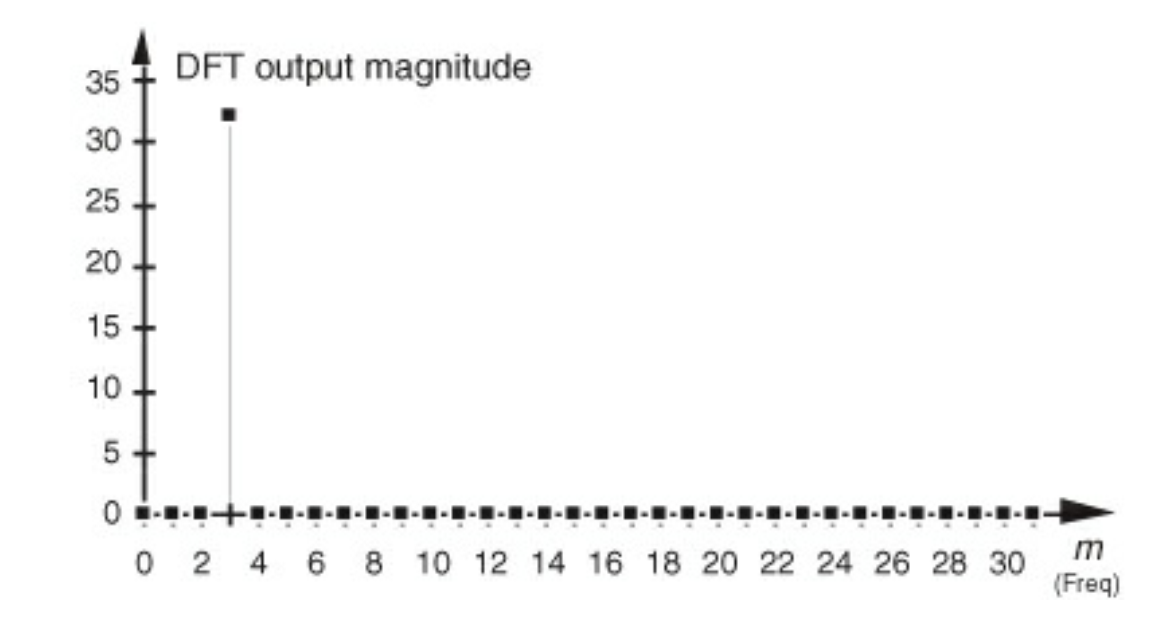
그림을 보면 m = 3에 대해서 즉 X(3)은 3Khz의 값만 정확하게 하나 구해지는 것을 볼 수 있다.

입력신호가 주기적이면 Am또한 주기적으로 같은 값이다.

그럼 위 식을 전개해보면 완벽하게 상쇄가 되고 m = k 의 값에서만 남는다는 것을 알 수 있다.

정말 중요한건 입력 신호가 완벽히 주기적이여야 Am의 값이 같아서 상쇄가 된다는 것.

비주기적인 입력신호는 leakage를 만든다.

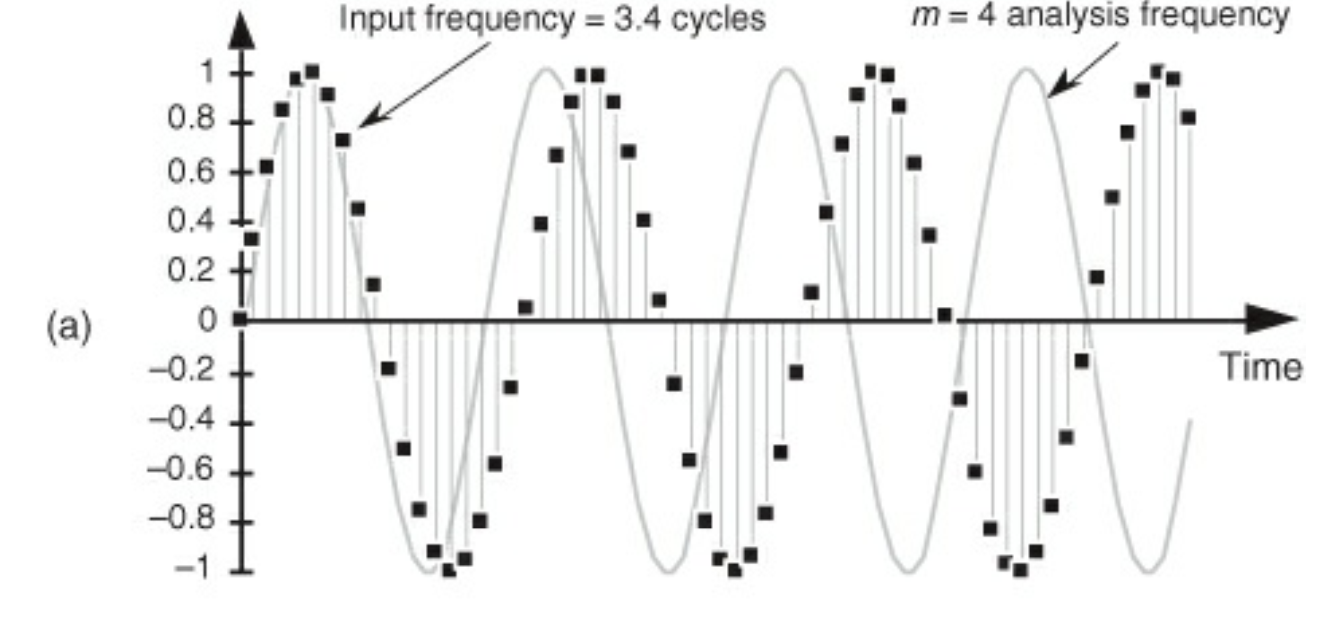
위 그림과 같이 샘플링 값들이 주기적이지 않다고 생각해보자.

그렇다면 DFT의 값에서 Am값들도 대칭이 아니고 식들이 완벽하게 상쇄되지 않겠지?

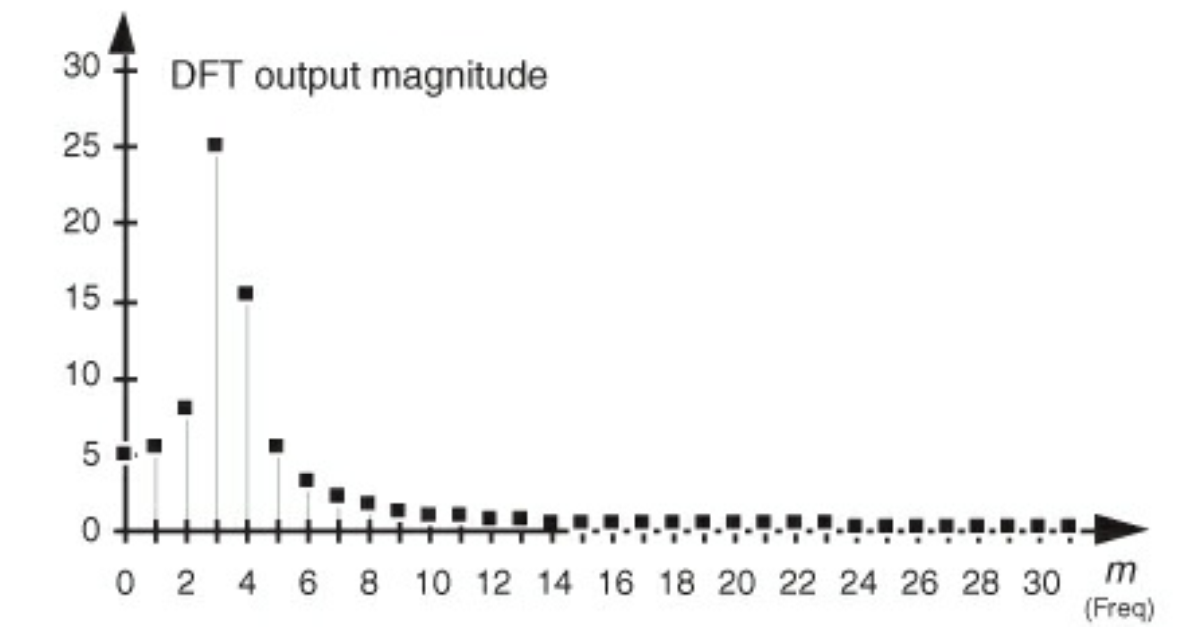
실제로 보자 내가 원하는 값은 특정한 하나의 주파수에 대해서 값이 하나만 있어야 하는 데? 위 그림은 여러 주파수가 값들을 가지고 있다.

DFT의 의도는 하나의 위상 값들이 대응되는 것 인데 위 처럼 상쇄가 되지 않아서 주변 주파수 위상값들이 살아있는 볼 수 있다.

이처럼 의도하지 않은 주파수가 살아있는게 spectral leakage라고 한다.

이유는 Am의 값, 즉 위 신호의 값들이 대칭적이지 않아서 상쇄가 불가능 하기 때문이다.

결론

Spectral leakage의 원인은 입력 신호가 완벽히 주기적이지 않아서 값이 상쇄되지 않기 때문에 생성되는 것이다.

윈도우 함수가 어떤 영향을 줄 수 있겠지만 Spectral leakage의 본질적인 원인은 아니다.

본질은 완벽히 주기적인 입력신호가 아니여서 일어나는 현상이다.

그렇다면?

입력신호가 완벽히 주기적인게 어떻게 일상생활에서 존재하겠나. 우리가 표현하는 사인형태의 신호는 정말 이상적인 신호고 일상 생활에서 얻는 신호는 무조건 비주기적인 이상한 형태의 신호다.

특히 우리가 관심있는 음원 신호인 wav파일만 봐도 비주기적인 신호란 것을 알 수 있다.

즉 우리가 다루는 음원 데이터를 가공할 때 fourier-transform이 사용되는 데 우린 절대 spectral leakage를 피할 수 없다는 점.

그 spectral leakage를 줄이기 위해 사용하는 게 윈도우 함수이다.

음악 딥러닝에 익숙해졌다면 더 좋은 데이터의 품질을 위해 윈도우 함수를 선택해 spectral leakage를 줄이는 걸 고려해야 한다.