물리 에너지 공식

음파의 경우도 줄에서 유도한 에너지 공식을 쓸 수 있다. 왜냐하면 본질적으로 주기운동인점이 같아서. 대충 그림으로 볼려고 했는데 그림 찾기 귀찮아서 말로 설명함

줄의 파동을 보면 줄이 제자리에서 이동하는 것과 옆으로 이동하는 환장의 콜라보인걸 알수 있지.

물리에서 에너지는 1/2 곱하기 질량 곱하기 속도의 제곱이다. 줄의 전체 질량을 따지기는 애매하다. 그럴때 물리가 하는 짓은 존나 나눠서 다시 적분으로 조립하는 거다.

줄을 존나 나눠서 생각하자. 줄의 존나 나눈 질량 즉 단위 질량을 dm라고 하자.
줄의 단위 질량 어떻게 구하냐? 우리가 아는건 줄의 밀도를 알 수 있다고 치고 밀도에 길이를 곱하면 질량이다. 그냥 그렇게 알도록

dm = u * dx

그럼 줄이 위아래로 움직이지? 그럼 속도는 뭐겠어? y축으로 왔다갔다하는 속도겠지뭐

dv = ay / at

그럼 운동에너지는 1/2 곱하기 dm 곱하기 (ay / at) ^ 2
그리고 퍼텐셜 에너지는 그냥 용수철이라고 생각해서 구하면 1 / 2 곱하기 k 곱하기 y^2 이다.

여기서 파동의 방정식을 y = A * sin(kx - wt)에서 영감을 얻자. 정말 귀찮은 작업이고 물리학에 관심 있는거 아니니까 결론만 적겠다.

위에서 구한 퍼텐셜과 운동에너지에 파동 방정식을 도입해서 계산해주면

파동의 에너지는 (1 / 2) 곱하기 u 곱하기 (A ^ 2) 곱하기 w ^ 2 곱하기 dx이다.

헛소리가 길었는데 결론은 음파의 에너지는 A ^ 2, 즉 음파의 세기인 음압의 제곱에 비례한다는 걸 말하고 싶었다. 근데 그냥 그렇다고 하면 왜 그럴까 생각하는 사람을 위해 개소리좀 적어봄.

Root-mean-squared energy

그럼 내가 왜 개소리를 저렇게 많이 썼을까? 당연히 Root-mean-squared energy 때문이지. Root-mean-squared energy의 공식을 살펴보자.

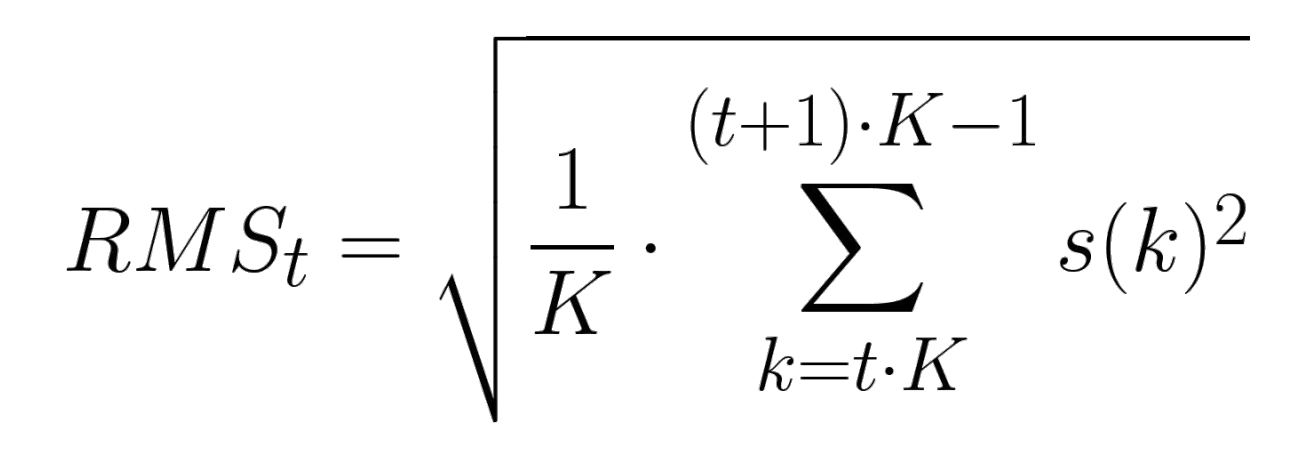
이 공식은 지금 연재하고 있는 이 시리즈를 뒤적이면 설명이 있어요

자 공식을 봐라 s(k)가 에너지야. 정말 뜬금없이 에너지가 나오지 이게 왜 에너지를 구하는게 있냐?

그래서 내가 개소리를 많이 적어 논거다. 음파의 에너지와 음파의 세기 즉, 음압은 비례관계에 있어요. 한 쪽을 알면 자연스럽게 추측을 할 수 있다는 소리다.

그럼 이렇게 생각할 수 있다. 그냥 음압을 직접 측정하면 되는거 아님? 음압을 측정하는 기계는 비싸고 만들기도 어렵다. 대신 파동의 에너지를 측정하는 기계는 진짜 흔하고 싸게싸게 할 수 있다.

그럼 가성비 있게 음압보단 에너지를 측정하는 게 좋겠지? 그래서 Root-mean-squared energy이걸 구하는 거다. 에너지로 음압을 알려고

librosa로 Root-mean-squared energy 구현

ipynb 파일을 만들어주자.

import matplotlib.pyplot as plt
import numpy as np
import librosa
import librosa.display
import IPython.display as ipd

저번처럼 필요한 라이브러리를 로딩해주자.

음원 로딩

내 음원이 있는 경로를 가져와서 음원 객체를 생성하자

metallica = "/Users/seong-gyeongjun/Downloads/bugs_20230422165203/72 Seasons_Metallica_72 Seasons.mp3"

""에는 내 파일의 경로를 지정하면 된다.

ipd.Audio(metallica)

해주면 음원이 맞는지 확인 할 수 있다.

librosa로 파일 로딩

metallica, sr = librosa.load(metallica)

저번처럼 librosa.load()를 이용해서 음원을 로딩 해주자.

framesize, hoplength 조절

FRAME_SIZE = 4096
HOP_LENGTH = 2048

librosa는 프레임을 기준으로 전처리를 하니 framesize를 조절 해주자. 나중에 시각화가 맘에 안들면 여길 수정하면 된다.

librosa.feature.rms()

librosa.feature.rms(*, y=None, S=None, frame_length=2048, hop_length=512, center=True, pad_mode='constant', dtype=<class 'numpy.float32'>)

매개변수에서 y는 audio time series로 우리가 구할 값이고
s는 spectrogram 파일을 뜻한다.

rms_metallica = librosa.feature.rms(y=metallica, frame_length=FRAME_SIZE, hop_length=HOP_LENGTH)[0]

이렇게 rms를 구해주자. 만약 직접 공식을 이용해 구하고 싶으면

def rmse(signal, frame_size, hop_length):
    rmse = []
    
    # calculate rmse for each frame
    for i in range(0, len(signal), hop_length): 
        rmse_current_frame = np.sqrt(sum(signal[i:i+frame_size]**2) / frame_size)
        rmse.append(rmse_current_frame)
    return np.array(rmse)   

이렇게 구하면 된다.

frames = range(len(rms_metallica))
t = librosa.frames_to_time(frames, hop_length=HOP_LENGTH)

시간에 대한 그래프를 그려야하니 librosa에서 시간을 구하는 매서드를 이용해준다.

rmse 시각화

plt.figure(figsize=(15, 17))

ax = plt.subplot(3, 1, 1)
librosa.display.waveshow(metallica, alpha=0.5, color="blue")
plt.plot(t, rms_metallica, color="r")
plt.ylim((-2, 2))
plt.title("metallica")

plt를 이용해서 rms를 빨간색으로 librosa.display.waveshow를 이용해서 음원을 그래프로 표현해주자.

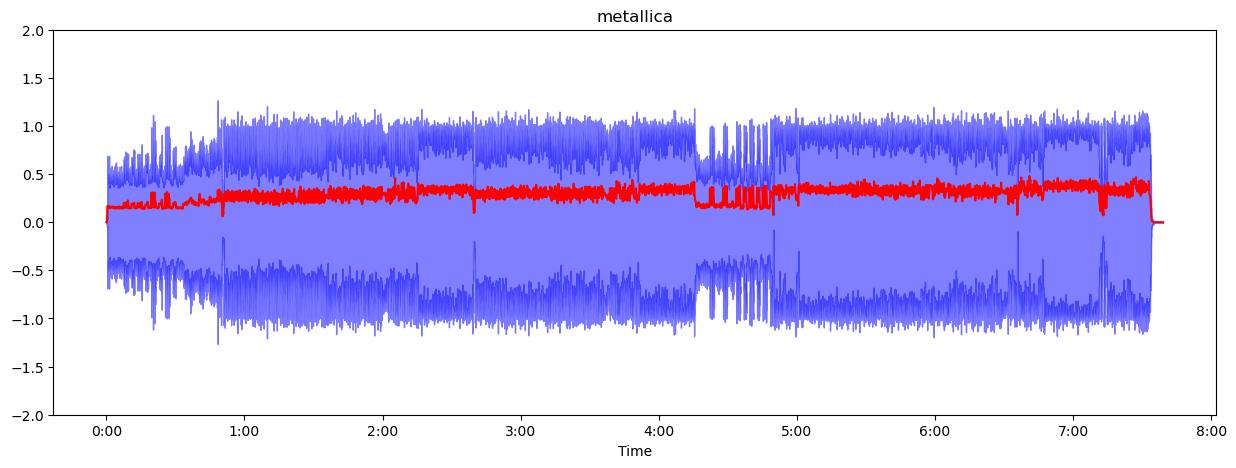
만약 빨간색이 위아래로 길고 뭔가 안 이쁘면 frame size를 늘려주자. 너무 적게 표시되면 frame size를 줄여주면 된다.

Zero-crossing-rate

Zero-crossing-rate는 앞선 시리즈에서 말했듣이 단위 시간당 음압의 부호가 바뀐것을 측정하는 것으로 주파수의 개념과 똑같다. 즉 Zero-crossing-rate는 주파수를 간접적으로 추측하기 위해서 구한다고 생각하자.

librosa로 Zero-crossing-rate 구하기

zcr_metallica = librosa.feature.zero_crossing_rate(metallica, frame_length=FRAME_SIZE, hop_length=HOP_LENGTH)[0]

librosa.feature.zero_crossing_rate()로 구해주자.

librosa.feature.zero_crossing_rate(y, *, frame_length=2048, hop_length=512, center=True, **kwargs)

y는 audio time series이고 **kwargs는 추가하고 싶은 매개변수다. 예를 들어서

zcr = librosa.feature.zero_crossing_rate(y, threshold=0.1)

threshold를 추가할 수 있다.

zcr_metallica.size

개수는 위와 같이 구할 수 있다.

plt.figure(figsize=(15, 10))

plt.plot(t, zcr_metallica, color="y")
plt.ylim(0, 0.6)
plt.show()

plt이용해서 구해주자.

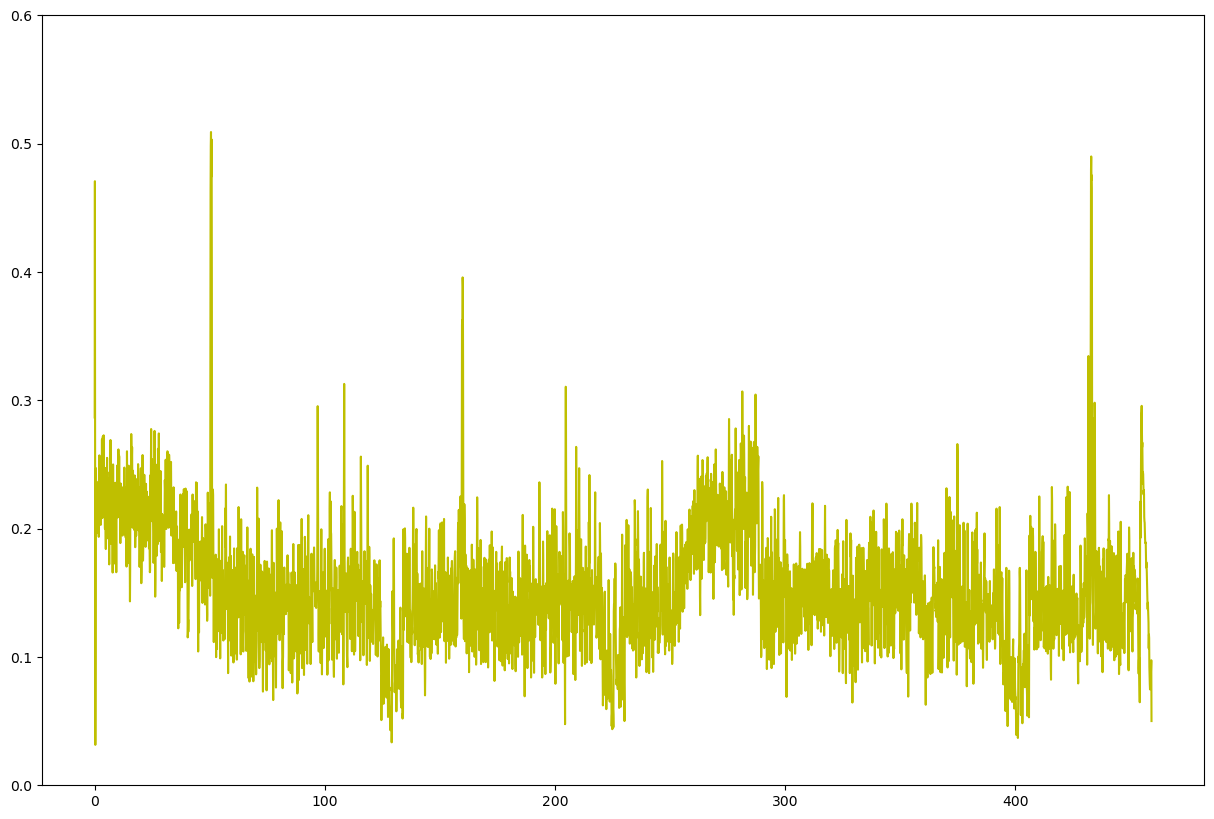
그래프는 위와 같다.