analog signal

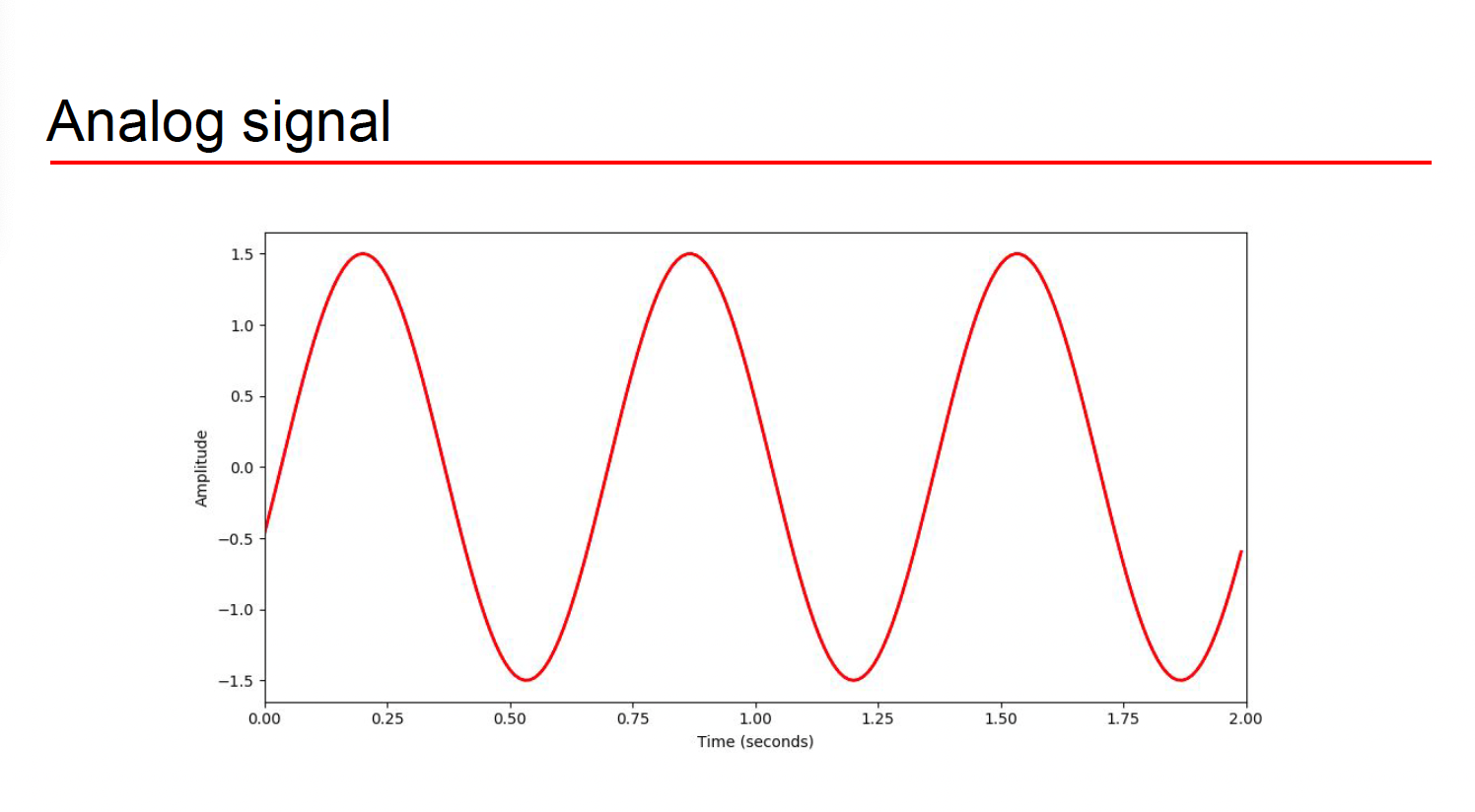
우리가 일상 생활에서 발생하는 신호를 analog signal이라고 한다. 일상의 모든 소리는 파동이 연속적이다. 위 그림을 보라 이상적이고 연속적이고 매끄러운 데이터이다. 이런 일상적인 파동은 연속적이고 미분가능해서 푸리에 변환에 큰 무리가 없다. 근데 문제가 기계의 원리가 연속적이지 않다는 점이다.

이런 연속적인 파동을 데이터로 컴퓨터가 뭘 할 수가 없다. 컴퓨터가 2진법 비트를 이용해서 불연속적으로 데이터를 처리하기 때문에 이 파동도 불연속적으로 나누어서 데이터로 만들어야 컴퓨터가 잘 활용할 수 있다.

Sampling

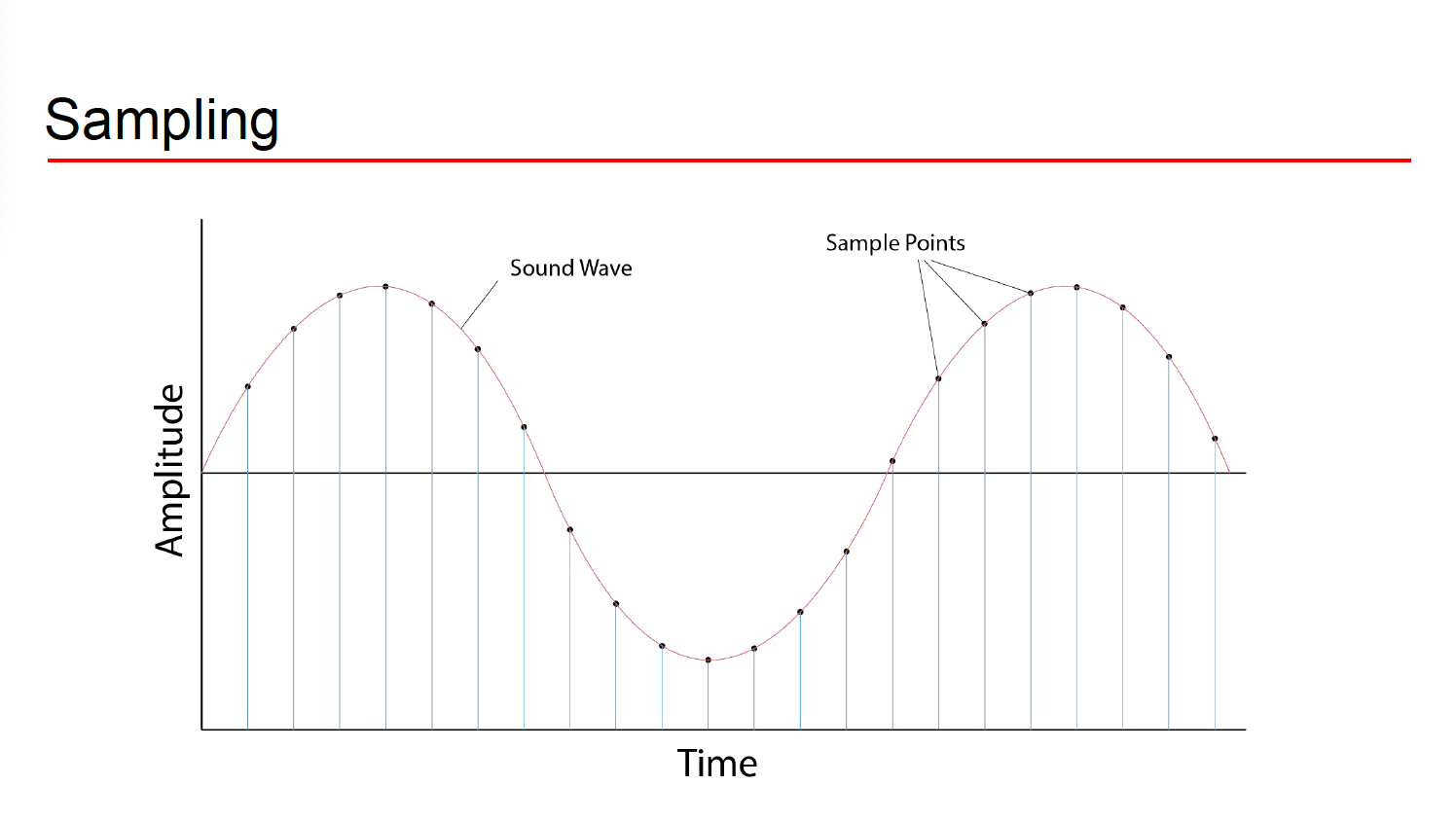
불연속적인 디지털 신호로 바꿀려면 어떻게 할 까? 뭐긴 뭐여 걍 쪼개면 된다.
고등학교 시간에 적분을 배우면 그래프를 네모모양으로 존나 짜르는걸 볼 수 있다. 여기서도 존나 짜를거다. 그걸 샘플링이라고 한다고

적분에서도 x축의 구간을 일정하게 짜르는 것 처럼 소리도 시간 간격을 일정하게 짜를거다. 그래야 수학적으로 접근하기 편하니까.

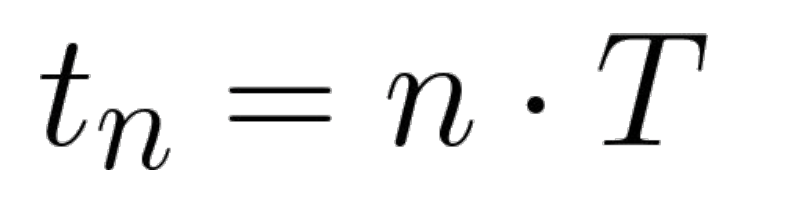
그러면 짜른 신호의 위치를 어떻게 알 까? 뭔 말이냐면 개 많이 쪼개서 현재 조각의 시간이 전체 신호의 어디에 해당하는지 알려면? 간단하게 몇번째 조각인지 확인하고 거기에 시간 간격만 곱해주면 해결된다. 그게 저 위의 식이다.

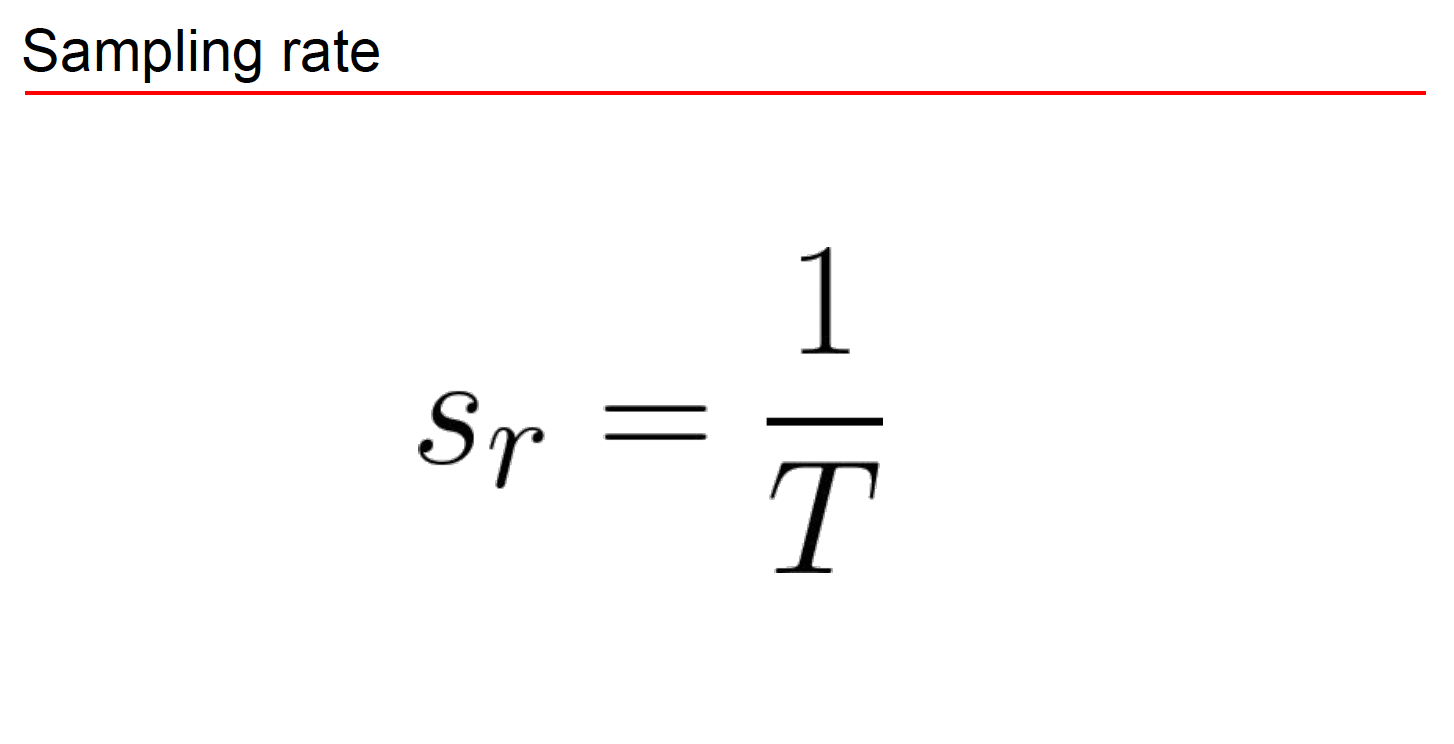
그럼 진동수(주파수)는 어떻게 아냐? 자른 시간 간격의 역수를 해주면 안다. 하나 자르는데 2초 만큼 걸린다고 생각해보자. 그러면 1초에 몇개나 짜르는거여? 그럴때 걍 역수를 취해주면 1/2 개가 나온다는 거지. 주파수는 1초에 몇개나 짜르냐를 따지니까 역수를 취하라고

Aliasing

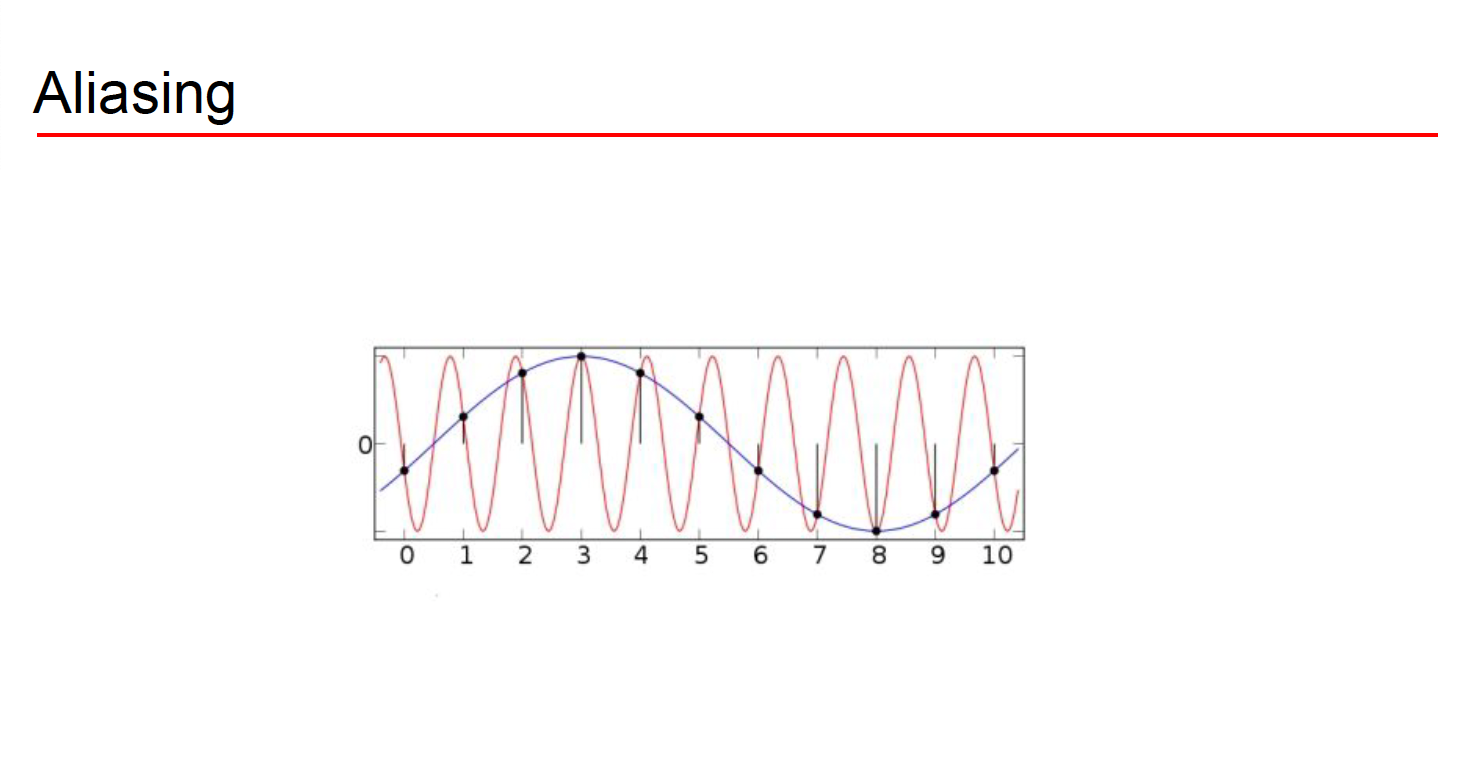
신호를 짜르는데 그럼 어떤 시간 간격으로 짤라야 좋을지 고민이 되기 마련이다.

개 많이 짜르면 좋은거 아님? 응 아님

개 많이 짜르면 컴퓨터의 자원이 많이 들어가서 음원 크기가 너무 커진다. 항상 엔지니어는 가성비를 따져야 한다.

그러면 대충 적게 짜르면 되는거 아님? 응 아님

적게 짜르면 생기는 문제가 저 위의 aliasing이다. 원래 음원을 적게 짤라서 네모 크기가 크다고 생각해봐라.

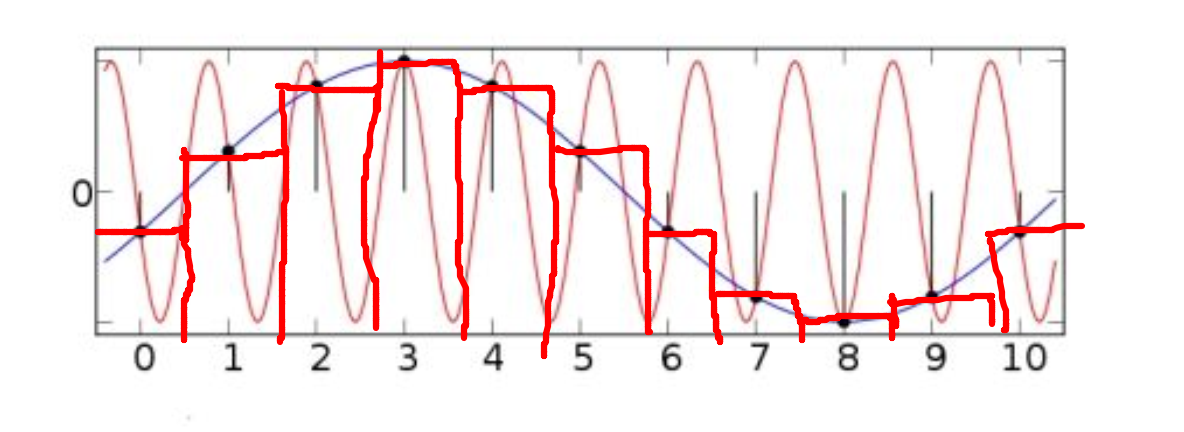
요렇게 자른다고 생각해봐라 그리고 배경에 있는 원래 신호는 잊어 버리고 그러면 신호를 대충 네모의 가운데 값으로 예측해본다면 파란색 그래프처럼 보이겠지? 근데 그건 원래 신호가 아닌 전혀 다른 신호잖아. 그니까 적게 짜르다가 ㅈ 될 수 있다는 말이 aliasing이다.

물론 지금 내용만 설명할려고 저렇게 짤랐는데 그냥 자른거고 실제론 저렇게 안 짜른다.

Quantization

양자적으로 자른다는 게 그냥 디지털로 불연속적으로 자른다는 말이다. 몇 가지 특성을 알아보자.

Resolution = bit depth
해상도란 말인데 내가 자른 하나의 샘플에 담긴 비트의 수를 이야기 한다. 해상도가 16이란 말은 내가 쪼갠 하나의 샘플에 2^16 = 65536개의 비트가 들어있다는 말이다.

음원 1분에 필요한 메모리 양

음원 파일 1분에 메모리 용량이 얼마나 필요한 지 계산해보자.

bit depth = 16bit, sample rate = 44100hz라고 하면

bit depth 곱하기 sample rate 곱하기 60초 곱하기 (mb)로 변환하는 보정 상수

= 16 곱하기 44100 곱하기 60 곱하기 1048576 / 8 mb = 5.49mb이다.

데이터치곤 상당히 큰 양이다.

그래서 가성비있게 메모리를 절약 해주는 테크닉을 적용 해준다. 그건 나중에 알아보렴

출처

https://www.youtube.com/watch?v=daB9naGBVv4&list=PL-wATfeyAMNqIee7cH3q1bh4QJFAaeNv0&index=4