weight, bias 초기화
모델을 본격적으로 학습하는 코드를 만들기 전에 학습에 필요한 weight와 bias를 초기화하는 매서드를 만들자.
일전에 만들어 둔 common_ops란 파일에 만들 것 이다.
import torch
import torch.nn as nn
def lstm(x, prev_c, prev_h, w):
ifog = torch.matmul(torch.cat([x, prev_h], dim=1), w)
i, f, o, g = torch.split(ifog, ifog.size(1) // 4, dim=1)
i = torch.sigmoid(i)
f = torch.sigmoid(f)
o = torch.sigmoid(o)
g = torch.tanh(g)
next_c = i * g + f * prev_c
next_h = o * torch.tanh(next_c)
return next_c, next_h
def stack_lstm(x, prev_c, prev_h, w):
next_c, next_h = [], []
for layer_id, (_c, _h, _w) in enumerate(zip(prev_c, prev_h, w)):
inputs = x if layer_id == 0 else next_h[-1]
curr_c, curr_h = lstm(inputs, _c, _h, _w)
next_c.append(curr_c)
next_h.append(curr_h)
return next_c, next_h
def create_weight(name, shape, initializer=None, requires_grad=True):
if initializer is None:
initializer = nn.init.kaiming_normal_
weight = torch.empty(*shape)
initializer(weight, mode='fan_in', nonlinearity='relu')
return nn.Parameter(weight, requires_grad=requires_grad)
def create_bias(shape, initializer=None):
if initializer is None:
initializer = nn.init.constant_
bias = torch.empty(*shape)
initializer(bias, 0.0)
return nn.Parameter(bias)초기화를 잘하자
가중치를 초기화하는 과정은 머신러닝의 학습에서 중요한 역할을 한다. 실제 학습해보면 알겠지만 가중치를 잘못 초기화 할 경우 처음 학습 epoch의 속도가 정말 느리다. 가중치를 잘못 초기화하면 학습의 대부분을 처음 epoch를 학습하는데 쓸 것이며 대용량 데이터의 경우 많은 리소스를 써야되는 부담이 생긴다.
또한 학습에는 기울기 소실과 기울기 발산 문제가 항상 존재하는 데 이러한 문제를 해결하기 위해 초기화하는 범위(분산과 평균)를 신경써야한다.
분산에 대해서 이야기 해보기 전에 논문에서 언급되는 간단한 사실부터 명시하고 가자
두 독립 변수 A와 𝐵의 곱의 분산은 아래와 같다
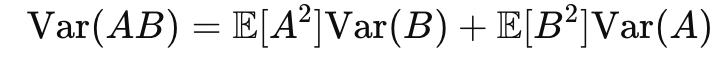
A, B가 여기서 평균이 0이고 서로 독립이라면
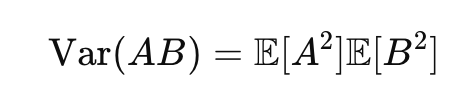
그리고 여러 독립된 랜덤 변수의 합의 분산은 각 랜덤 변수의 분산의 합으로 주어진다.
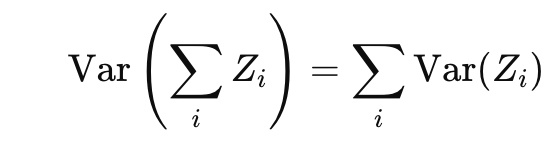
또한 두 변수가 동일한 분포를 따르고 있다고 가정하면 모든 항의 분산은 동일하다
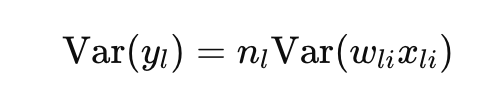
위와 같은 사실을 알고 학습에서 분산에 대해서 생각해보자
전파와 점화식
층이 깊다면 순전파던 역전파던 일종의 점화식으로 생각할 수 있다
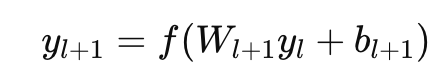
output도 위와 같이 점화식으로 생각할 수 있고
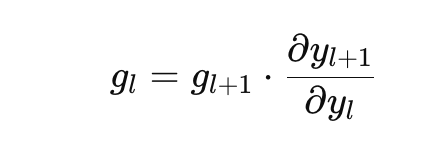
기울기도 위와 같이 점화식으로 생각할 수 있다
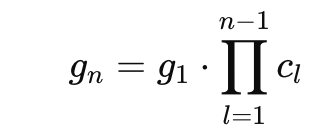
변화률을 c라고 두면 결국 g의 식은 위와 같은 역전파 수식이 되는데
위 식을 자세히 생각해보자.
결국 기울기 소실이나 폭발에 대한 문제는 c가 어떤 값인지 중요한게 아닌가?
더 정확하게 생각해보면 c의 평균과 분포가 안정적인 값들을 가져야지 학습이 잘 되지 c의 값들이 대부분 무척 크다면 기울기 폭발, 무척 작다면 기울기 소실이 일어난다
이걸 예방하기 위해서 선택하는게 c의 평균을 0으로 분산을 1로 둬서 극단적인 기울기를 방지하자는게 기본 아이디어다
당연히 유명한 정규분포가 쓰였지만 레이어가 깊어질 수록 다양한 문제가 생겨 나온게 xavier 초기화다
xavier 초기화
초기화의 핵심 아이디어에서 말했듣 입력값과 출력값이 극단적이지 않고 적절하게 선택되야 한다
그럼 xavier 초기화의 핵심 아이디어는 뭘까?
xavier 초기화의 핵심 아이디어는 분산의 합을 고려하여 입력과 출력의 분산이 층을 거쳐 전파될 때 너무 커지거나 작아지지 않도록 보정하는 것이다
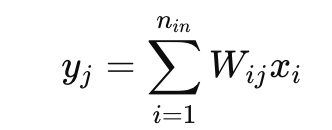
에서 y의 분산은 앞서 말했듣 W, x의 합들로 이루어져 있어서
n개의 독립적인 항들이 더해지기 때문에 분산이 증가할 수 있다.
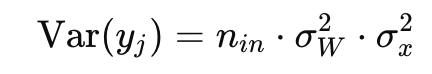
역전파 역시 nout의 개수만큼 분산이 넓어지게 되는데 이걸 평균 0, 분산인 1로 만들어주기 위해서 w의 분산을 보정해주자가 xavier의 내용이다
수식 전개는 다음과 같다
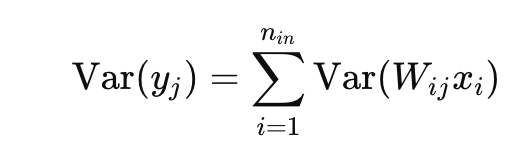
에서 w, x는 독립이기 때문에
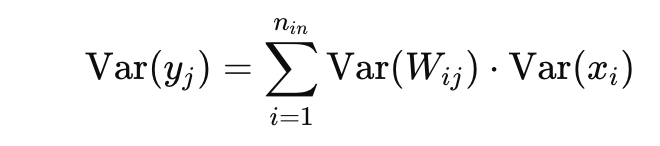
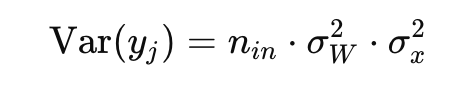
로 두면
분산의 점화식이 극단적으로 변하지 않기 위해선 1이 점화되면 된다. 이 말은 입력의 분산과 출력의 분산이 같으면 된다는 말이다. 점화식이란 입력데이터에 w가 계속 곱해져서 점화되니 w의 분산을 조정하자. 분산이 1로 점화되면 입력값과 출력값의 분산이 같다는 말이니 아래와 같은 식이 된다.
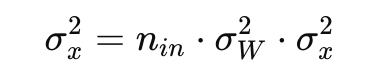
이 식이
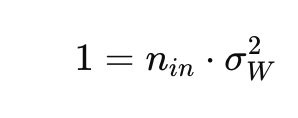
로 점화식이 1이 되게 위와 같이 두면
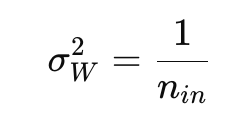
이런 식으로 순전파에선 입력의 개수를 보정, 역전파에선 출력의 개수를 보정해준다.
He 초기화
위에서 xavier 초기화를 살펴 보았다면 이번엔 He 초기화를 한 번 보자.
He 초기화는 Relu activation을 적용했을 때 분산을 안정적으로 만드는 기법이다
w가 평균이 0인 대칭적인 분포를 가정하고 b = 0으로 생각하자
y(l-1)은 가중치 w(l-1)이 대칭적인 분포를 가지고 있기 때문에 y(l-1) 역시 대칭으로 평균이 0이다
Relu 함수는 f(x)=max(0,x)와 같이 표현되며 음수인 값들을 0으로 만든다
Relu를 통과한 y(l-1)의 출력값인 x(l)은 음수인 부분이 0이 되므로 더 이상 대칭이 아니다.
절반의 값이 0이 되므로 분산 또한 절반이 된다.
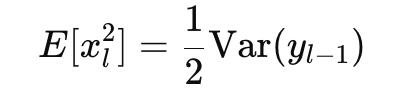
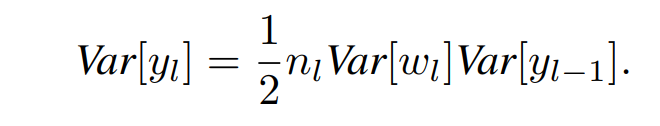
따라서 우리가 위에 xavier에서 전개한 식에서 Relu는 1/2만 곱해주면 된다
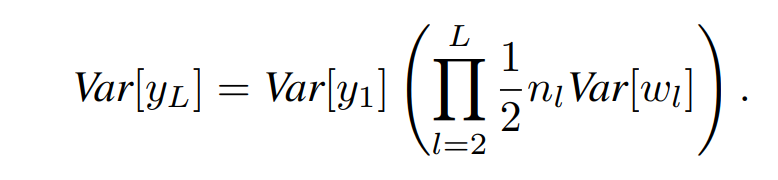
따라서 분산의 점화식또한 위와 같이 표현가능하다
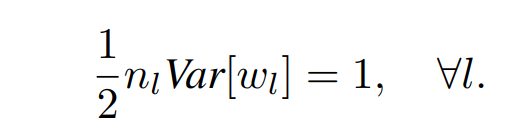
xavier와 같이 우리가 기울기 문제를 안전하게 만들기 위해서 점화식에 적용되는 곱을 1로 만들면 되니 위와 같은 조건을 두면 된다
따라서 He 초기화는 가중치(w)의 분산을 안정되게 2/n으로 만드는게 핵심이다
