Regularization

정규화

딥러닝을 진행하다보면 자주 나오는 용어이다. 영어로 Normalization, Standardization, Regularization 이 세 용어는 한국어로는 모두 정규화지만 각각 다르기 때문에 헷갈리기 아주 좋다.

각각의 차이에 대해서 간략하게 살펴보자

Regularization

이 방법은 모델에 제약을 거는 작업으로 이는 모델의 training_accuracy를 낮춰 testing_accuracy를 높이는 것이다. 즉, 모델을 flexible하게 만들어 주는 것이다

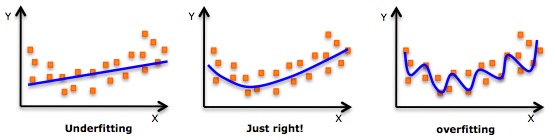
위 그림의 overfitting은 모델이 훈련 데이터에 너무 딱 맞게 학습되었고 이를 가지고 테스트를 진행하면 좋은 결과가 나오지 않을 것이라는 것을 알 수 있다.

이러한 overfitting을 방지해 주기 위해 사용하는 방법이 Regularization이라고 한다.

대표적인 방법으로 dropout, early stopping weight decay 등이 있다.

Normalization, Standardization

이 두 방법은 모두 데이터의 범위(scale)를 compact하게 만들기 위해서 사용한다. 즉, 데이터를 축소하는 re-scaling 한다.

데이터 범위를 축소하는 이유는

• scale의 범위가 너무 크면 노이즈 데이터가 생성될 가능성이 크고 overfitting 될 가능성이 높다
• 값의 범위가 커지면 Activation Function(활성화 함수)의 의미가 희미해진다. 값이 너무 커지면 활성화 함수를 거쳐도 한 쪽으로 값이 치중될 가능성이 높기 때문에
• 일반적으로 Weight 초기화를 위해 정규분포(N(0,1))로 부터 값을 생성하게 된다. 정규분포 값은 $\pm2.58$ 안에 99%가 존재한다. 따라서 scale이 너무 커서 값의 분포 범위가 넓ㅇ면 값을 정하기 힘들어진다.

Scale 조절 방식에 차이가 존재한다.

• Normalization : 이미지에서 픽셀값(0~255)를 255로 나눠 (0~1) 범위의 값으로 축소시키는 방식
• Standardization : 표준화 확률을 구하는 방법. Z-Score 구하기 $\frac{x - \mu}{\sigma}$

Regularization의 종류

L1, L2 Regularization, Dropout, Early Stopping 등이 있다고 했다.
여기서 L1, L2 Regularization에 대해서 알아보자
L1, L2의 숫자는 차수를 의미한다.

L1 Regularization

L1 Regularization을 식으로 표현하면 아래와 같다
$Cost = \displaystyle\sum_{i=0}^{N}(y_i - \displaystyle\sum_{j=0}^{M}x_{ij}W_j)^2 + \lambda\displaystyle\sum_{j=0}^{M}|W_j|$
$Cost = \frac{1}{n} \displaystyle\sum_{i=1}^{n}\{L(y_i, \hat{y_i}) + \frac{2}{\lambda}|W|\}$

• 기존의 Cost Function에 가중치의 절대값을 더한 값이다.
• 기존의 Cost Function에 가중치가 포함되면서 가중치가 너무 크지 않은 방향으로 학습되도록 한다.
• $\lambda$가 0에 가까울 수록 정규화의 효과는 없어진다.
• L1 Regularization을 사용하는 Regression model을 Lasso Regression이라고 한다.

L2 Regularization

L2 Regularization을 식으로 표현하면 아래와 같다
$Cost = \displaystyle\sum_{i=0}^{N}(y_i - \displaystyle\sum_{j=0}^{M}x_{ij}W_j)^2 + \lambda\displaystyle\sum_{j=0}^{M}{W_j}^2$
$Cost = \frac{1}{n} \displaystyle\sum_{i=1}^{n}\{L(y_i, \hat{y_i}) + \frac{2}{\lambda}|W|^2\}$

• 기존의 cost function에 가중치의 제곱을 더한다
• L1과 마찬가지로 가중치가 너무 크지 않은 방향으로 학습하도록 도와준다
• Weight decay라고도 한다.
• L2 regularization을 사용하는 Regression model을 Ridge Regression이라 한다

L1, L2 Regularization은 조금더 공부를 해야할 필요가 있다.

Norm

일반적으로 Regularization에 앞서 이해해야 하는 것이 Norm이다.
Norm은 선형대수학에서 가장 유용하게 사용되는 연산자 중에 하나이다. 벡터가 얼마나 큰지를 알려주는 것이 Norm으로, 벡터의 길이 혹은 크기를 측정하는 방법이다. Norm이 측정한 벡터의 크기는 원점에서 벡터 좌표까지의 거리이다

기본 식
$L_p = (\displaystyle\sum_{i}^{n}|x_i|^p)^\frac{1}{p}$

• p는 Norm의 차수를 의미한다. p=1이면 L1 Norm, p=2이면 L2 Norm
• n은 대상 벡터의 요소 수
• Norm은 각 요소별로 요소 절대값을 p번 곱한 값의 합을 p제곱근한 값이다

주로 사용되는 Norm은 L1 Norm과 L2 Norm, Maximum Norm이다.

L1 Norm

p가 1인 Norm으로 Manhattan Norm이라고도 한다.

공식은 아래와 같다.
$L_1 = (\displaystyle\sum_{i}^{n}|x_i|) = |x_1| + |x_2| + |x_3| + \dots + |x_n|$

L1 Norm은 벡터의 요소에 대한 절대값의 합으로 요소의 값 변화를 정확하게 파악할 수 있다.

벡터 x의 L1 Norm 계산
$x = [1,2,3,4,5]$
$||x||_1 = (|1| + |2| + |3| + |4| + |5|) = 15$

L1 Norm은 L1 Regularization, Computer Vision에서 주로 사용된다

L2 Norm

p가 2인 Norm으로 L2 Norm은 n차원 좌표평면에서 벡터 크기를 계산하기 때문에 Euclidean Norm이라고도 한다.

공식은 아래와 같다
$L_2 = \sqrt{\displaystyle\sum_{i}^{n} x_i^2} = \sqrt{x_1^2 + x_2^2 + x_3^2 + \dots + x_n^2}$

아래 공식으로도 표현할 수 있다.
$L_2 = \sqrt{\displaystyle\sum_{i}^{n} x_i^2}$
$= \sqrt{x \cdot x} = \sqrt{x^Tx}$
$= \sqrt{x_1*x_1 + x_2*x_2 + x_3*x_3 + \dots + x_n*x_n}$

벡터 x의 L2 Norm 계산
$x = [1,2,3,4,5]$
$||x||_2 = \sqrt{(|1|^2 + |2|^2 + |3|^2 + |4|^2 + |5|^2)} = \sqrt{1+4+9+16+25} = \sqrt{55} = 7.4161$

L2 Norm은 L2 Regularization, kNN 알고리즘, kmean 알고리즘에서 주로 사용된다.

Maximum Norm

Maximum Norm은 p값을 무한대로 보냈을 때의 Norm, 벡터 성분의 최대값 구한다.

공식은 아래와 같다
$L_\infty = max(|x_1|, |x_2|, |x_3|, \dots, |x_n|)$

좌표 공간에서 L1, L2 Norm 시각화

L1 Norm

$B = [\beta_0, \beta_1]$ 벡터가 있을 때, B 벡터의 L1 Norm이 1이라면 아래와 같이 표현할 수 있다.

$||B||_1 = 1 = |\beta_0| + |\beta_1|$

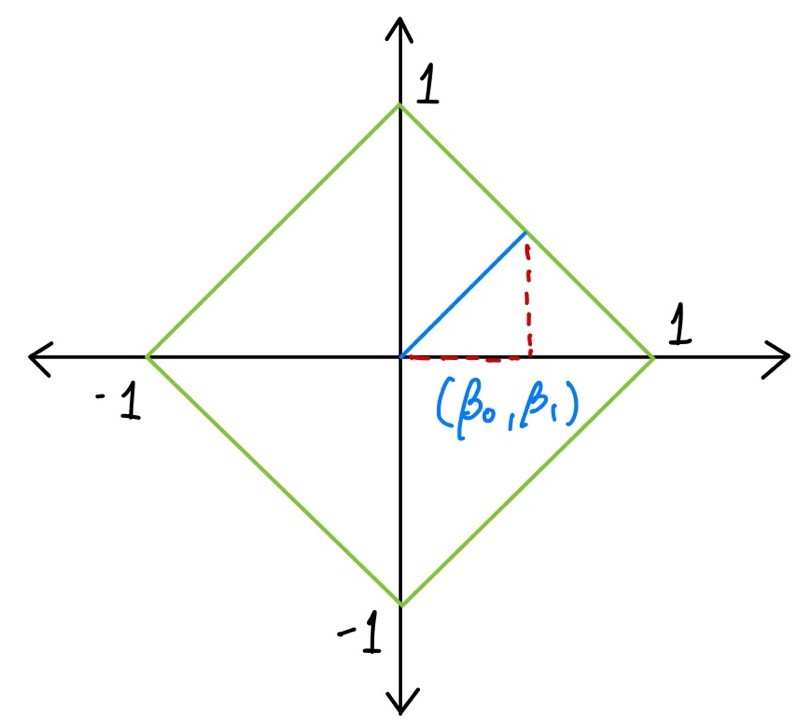
L1 Norm이 가능한 벡터 B는 위 그림과 같이 표현할 수 있다. 벡터 B는 빨간색 마름모 선 위에 위치하게 된다. 마름모 선 = $|\beta_0| + |\beta_1| == 1$인 벡터의 모음이다.

L2 Norm

위 L1 Norm과 같이 $B = [\beta_0, \beta_1]$ 벡터가 있을 때, B 벡터의 L2 Norm이 1이라면 아래와 같이 표현할 수 있다.

$||B||_2 = 1 = \sqrt{\beta_0^2 + \beta_1^2}$

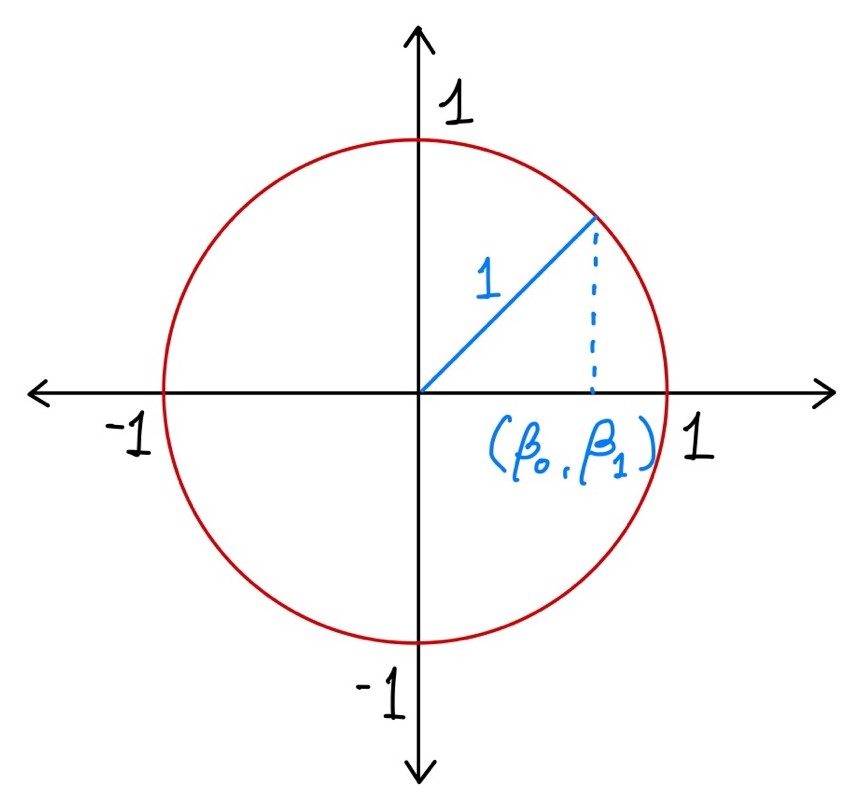
L2 Norm이 가능한 벡터 B는 위 그림과 같이 표현할 수 있다. 벡터 B는 빨간색 원 위에 위치하게 된다 이러한 원을 Unit Circle이라고 한다.

Norm 관련해서 TAEWAN.KIM 블로그 - 딥러닝을 위한 Norm, 노름 블로그를 참고했습니다.

Dropout

Dropout은 모델의 과적합(Overfitting)을 방지하기 위한 Regularization 방법 중 하나이다.
작동방식은 드롭아웃을 실행하면 훈련이 반복되는 과정에 무작위로 레이어의 뉴런을 삭제하는 방식으로 동작한다.

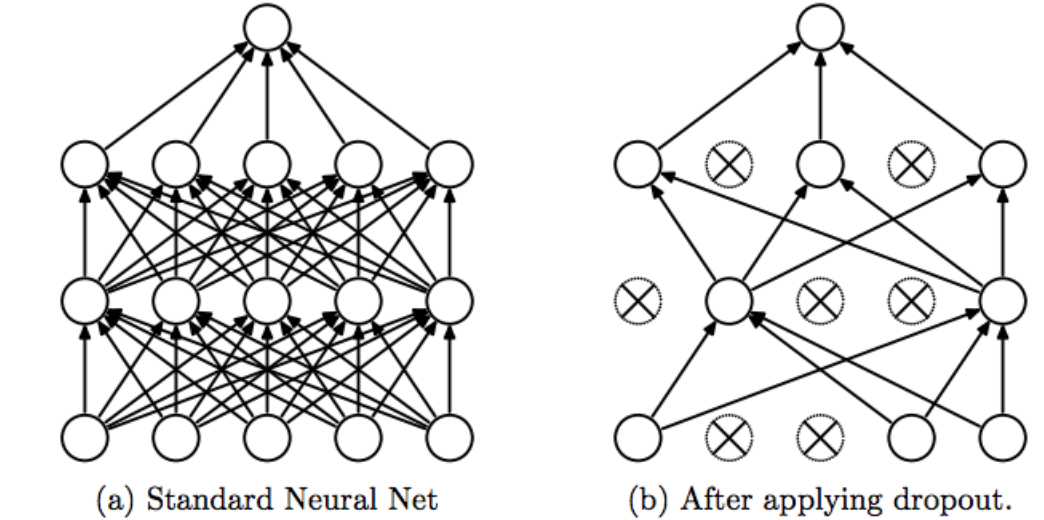
위 사진은 Dropout이 작동하는 방식을 나타낸 것이다.

Batch Normalization

배치정규화는 학습 효율을 높이기 위한 Regularization 방법 중 하나로 Dropout과 같이 과적합을 방지해준다.
과적합 방지 이외에도 아래와 같은 도움을 준다.

• 학습 속도를 개선
• 가중치 초기값 선택의 의존성을 낮춘다
• Gradient Vanishing 문제 해결

배치 정규화는 활성화 함수의 활성화 값 또는 출력값을 정규화 하는 작업으로 신경망의 각 layer에 배치(데이터) 분포를 정규화 하는 작업이다.
배치마다 정규화를 하기 때문에 전체 데이터에 대한 평균과 분산 값이 달라질 수 있고 학습 마다 활성화 값과 출력값을 정규화 하기 때문에 가중치 초기값(초기화)에서 자유로워진다.