✏️ 선형 회귀
✏️ 선형 회귀 모델의 정의
선형 회귀 모델은 입력 데이터의 특징 사이의 독립성을 가정하고, 데이터 특징에 대한 선형 결합으로 회귀 문제를 푸는 것을 의미한다. 이를 수식으로 표현하면 다음과 같다:
[ ]
여기서 ()는 예측값에 해당하고, )는 절편(혹은 편향)에 해당한다. 일반적으로 절편을 포함하는 것이 유리하다. 가중합으로 표현되는 다항식은 행렬 곱으로 간단하게 표현할 수 있다.
✏️ 비용 함수
선형 회귀에서는 목푯값과 예측값 사이의 차이를 측정하여 비용 함수를 정의한다. 두 값 모두 실수의 범위를 가지므로, 두 값 사이의 양적 차이(잔차)의 제곱 평균으로 평균 제곱 오차(Mean Squared Error, MSE)를 비용 함수 )로 정의할 수 있다:
]
선형 회귀는 잔차의 제곱값이 최소가 되는 파라미터를 찾는 작업이므로, 최소 제곱법(Ordinary Least Squares, OLS)이라고도 한다.
✏️ 최적화 방법론
비용 함수를 최소화하는 파라미터를 찾는 것이 최적화의 목적이다. 선형 회귀를 위한 최적화 방법에는 정규 방정식 풀이와 경사 하강법이 존재한다.
-
정규 방정식
- 파라미터 값 직접 계산
- 최소 값을 찾기 위한 미분값(도함수)이 0이 되는 점 계산
-
경사 하강법
- 비용 함 수가 작아지는 방향을 찾아 점차 파라미터를 조정하는 방법
✏️ 정규 방정식 (Normal Equation)
정규 방정식은 파라미터 값을 직접 계산하는 방법이다. 최소값을 찾기 위해 도함수가 0이 되는 점을 계산하며, 이를 통해 다음과 같은 식을 도출할 수 있다:
]
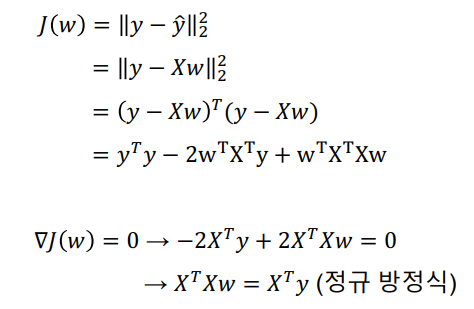
이때 )의 역행렬이 존재한다면, (w)의 유일한 해를 직접 구할 수 있다:
[ ]
정규 방정식의 시간 복잡도는 (O(p^3))이며, 일반적으로 (n \gg p)인 경우에 유용하다.
✏️ 경사 하강법 (Gradient Descent)
경사 하강법은 비용 함수가 작아지는 방향을 찾아 점진적으로 파라미터를 조정하는 방법이다. 임의로 설정한 초기 파라미터 값을 기준으로 비용 함수의 기울기(Gradient)를 계산하여, 기울기가 줄어드는 방향으로 파라미터를 수정 이동한다. 반복 수행으로 기울기가 0에 가까워지면 최적값에 도달한다.
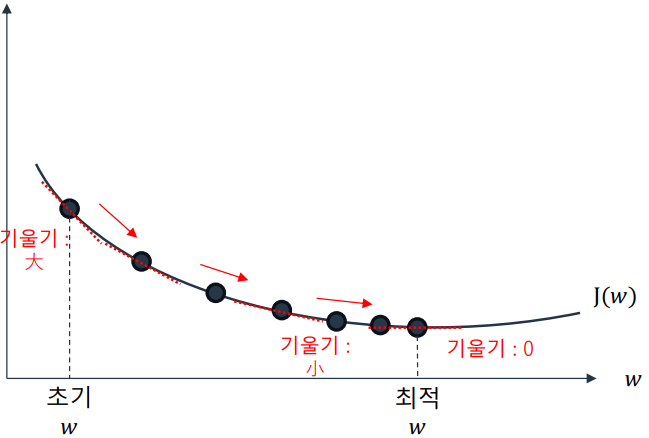
적절한 학습률(learning rate, lr)을 설정해야 하며, 값이 너무 작다면 최적화 소요 시간이 증가하고, 값이 너무 크다면 발산하거나 최적값에 도달할 가능성이 낮아진다.
경사 하강법의 파라미터 업데이트 수식은 다음과 같다:
[ ]
- 비용 함수를 통해 전체 비용을 구한다.
- 각 파라미터의 미분값을 구한다
- 현재 값을 기준으로 기울기가 작아지는 방향으로 이동한다.
- 적절한 학습률을 사용한다.
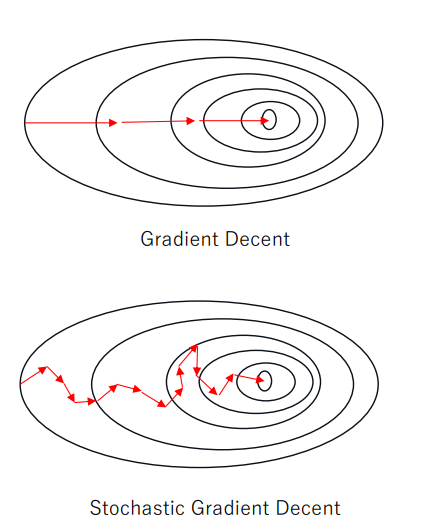
✏️ 확률적 경사 하강법 (Stochastic Gradient Descent, SGD)
확률적 경사 하강법은 경사 하강법과 달리 모든 학습 데이터를 사용하지 않고, 일부 데이터를 샘플링하여 경사 하강법을 진행하는 방법이다. 이를 통해 작은 데이터로 수정 이동을 반복하므로 빠른 수렴이 가능하다. 데이터가 많거나 특성이 많은 경우에 사용하기 용이하다. ( or
✏️ 어떤 최적화 방법론을 사용할까?
-
정규 방정식
- 튜닝한 변수가 없고, 해를 제공
- 특성 수가 많으면 복잡도와 메모리 문제 발생
- 훈련 세트가 크지 않을 때 빠르게 구하기 좋다
-
경사 하강법
- 특성 수와 샘플의 수에 민감도가 적다.
- 반복적인 연산 필요하며, 변수 최적화할 때마다 결과 영향 있음
✏️ 다중공선성 (Multicollinearity)
다중공선성은 입력 데이터의 특징값들 사이에 상관관계가 존재할 때 발생하는 문제 상황이다. 이로 인해 모델이 작은 데이터 변화에도 민감하게 반응하여 안정성과 해석력이 저하될 수 있다.
- 정규 방정식으로 해를 구하는 상황에서 치명적이다.
- ) 역행렬이 존재하지 않을 수 있다.
다중공선성을 해결하기 위해 특이값 분해를 이용한 SVD-OLS 방법이 존재한다. 이는 정규 방정식 해풀이에 사용되는 )의 역행렬 계산을 피하면서도 해를 구할 수 있는 방법이다.
✏️ SVD-OLS (Singular Value Decomposition - Ordinary Least Squares)
다중공선성 문제를 해결하기 위해 SVD-OLS 방법을 사용한다. 이 방법은 정규 방정식 해 풀이에서 발생하는 문제를 피하면서도 선형 회귀 모델의 해를 구할 수 있는 방법이다.
SVD-OLS 방식
-
특이값 분해(SVD)를 활용하여 학습 데이터 행렬 )를 분해한다:
]
-
특이값 분해된 입력 )에 OLS 방식을 적용하여 비용 함수 )를 최소화하는 파라미터 )를 구한다:
=
-
해를 구하는 과정에서 다음과 같은 식을 도출한다:
= -
시간 복잡도는 )이다:
[ n: 입력 데이터 수 / p: 사용하는 특성의 수]
비교: SVD-OLS vs. 단순 OLS
-
단순 OLS 기반의 해:
-
SVD-OLS 방식의 해:
SVD-OLS에서는 )의 역행렬 계산이 필요하지 않다. 다중공선성이 크게 존재하는 경우 )가 특이 행렬이 되거나 특이 행렬에 가까워지면 역행렬을 계산할 수 없다. 이때 SVD-OLS 방식을 사용하면 해결할 수 있다. 단, SVD 계산으로 인한 시간 소요가 증가할 수 있다.
SVD-OLS 방법은 Scikit-learn 패키지의 선형 회귀 알고리즘에서도 구현되어 있다. 이는 다중공선성이 있는 데이터에 대해 더욱 안정적이고 신뢰성 있는 해를 제공할 수 있다.
✏️ 규제 (Regulation)를 사용하는 선형 모델
과적합 문제(over-fitting)
- 머신러닝 모델이 피해야하는 모델
- 모델이 학습 데이터에 너무 집중해 일반화가 떨어지는 상황
- 과적합 발생 시 파라미터인 w의 값이 매우 커지게 된다
- 따라서 w의 값이 너무 커지지 않도록 규제를 해야함
과적합 문제를 해결하기 위해 규제를 추가한 선형 모델들이 있다. 라쏘 회귀(Lasso Regression)와 릿지 회귀(Ridge Regression)가 대표적이다.
라쏘 회귀 (Lasso Regression)
라쏘 회귀에 사용되는 L1 규제는 일부 파라미터의 값을 완전히 0으로 만들 수 있다. 이를 통해 모델이 사용하는 데이터 특성 중 불필요한 특성을 무시하는 효과를 가져올 수 있다.
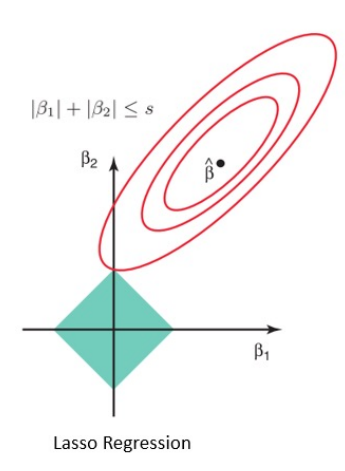
-
변수가 많고, 일부 변수가 중요한 역할을 쓸 때 활용
릿지 회귀 (Ridge Regression)
릿지 회귀에 사용되는 L2 규제는 파라미터 값을 적당히 작게 만든다. 이는 입력으로 받는 데이터의 모든 부분을 이용해 출력을 판단하는데 사용되며, 모든 특성이 출력 결과에 적당히 영향을 미치는 경우에 유용하다.
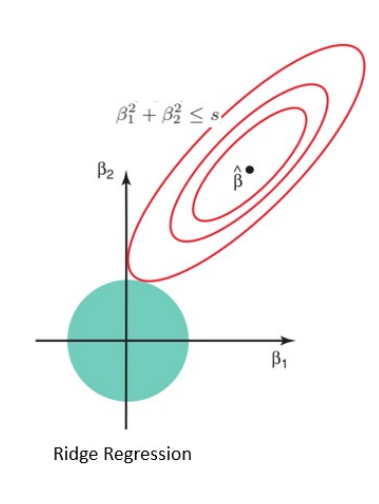
- 모든 특성이 출력 결과에 영향을 미칠 때 활용
