Machine Learning (5) - 선형 분류

✏️ 선형 분류

✏️ 로지스틱 회귀(Logistic Regression)

로지스틱 회귀는 이진 분류 문제를 해결하기 위한 기본 알고리즘 중 하나로, 입력 데이터가 특정 클래스에 속할 확률을 예측하는 모델이다. 예를 들어, 이메일이 스팸인지 아닌지를 분류하는 문제에 사용될 수 있다.

확률이 갖는 값의 범위가 0~1의 실수값이기 때문에, 확률을 직접적으로 예측하는 방식으로 문제를 해결한다.

• 분류 문제를 풀지만 회귀 방식으로 문제를 접근
• 예측한 특정 클래스 확률 값이 일반적으로 50% 이상이면 해당 클래스에 속한다고 예측 ( positive or negative )
  

---

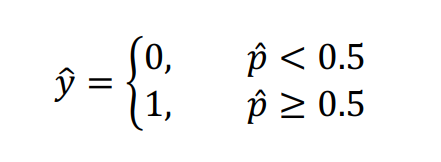
✏️ 로지스틱 함수 (Logistic Function)

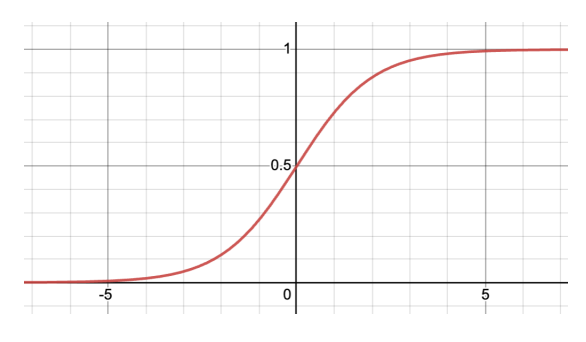
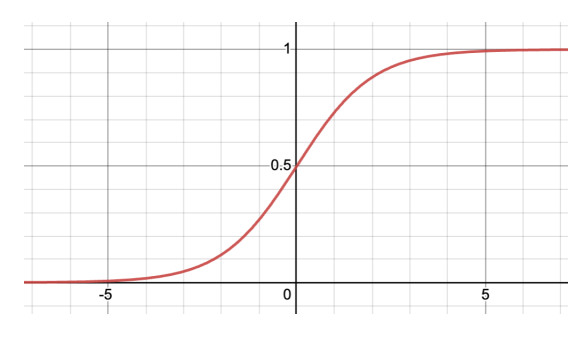
로지스틱 회귀는 입력 데이터와 가중치의 선형 결합에 로지스틱 함수를 적용하여 결과를 예측한다. 로지스틱 함수는 다음과 같은 형태를 가진다:

$\sigma(x) = \frac{1}{1 + e^{-x}}$

이 함수는 입력 값이 어느 클래스에 속할 확률을 출력하며, 출력 값은 항상 0과 1 사이의 값을 갖는다.

✏️ 로짓 (Logit)과 오즈 (Odds)

• 오즈 (Odds): 특정 사건이 발생할 확률 (p)와 발생하지 않을 확률 (1 - p)의 비율이다.

  $\text{odds} = \frac{p}{1 - p}$

• 로짓 (Logit): 오즈에 로그 함수를 적용한 값이다.
  $\text{logit} = \log \left( \frac{p}{1 - p} \right)$

로지스틱 회귀에서는 로짓 값을 사용하여 데이터를 선형 결합한 후, 이를 로지스틱 함수에 적용하여 예측 확률을 계산한다.

✏️ 로짓 유도

https://devhwi.tistory.com/18

✏️ 일반 회귀가 아닌 로지스틱을 사용하는 이유?

• 선형 모델은 독립변수의 션형 변환에 따라 종속 변수의 관계를 알아본다.
• 하지만 확률 입장에서 변화향이 구간에 따라 다른 의미를 가질 수 있다. ex) 0.49 <-> 0.50, 0.98 <-> 0.99
• 즉 출력 결과의 해석이 선형적이지 않을 수 있다.
• 이를 위해 선형적일 수 있는 $logit$을 사용
  

✏️ 비용 함수 (Cost Function)

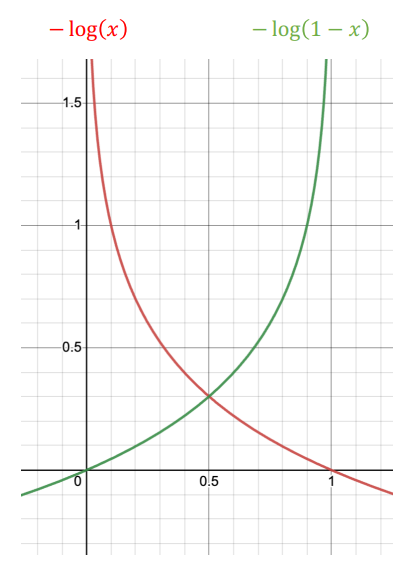
로지스틱 회귀에서는 정답과 예측 값 사이의 차이를 측정하기 위해 로그 손실(log loss) 비용 함수를 사용한다. 비용 함수는 다음과 같다:

$J(w) = -\frac{1}{N} \sum_{i=1}^{N} \left( y_i \log(\hat{p}_i) + (1 - y_i) \log(1 - \hat{p}_i) \right)$

여기서 $(y_i$)는 실제 값이고, $(\hat{p}_i$)는 예측 확률이다. 이 비용 함수를 최소화하는 파라미터 ($w$)를 찾는 것이 목표이다.

✏️ 경사 하강법 (Gradient Descent)

로지스틱 회귀에서도 경사 하강법을 사용하여 비용 함수를 최소화하는 파라미터를 찾는다. 경사 하강법은 비용 함수의 기울기를 계산하여 파라미터를 업데이트하는 방식으로 작동한다. 업데이트 수식은 다음과 같다:

$w^{new} = w - \alpha \frac{\partial J(w)}{\partial w}$

여기서 $(\alpha$)는 학습률(learning rate)이며, 기울기 $(\frac{\partial J(w)}{\partial w})$는 비용 함수의 기울기를 의미한다.