✏️ K-means Clustering
✏️ K-means Clustering이란?
K-means Clustering, 또는 K-평균 군집화는 비지도 학습법으로, 전체 데이터를 K개의 클러스터로 나누는 기법이다. 방법이 간단하며 효과적이고, 결과 해석이 쉬워 많은 분야에서 사용된다.
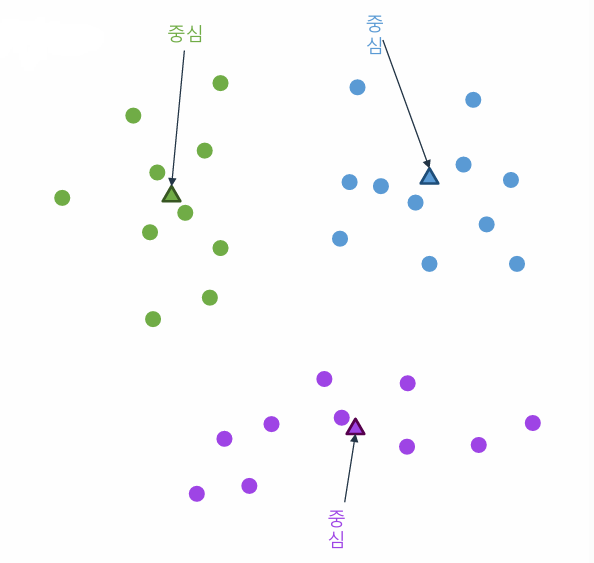
- 클러스터: 데이터가 그룹화된 단위.
- 중심점: 각 클러스터의 중심으로, 해당 클러스터에 속한 데이터들의 평균값을 나타낸다.
✏️ K-means Clustering 과정
K-means 군집화 기법을 푸는 주요 알고리즘으로는 로이드(Lloyd) 알고리즘과 엘칸(Elkan) 알고리즘이 있다. 로이드 알고리즘은 가장 기본적인 방법으로, 다음 네 가지 단계로 구성된다.
(1) 초기화
먼저, K개의 클러스터 중심점을 임의로 선택한다. 초기 중심점의 선택은 최종 결과에 큰 영향을 미칠 수 있으며, 따라서 초기화 방법이 중요하다.
- 임의 초기화: 무작위로 K개의 중심점을 선택한다.
- k-means++ 초기화 방법: 첫 번째 중심점을 무작위로 선택하고, 이후의 중심점은 현재 선택된 중심점들과의 거리가 최대가 되는 데이터 포인트를 선택하는 방식으로 진행한다. 이는 초기 중심점이 멀리 떨어지도록 하여 군집화 성능을 향상시킨다.
(2) 할당
각 데이터 포인트를 가장 가까운 클러스터 중심에 할당한다. 일반적으로 유클리드 거리(Euclidean Distance)를 사용하여 각 데이터 포인트와 클러스터 중심 간의 거리를 계산한다.
]
- 유클리드 거리: 두 점 사이의 직선 거리를 의미한다. 대부분의 경우 유클리드 거리가 사용되지만, 특정 상황에서는 다른 거리 측정 방법도 사용될 수 있다.
- 코사인 유사도 (Cosine Similarity): 두 벡터의 코사인 값을 이용하여 유사도를 측정.
- 맨해튼 거리 (Manhattan Distance): 두 점 사이의 수직 및 수평 거리의 합으로 계산.
(3) 업데이트
각 클러스터에 속한 데이터 포인트들의 평균 위치를 계산하여 클러스터 중심의 위치를 업데이트한다. 이 단계는 클러스터의 중심점이 현재 클러스터에 속한 모든 데이터 포인트의 평균으로 이동하는 과정이다.
- 중심점 업데이트: 각 클러스터의 중심점은 해당 클러스터에 속한 모든 데이터 포인트의 평균값으로 갱신된다.
[]
여기서 ()는 클러스터 ()의 새로운 중심점이고, ()는 클러스터 ( i )에 속한 데이터 포인트들의 집합이다.
(4) 반복
클러스터 중심의 변화가 미미할 때까지 할당 과정과 업데이트 단계를 반복한다. 변화가 미미하다는 것은 다음과 같은 조건 중 하나를 만족할 때이다:
- 클러스터 중심의 위치 변화가 거의 없거나,
- 클러스터에 할당되는 데이터 포인트의 변화가 없거나,
- 동일한 데이터 포인트 할당 과정이 반복되거나,
- 지정된 반복 횟수에 도달하거나.
이러한 조건을 만족하면 알고리즘은 수렴(convergence)한다고 말하며, 최종 클러스터링 결과를 제공한다.
✏️ 엘보우 방법 (Elbow Method)
엘보우 방법은 적절한 클러스터 수(K)를 선택하기 위한 방법론으로, 다양한 K 값을 시도하며 클러스터링 성능을 측정한다. 일반적으로 Sum of Squared Errors (SSE) 값을 사용하여 성능을 평가한다.
- SSE (Sum of Squared Errors): 각 클러스터 내의 데이터 포인트와 클러스터 중심 간의 거리의 제곱합으로, 데이터 포인트가 클러스터 중심에 얼마나 가까운지를 나타낸다.
여기서 ( )는 클러스터 ( ), ()는 클러스터 ( )의 중심점이다.
- 엘보우 포인트: 그래프 상에서 SSE의 감소율이 급격히 줄어드는 지점을 최적 클러스터 수(K)로 간주한다. K가 증가함에 따라 SSE는 감소하지만, 어느 순간부터 감소율이 둔화되기 시작한다. 이 지점이 마치 팔꿈치(elbow)처럼 보이기 때문에 엘보우 포인트라고 부른다.
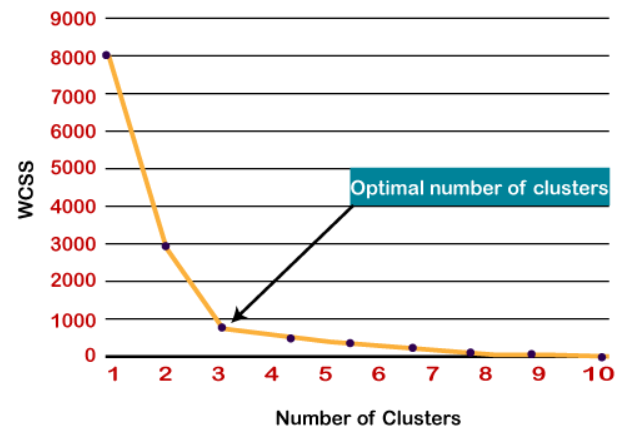 https://nicola-ml.tistory.com/66#google_vignette
https://nicola-ml.tistory.com/66#google_vignette
엘보우 방법은 클러스터 수를 결정하는 데 유용하지만, 항상 명확한 엘보우 포인트가 존재하지 않을 수 있다. 이러한 경우, 실루엣 계수(Silhouette Coefficient)와 같은 다른 평가 지표를 함께 사용하여 최적의 클러스터 수를 결정할 수 있다.
✏️ 실루엣 계수 (Silhouette Coefficient)
클러스터링의 품질을 평가하는 방법으로, 클러스터 안의 응집도와 서로 다른 클러스터 간의 분리도를 동시에 고려한다. 이 값은 -1에서 +1 사이의 값을 가지며, 높은 값일수록 좋은 클러스터링을 의미한다.
 https://medium.com/@cmukesh8688/silhouette-analysis-in-k-means-clustering-cefa9a7ad111
https://medium.com/@cmukesh8688/silhouette-analysis-in-k-means-clustering-cefa9a7ad111
- x축: 실루엣 계수 값 (-1에서 1 사이).
- y축: 데이터 포인트 인덱스, 각 클러스터별로 나누어 표시.
- 실루엣 폭: 각 데이터 포인트의 실루엣 계수를 나타내는 막대의 길이. 폭이 넓을수록 클러스터링이 잘된 것을 의미.
- 평균 실루엣 계수 선: 전체 데이터의 평균 실루엣 계수를 수직선으로 표시. 이 값이 높을수록 클러스터링이 잘된 것을 의미.
실루엣 계수, s(i):
[ ]
- 최대값: 1 → ()가 거의 0에 가까워 ()만 남는 상황.
- 최소값: -1 → () 값이 작아지고 ()가 커지는 경우.
실루엣 계수는 Elbow Method와 함께 사용하여 최적의 K 값을 찾는 데 도움이 된다.
✏️ 어떤 방법을 사용할지
- 엘보우 방법: 빠르고 직관적인 초기 평가가 필요할 때 유용하다. 특히 데이터셋이 작거나 중간 크기일 때 적합하다.
- 실루엣 계수: 클러스터링 품질을 보다 정확하고 객관적으로 평가하고자 할 때 유용하다. 특히 데이터셋이 크거나 클러스터 간의 명확한 비교가 필요할 때 적합하다.
