Machine Learning (7) - Decision Tree

✏️ Decision Tree

✏️ Tree 용어

노드 (Node)

• 루트 노드 (Root Node): 트리의 가장 상단에 위치한 노드로, 분류 또는 예측을 시작하는 지점.
• 분할 노드 (Decision Node): 데이터를 더 작은 하위 집합으로 나누는 데 사용되는 중간 노드.
• 리프 노드 (Leaf Node): 트리의 말단에 위치한 노드로, 더 이상의 분기가 없고 자식 노드를 갖지 않음.

엣지 (Edge)

• 노드와 노드를 연결하는 선으로, 상위 노드의 특정 질문에 대한 가능한 답변을 나타냄.
  
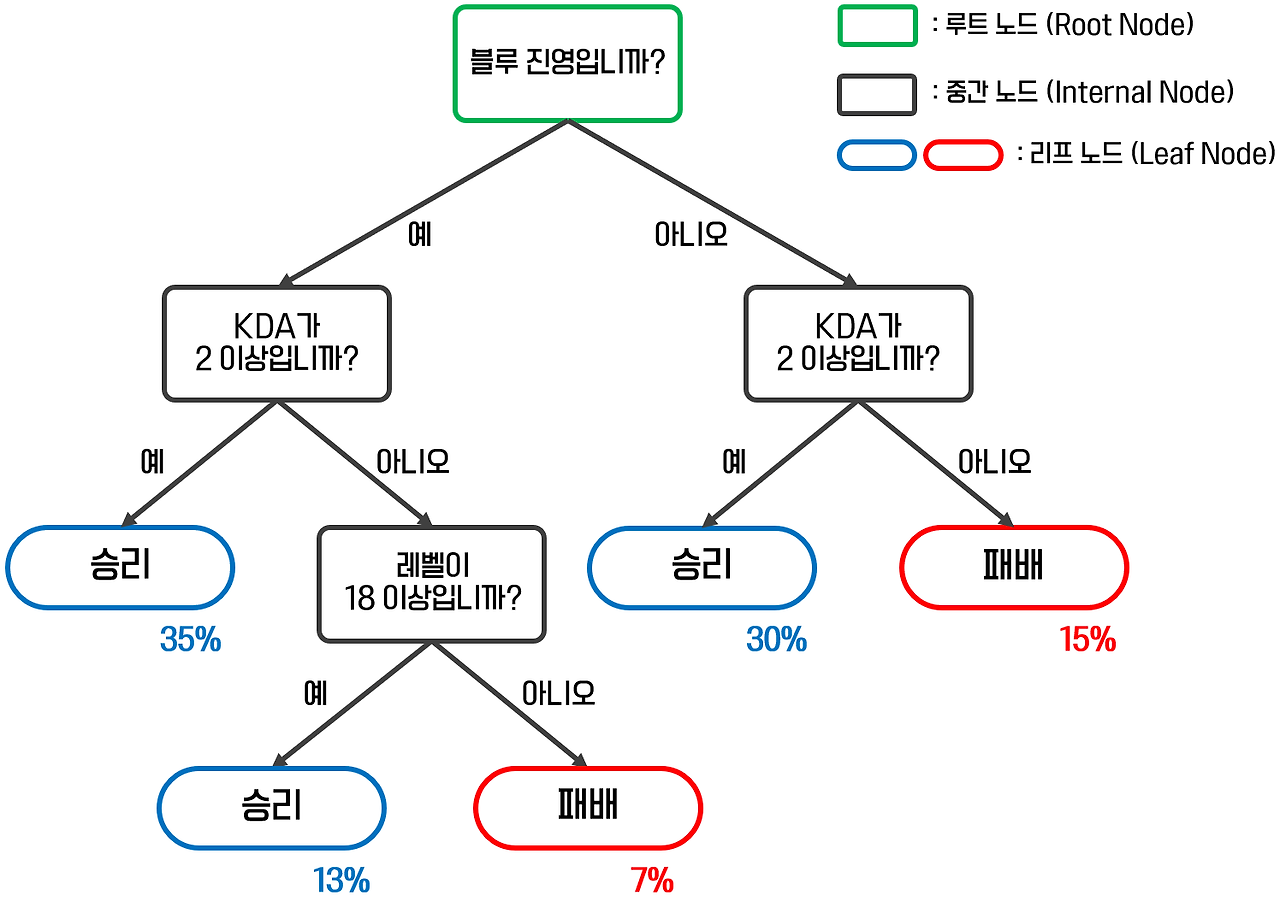
  https://leehah0908.tistory.com/13

✏️ 분류 문제를 위한 Decision Tree

✏️ 결정 기준 (Decision Criteria)

1. 정보 이득 (Information Gain)

   • 엔트로피를 기반으로 데이터 분할의 순도를 측정하는 방법.

   • 엔트로피(Entropy): 불확실성을 의미하며, 포함하는 정보의 양과 반비례.

     • 엔트로피가 크면 불확싱성이 크고, 정보량이 적다.

   • 엔트로피 계산:

     [ $H(X) = - \sum P(x_i) \log P(x_i)$ ]

     • ($-$)를 부여하는 이유는 확률(0~1)이 log 안에서 들어가면 음수가 되기 때문에, 다시 log 값을 양수로 만들기 위함

   • 정보 이득: 부모 노드와 자식 노드들의 엔트로피 차이로, 엔트로피가 낮아지는 방향으로 결정 경계를 선정.

     [ $\text{InfoGain} = \text{Entropy(parent)} - \sum \left( \frac{|child|}{|parent|} \times \text{Entropy(child)} \right)$ ]

2. 지니 불순도 (Gini Impurity)

   • 데이터 집합의 순도를 측정하는 또 다른 방법.
   • 지니 불순도 계산:
     [ $\text{Gini}(S) = 1 - \sum (p_i)^2$ ]
   • 0 이상 1 미만의 값을 가지며, 0에 가까울수록 순도가 높고, 1에 가까울수록 불순도가 높음.
     

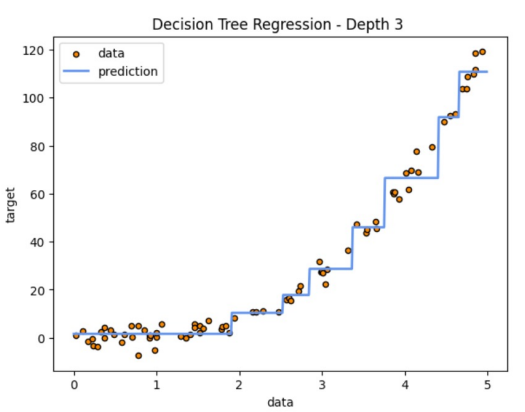
몇 차례 씩 Depth가 깊어지면, 계단 형태로 오차를 최소화하는 방향으로 Tree가 만들어진다.

✏️ 회귀 문제를 위한 Decision Tree

MSE 최소화 방식

회귀 문제에서 Decision Tree는 각 노드에서 실제 값과 예측 값 사이의 평균 제곱 오차(MSE)를 계산하고, 이 값을 최소화하는 노드를 찾아 트리를 생성한다.

[ $\text{MSE} = \frac{1}{N} \sum_{i=1}^{N} (y_i - \hat{y}_i)^2$ ]

✏️ Decision Tree 사용 시 주의사항

• 해석 용이성: 트리 구조는 직관적이고 해석이 용이함.
• 스케일링에 둔감: 데이터의 스케일링에 크게 영향을 받지 않음.
• 노이즈에 민감: 데이터 노이즈에 매우 민감하여, 특정 데이터의 추가가 전체 모델 결과에 큰 변화를 줄 수 있음.
• 과적합의 위험: 트리의 깊이가 깊어질수록 과적합의 위험이 큼.
• 축에 수직인 데이터 분할: 트리 모델은 축에 수직으로 데이터를 분할하므로, 경계면이 회전된 데이터에 대해 구불구불한 경계면이 생성될 수 있음.