[CV] 모델 양자화(quantization)를 통해 성능 높이기

Kwanni·2025년 8월 6일

Computer Vision

목록 보기

3/3

들어가며

객체 탐지 모델인 YOLO를 학습했고, 탐지한 객체를 추적하기 위해 Tracking 기술 중 ByteTrack을 사용하여 동일한 객체를 추적했다. 이번 프로젝트에서 좋은 기회로 NPU 서버를 사용할 수 있게 되어, YOLO 모델을 NPU를 통해 추론해보려 한다. NPU를 이용한 추론은 모델의 실행 성능과 효율성을 높이기 위해 양자화(quantization) 기술을 적용해야 한다. 모델 양자화는 처음 접하는 기술인데, 이번 블로깅에서는 NPU를 활용해 추론하는 과정을 자세히 다뤄보고자 한다.

개요

본 내용에 들어가기에 앞서, 대부분 AI 모델 학습을 가속화하기 위해 GPU를 사용한다는 이야기는 많이 들어봤을 것이다. 하지만 NPU는 다소 생소할 수 있어서, 간단히 짚고 넘어가려 한다.
NPU(Neural Processing Unit)는 AI 및 딥러닝 알고리즘을 효율적으로 실행하기 위해 설계된 하드웨어 장치다. NPU는 그래픽 처리, 병렬 연산, AI 가속 등 다양한 용도로 활용되는 GPU와 달리, 오직 AI와 딥러닝 신경망 연산에 특화되어 있다. 그래서 더 적은 전력으로, 더 빠르고 효율적인 연산이 가능하다. 이때 꼭 필요한 기술이 바로 '양자화'다.

확장자 변경

furiosa의 warboy라는 NPU를 사용했고, NPU를 통해 추론을 하려면 모델을 .pt 확장자가 아닌 .onnx 확장자로 변환해야 한다.

from ultralytics import YOLO

model = YOLO("yolov8x.pt")

model.export(
    format="onnx",
    imgsz=1280,      
    opset=13,            
    dynamic=False        
)

imgsz는 학습할 때 사용했던 이미지 크기로 맞춰주었다.

YOLO 구조 확인

onnx 확장자로 모델을 변환했고, 프로젝트에서 선정한 YOLO의 구조를 살펴보자. Netron에서 onnx 확장자 모델을 업로드하면 모델의 구조를 시각적으로 확인할 수 있다.

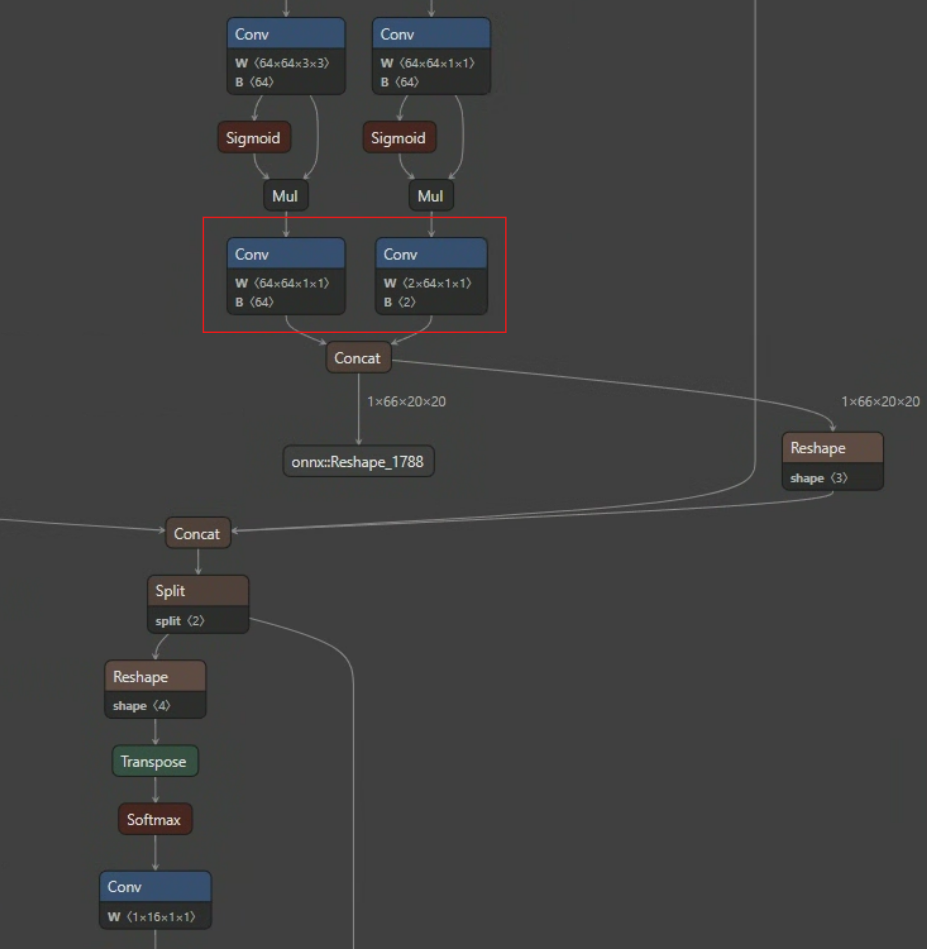
YOLO는 출력 부분에서 object box 처리와 class 분류를 담당한다. 이미지에서 빨간색 네모로 나타낸 부분이 바로 object box와 class를 분류하는 층이다. 왼쪽 박스가 object box를 결정하는 부분이고, 오른쪽 박스가 class를 분류하는 부분이다. 이 모델은 두 가지 class를 분류하도록 설계되어 있어서, Bias 값이 2로 표시되는 것을 볼 수 있다.

그 이후에는 후처리 과정이 진행된다. 이는 최종 출력 포맷으로 결과를 만들어주는 단계다. 양자화를 적용할 때, 이 후처리 부분은 비학습 연산이기 때문에 별도로 처리해줘야 한다.

양자화 전 후처리(Postprocessing)

YOLO 모델은 object box와 class를 출력한 뒤, 후처리 단계가 추가로 필요하다. 신뢰도 계산이나 좌표 변환 등 수학적 연산이 여기에 포함되고, 조건에 따라 NMS(Non-Maximum Suppression) 연산도 실행된다.
NMS는 같은 객체에 대한 중복된 object box를 제거해주는 알고리즘이다. 이런 후처리 연산들은 CPU에서 처리하는 것이 더 효율적이기 때문에, NPU로 추론을 진행한 다음 다시 코드로 후처리를 해주는 방식이 적합하다.

후처리 부분이 최적화된 모델 구조는 아래 이미지와 같이 바뀐다.

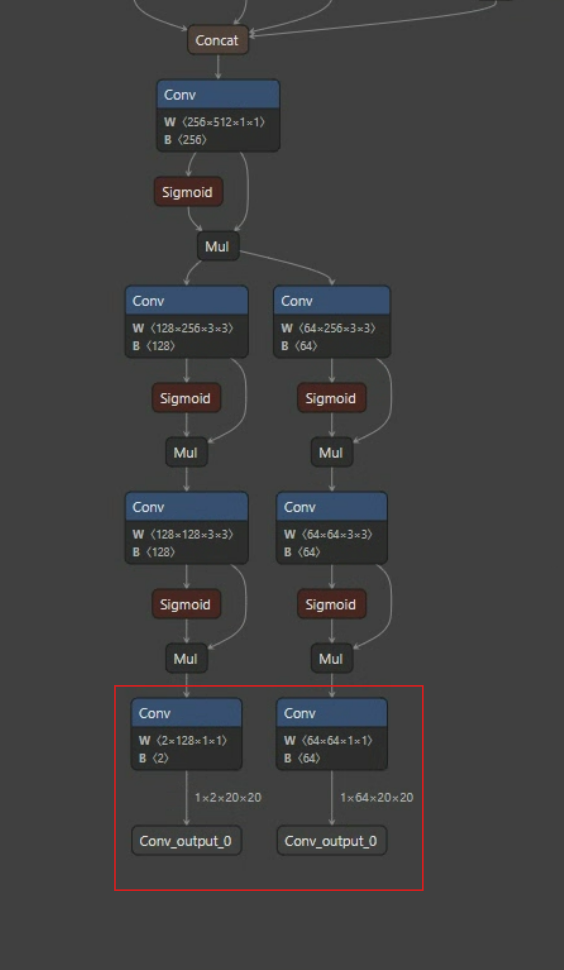
출력 이후 후처리 단계가 모델 내부에서 빠진 것을 확인할 수 있다.

양자화(Quantization)란?

양자화란 인공지능 모델 실행의 부담을 줄이기 위한 기술이다. 신경망의 가중치와 활성화 함수 출력을 더 작은 비트 수로 표현하도록 변환하는 과정이다.

양자화를 왜 쓰는가?

기존 모델의 값들은 대부분 32비트 부동소수점(FP32) 형식인데, 양자화를 적용하면 8비트 정수(INT8) 등 더 적은 비트의 자료형으로 변환할 수 있다. 즉, 모델의 계산 및 저장 자원(메모리 사용량)이 크게 줄어든다.

대부분의 모델 학습은 TensorFlow와 PyTorch를 사용해서 진행된다.
아래는 공식 문서와 코드에서 기본 자료형이 Float32임을 확인한 예시다.

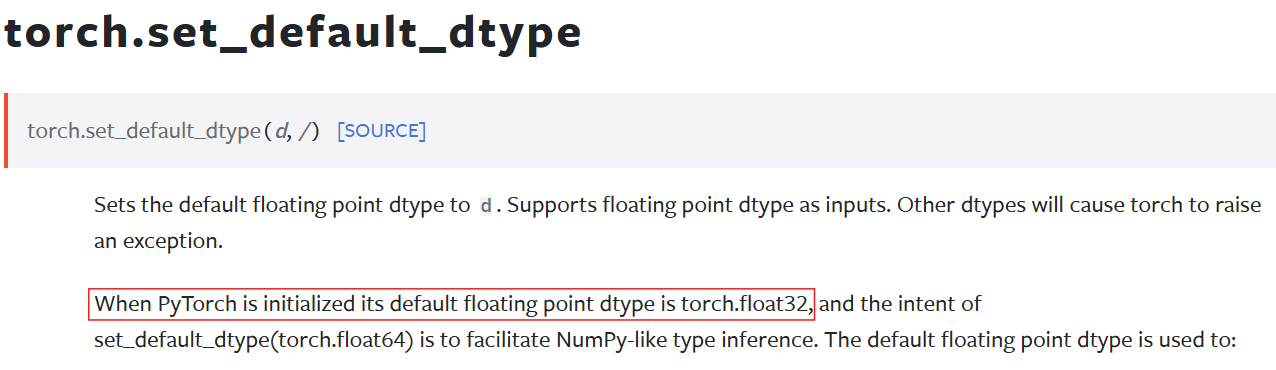
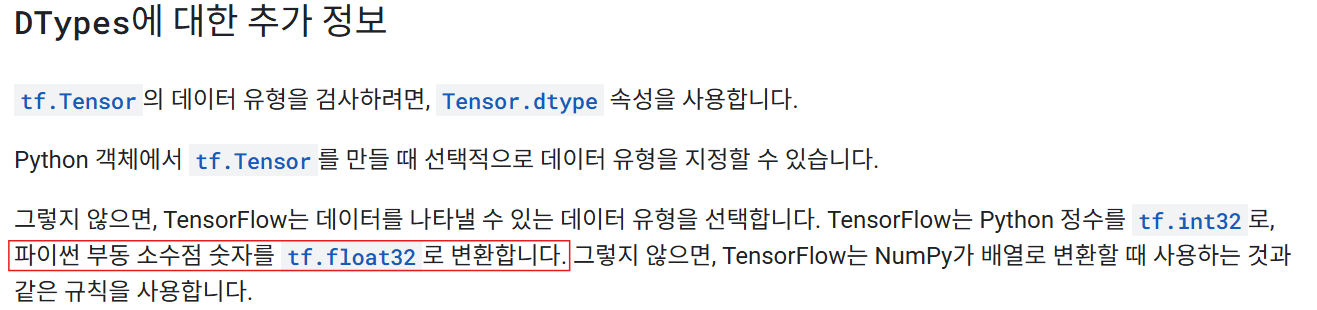
양자화 덕분에 추론 속도가 최대 2~4배까지 빨라질 수 있다.
계산량이 감소해서 전력 소모도 줄고, 그만큼 배터리 수명도 늘어난다.
모델이 경량화되어 배포와 운영이 훨씬 유연해진다.

이처럼 양자화에는 다양한 장점이 있다.

양자화 과정

$q = \mathrm{clip}\left(\mathrm{round}\left(\frac{r}{s}\right) + z,\ Q_\text{min},\ Q_\text{max}\right)$

기호	의미 설명
$q$	양자화된 정수값 (quantized integer value)
$r$	입력 실수값 (원본 float value)
$s$	스케일링 인자 (scale, 실수→정수 변환 비율)
$z$	제로포인트 (zero point, 실수 0의 정수 위치)
$Q_{min}$	정수의 최소값 (예: int8은 -128)
$Q_{max}$	정수의 최대값 (예: int8은 127)
$\operatorname{clip}$	범위 밖의 값은 최소/최대로 잘라줌
$\operatorname{round}$	가장 가까운 정수로 반올림

양자화 공식과 변수들에 대해 정리했다.
간단히 말하면, 실수 $r$ 값을 양자화 연산을 통해 정수 $q$ 값으로 변환하는 것이다.
이 과정에서 실수에서 정수로 변환하는 비율인 스케일( $s$ )과, 실수 0이 정수 영역에서 어디에 위치하는지를 나타내는 제로포인트( $z$ )도 함께 계산해야 한다.

제로포인트 $z$ 에 대해 예시를 들어 설명하겠다.

$z = \mathrm{round}\left(Q_{\text{min}} - \frac{r_{\text{min}}}{s}\right)$

예를 들어, 실수 값의 범위가 -3.0부터 3.0까지이고, int8로 양자화한다고 가정하자.
이때 정수 값의 범위는 -128부터 127까지이다.
실수 0은 이 범위에서 중앙값에 해당하므로, 정수형 범위에서도 0에 정확히 대응한다.

반면에, 실수 값의 범위가 -5.2부터 9.7까지라면 실수 0은 이 범위에서 중앙이 아니다.
따라서 정수형 범위에서 실수 0이 대응할 위치를 다시 매핑해줘야 한다.
위 공식에 값을 대입하면, 실수 0은 정수 -39에 대응되는 것을 알 수 있다.

그럼 왜 실수 0을 정확히 처리하는 것이 중요할까?

실수 0은 신경망 연산에서 중립적이며 기준이 되는 값이다.
학습과 추론 과정에서 0이 자주 등장하는데, 이 값이 정수 영역에서 잘못 매핑되면 전체 출력에 치명적인 영향을 줄 수 있다.
양자화의 목표는 실수 값을 정수 값으로 변환하면서 오차를 최소화하는 데 있는데,
실수 0이 정수 0 위치에 정확히 대응하면 필연적으로 수식상의 오차 또한 최소화된다.

실수(32-bit float) 기반 모델을 정수(INT8 등)로 변환할 때 발생할 수 있는 정확도 손실을 최소화하려면, 반드시 보정(calibration) 과정이 함께 이루어져야 한다.

보정 범위 계산(Calibration Method)
보정용 데이터셋 구성(Calibration Dataset)

보정용 데이터셋은 실제 레이어 출력 값의 범위를 관찰하기 위한 용도로, 학습에 사용했던 데이터 중 임의로 100~200개 정도를 사용하면 충분하다.
보정 범위 계산 방법은 furiosa에서 제공하는 방식을 참고하여 활용했다.

방법	분류	설명
MIN_MAX	비히스토그램 기반	값의 최소/최대만 사용, 속도는 빠르지만 정확도는 다소 낮을 수 있음
ENTROPY	히스토그램 기반	KL Divergence 기반, float와 int 분포 차이를 최소화하는 방식
PERCENTILE	히스토그램 기반	상하위 극단값을 제외(예: 0.1~99.9%), 더 안정적인 보정 값 제공
SQNR	히스토그램 기반	Signal-to-Quantization-Noise-Ratio(양자화 잡음비) 최대화를 목표로 하는 방식
MSE	히스토그램 기반	Mean Squared Error(평균 제곱 오차) 최소화, 손실을 최소로 억제하는 데 중점

각 방법은 데이터 분포와 요구 조건에 맞게 선택할 수 있다.

추론

양자화된 모델을 사용해 NPU에서 추론을 진행했다. 추론은 오직 NPU에서 수행하고, 사전에 최적화해둔 후처리 과정은 별도의 코드로 작성해, 추론이 끝난 뒤 CPU에서 연산하도록 구현했다.

NPU에서 추론한 결과와 GPU(RTX4060ti)에서 추론한 결과를 비교해보았다. 성능 비교를 위해 데이터셋은 NPU와 GPU 모두 동일한 1,500장을 사용했다.

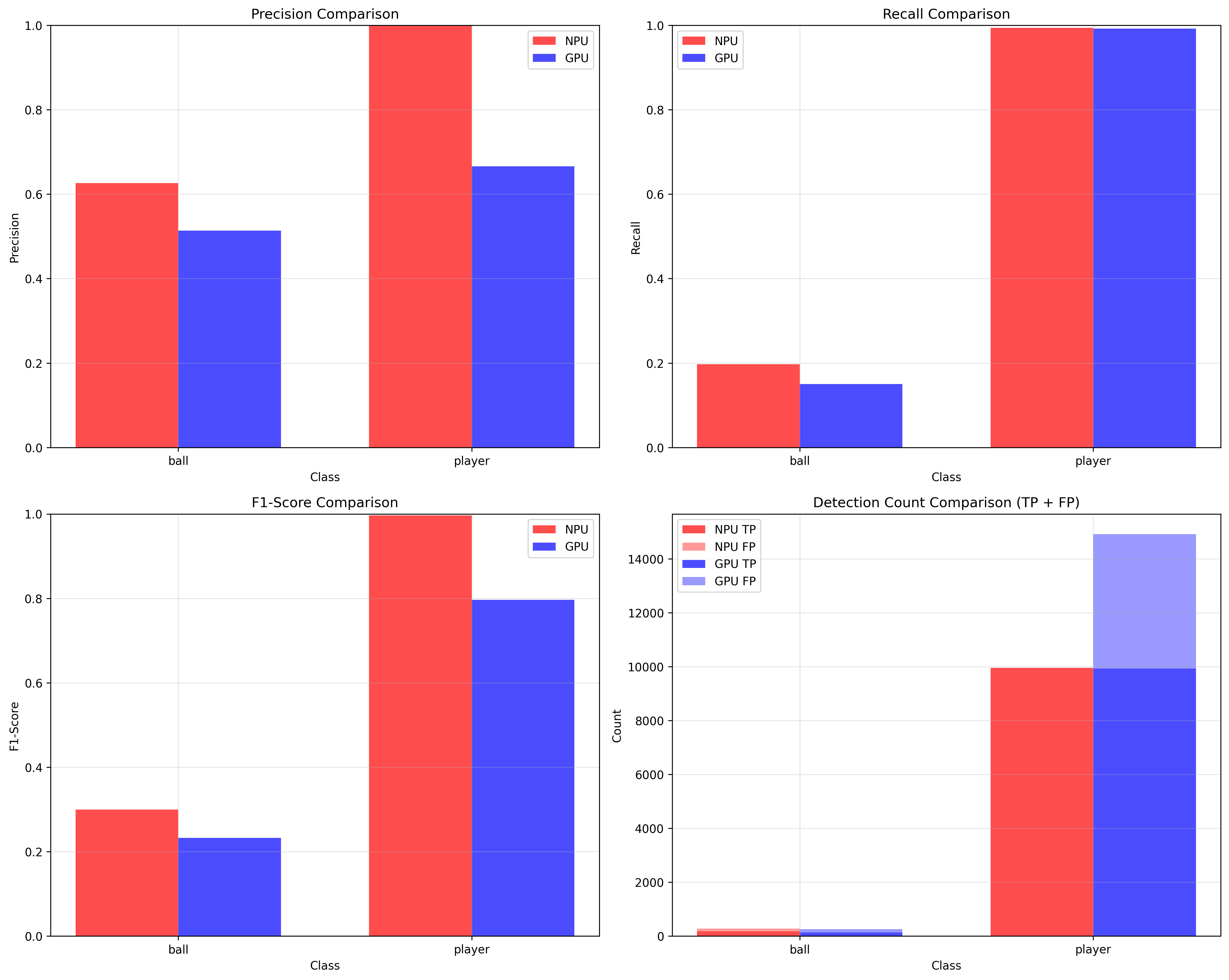
성능 비교 결과 해석

정밀도(Precision)
- 두 클래스(공, 선수) 모두에서 NPU가 GPU 대비 더 높은 정밀도를 달성했다.
- 특히 'player(선수)' 클래스에서는 NPU의 정밀도가 1에 육박하여 검출 신뢰도가 매우 높았다.
재현율(Recall)
- 'player(선수)' 클래스에서는 NPU와 GPU 모두 재현율이 1로, 검출해야 할 선수를 거의 모두 잡아냈다.
- 'ball(공)' 클래스에서는 두 환경 모두 상대적으로 낮은 재현율을 보이나, NPU가 GPU보다 소폭 높다.
F1-score
- 'player(선수)' 클래스에서 NPU가 GPU에 비해 월등히 높은 F1 점수를 기록함(1에 근접).
- 'ball(공)' 클래스에서도 NPU가 더 높다.
탐지 개수(TP+FP)
- 'player' 클래스의 경우 True Positive(TP)가 NPU가 약 10,000건, GPU는 약 15,000건.
  - False Positive(FP)는 GPU가 더 많아서, 오히려 NPU가 불필요한 오검출이 적다.
- 'ball' 클래스에서는 두 환경 모두 탐지 건수가 적으며, NPU가 FP도 가장 적음.