이진인덱스트리
흔히 계속 변하는 배열의 부분합을 구할때
FOR i N to M
으로 복잡도 O(n) 으로 구할수도 있겠지만,
이런 자료구조의 궁극적 사용 목표는 빠르게 하기 위해서 이다.
보통 이럴때 세그먼트 트리를 사용하는데,
0부터 N까지의 합 을 구할때는 세그먼트 트리보다 구현이 간단하면서 빠른
이진 인덱스 트리를 사용하게 된다.
(세그먼트 트리는 N부터 M 까지)
1부터 8까지의 배열이 있다고 가정한다면
이진 인덱스 트리는 다음과 같이 생겼다.
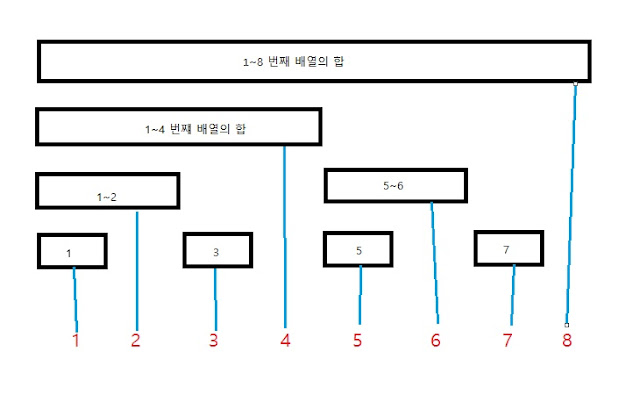
이진인덱스 트리는 배열로 구현하며
0번째는 사용하지 않는다.( 이유는 뒤에서 설명한다)
V={} 를 어떠한 배열이라고 하고, 우리는 V의 부분합을 구할 것이다.
이진인덱스트리를 E라고 표기한다.
E[1] 는 V의 첫 원소부터 첫원소까지의 합을 저장한다.
E[2]는 V의 첫원소부터 두번째 원소까지의 합을 저장한다.
E[4] 는 V의 첫원소부터 4번째 원소까지의 합을 저장한다.
예를들어 5까지의 합을 구하려 한다면
1~4 까지의 합 + 5의 합 을 더해주면된다.
그림으로 보면 E[4]+E[5] 가된다.
4 는 2진수로 0100 이고
5는 2진수로 0101 이므로
5를 먼저 결과값에 더하고, 5의 맨 오른쪽에 있는 1의 비트 값만큼 빼면된다.
그 인덱스가 0이 될때까지 반복하면 된다.
4의 맨 오른쪽 1 비트는 100 이고 이를 빼면 0이되므로 본 합 계산을 완료한다.
맨 오른쪽 비트 찾는 공식은 A & -A 연산으로 찾을수 있다.
손으로 해보면 왜 그런지 쉽게 알 수 있다.
값을 추가 하는 공식은 만일 5번째에 값을 추가하게 되면, 그림상
5 , 5~6 , 1~8 이 5를 포함하므로
E[5], E[6], E[8] 에 값이 추가되어야 한다.
이는 합을 구할때와 반대로 맨 오른쪽 비트값만큼 더 해주면된다.
V배열의 크기가 넘지 않을때까지
아래는 값을 추가할때 와 합을 구하는 코드이다.
#define NSIZE 100
int tree[NSIZE];
void AddBIT(int idx, int val){
while (idx <= NSIZE){
tree[idx] += val;
idx += (idx&-idx);
}
}
void SumBIT(int idx){
int ret = 0;
while (idx){
ret += tree[idx];
idx -= (idx&-idx);
}
return ret;
}두 함수의 복잡도는 모두 O(logn) 이다.
