---

의사 결정 트리

무언가를 결정할 수 있는 기준들을 학습하는 모델

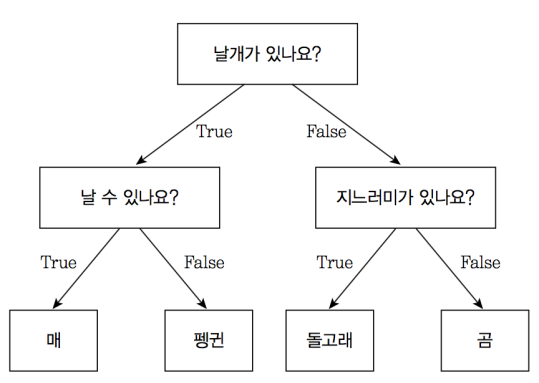
이미지 출처:https://tensorflow.blog

🌲 좋은 트리의 기준

1. DECISION TREE에서 마지막 노드인 leaf node에서 동일한 레이블의 데이터만 있을 때, 분류 정확도가 높다고 할 수 있다.
2. 트리의 깊이가 짧으면 모델의 학습 속도가 빠르다고 할 수 있다.
   (feature선택 순서에 따라 트리의 깊이가 달라지기도 한다.)

✔️ 트리 생성 전, 알아둘 것

1. root 노드는 모든 데이터를 고려한다.
2. 하위 노드로 내려갈수록 점점 데이터가 분류된다.

🔍 트리생성과정

1. 노드에 하나의 class만 있거나, 더 이상 고려할 feature가 없으면 leaf node 분류하고 자식노드를 생성하지 않는다.
   (feature가 없어서 leaf node가 된 경우, 더 많은 class를 결과 lable로 선택한다.)
2. 각 노드에서는 데이터를 잘 나눠주는 feature를 선택한다.
3. 선택된 feature에 대한 값마다 자식노드를 생성한다.
4. 1부터 생성과정을 반복한다.

Entropy

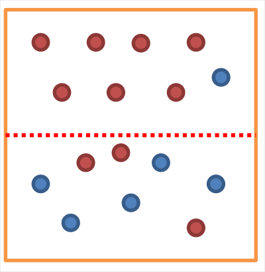
이미지 출처: https://ratsgo.github.io

• Purity : 한 쪽 데이터만 존재할수록, 더 깨끗하다.

• Entropy : 무질서도. Purity의 반대개념 (Impurity)

  A영역에 대해 K 범주에 속하는 데이터들의 entropy는 다음과 같이 계산된다.

  $Entropy(A)=-\sum_{k=1}^m p_klog_2(p_k)$

  (이때 Pk 는 A영역에 속하는 데이터들 중 K 범주에 속하는 데이터들의 비율이다.)

Entropy가 크다. = 분류가 잘 안 되었다. = 정보가 많다.

Entropy는 0에서 1사이의 값을 갖는다. 즉, 확률값을 의미한다고 할 수 있다.

Information Gain (IG)

부모노드의 엔트로피 – 자식노드의 엔트로피

Entropy가 작을수록 분류가 잘된 것이다.

즉, 부모 노드의 엔트로피에 비해 자식노드의 엔트로피가 작을수록 더 분류가 잘 되는 것을 의미한다.

따라서, 각 노드에서 분류할 feature선택할 때, IG의 값이 커지도록 feature를 선택한다. (ID3 알고리즘)

🖌 feature가 categorical feature가 아니라 real-value feature (상수)이라면 value bin 으로 나누어 범주화하여 트리를 만든다.

부가적인 내용들

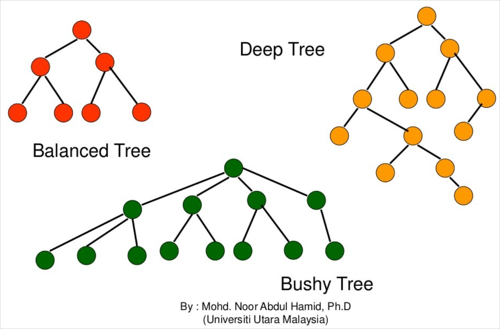
🔍 Tree 모양에 따른 용어들

• balanced tree: 이진트리

• deep tree: 깊은 모양

• bushy tree: 빗자루모양

• left skewed: 왼쪽으로만 가지가 쳐진 의사결정트리

• Right skewed: 오른쪽으로만 가지가 쳐진 의사결정트리

🖌 의사결정나무는 과적합되기 쉽다.

이유 1 : 뒤에 있는 자식노드에서 어떤 문제가 생길지 고려하지 않는 일종의 그리디 알고리즘이다.

이유 2 : 중간에서 feature을 하나 잘못 선택하면 뒤에서 너무 과적합이 되려는 경향이 있다.

🖌 의사결정나무는 normalizaion(정규화)할 필요가 없다.
정규화를 하여도 수치만 바뀔 뿐, 분류 기준은 바뀌지 않는다.

🖌 의사결정나무는 비선형문제인 XOR과 같은 문제를 해결하기 어렵다.