위키북스의 파이썬 머신러닝 완벽 가이드 책을 토대로 공부한 내용입니다.
1. ROC 곡선
ROC 곡선과 이에 기반한 AUC 스코어는 이진 분류의 예측 성능 측정에서 중요하게 사용되는 지표이다. ROC 곡선(Receiver Operation Characteristic Curve)는 일반적으로 의학 분야에서 많이 사용되지만, ML의 이진 분류 모델의 예측 성능을 판단하는 중요한 평가 지표이기도 하다. ROC 곡선은 FPR(Flase Positive Rate)가 변할 때 TPR(True Positive Rate)가 어떻게 변하는지를 나타내는 곡선이다. 여기서 TPR은 TP / (FN + TP)로 재현율을 의미하며 민감도라고도 불린다. 그리고 민감도에 대응하는 지표로는 TNR(True Negative Rate)이 있고, 특이성(Specificity)이라고 불린다.
- 민감도(TPR)는 실제값 Positive(양성)가 정확히 예측돼야 하는 수준을 나타낸다.
- 특이성(TNR)은 실제값 Negative(음성)가 정확히 예측돼야 하는 수준을 나타낸다.
TNR은 TN / (FP + TN)으로 구할 수 있고, FPR은 FP / (FP + TN)이므로 1-TNR 또는 1-특이성으로 표현된다.FPR = FP / (FP + TN) = 1 - 특이성
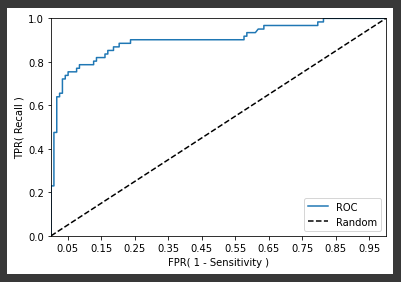
위 이미지는 ROC 곡선의 예이다. 가운데 직선은 ROC 곡선의 최저값이고, ROC 곡선이 가운데 직선에 가까울수록 성능이 떨어지는 것이며, 멀어질수록 성능이 뛰어난 것이다. ROC 곡선은 FPR을 0부터 1까지 변화시키면서 TPR의 변화값을 구한다. 그리고 FPR을 0부터 1까지 변화시키는 방법은 분류 결정 threshold를 변화시키면 된다. threshold는 Positive 예측값을 결정하는 확률의 기준이기 때문에 FPR을 0으로 만드려면 threshold는 1로 지정하면 된다. FPR은 FP / (FP + TN)이기 때문에 Positive로 예측하는 경우가 없도록 하면 FP가 0이 되어 FPR도 0이 된다. 그리고 FPR을 1로 만드려면 TN을 0으로 만들면 되기 때문에 Negative로 예측하는 경우가 없도록 threshold를 0으로 만들면 된다. 따라서 ROC 곡선은 threshold 값을 1부터 0까지 변화시키며 FPR을 구하고, FRP 값의 변화에 따른 TPR 값을 구하는 곡선이다.
사이킷런은 ROC 곡선을 구하기 위해 roc_curve() API를 제공한다.
- 입력 파라미터
- y_true : 실제 class 값 array (array shape=[데이터 건수])
- y_score : predict_proba()의 반환 값 array에서 Positive column의 예측 확률이 보통 사용됨. (array_shape=[n_samples])
- 반환 값
- fpr : fpr 값을 array로 반환
- tpr : tpr 값을 array로 반환
- thresholds : threshold 값 array
roc_curve() API를 이용해 타이타닉 생존자 예측 모델의 FPR, TPR, threshold를 구하고, ROC 곡선을 시각화해보았다.
from sklearn.metrics import roc_curve # 레이블 값이 1일때의 예측 확률을 추출 pred_proba_class1 = lr_clf.predict_proba(X_test)[:, 1] print('max predict_proba:', np.round(np.max(pred_proba_class1), 2)) fprs , tprs , thresholds = roc_curve(y_test, pred_proba_class1) print('thresholds[0](=max predict_proba+1):', np.round(thresholds[0], 2)) # 반환된 임곗값 배열에서 샘플로 데이터를 추출하되, 임곗값을 5 Step으로 추출. # thresholds[0]은 max(예측확률)+1로 임의 설정됨. 이를 제외하기 위해 np.arange는 1부터 시작 thr_index = np.arange(1, thresholds.shape[0], 5) print('샘플 추출을 위한 임곗값 배열의 index:', thr_index) print('샘플 index로 추출한 임곗값: ', np.round(thresholds[thr_index], 2)) # 5 step 단위로 추출된 임계값에 따른 FPR, TPR 값 print('샘플 임곗값별 FPR: ', np.round(fprs[thr_index], 3)) print('샘플 임곗값별 TPR: ', np.round(tprs[thr_index], 3))[output]
def roc_curve_plot(y_test , pred_proba_c1): # 임곗값에 따른 FPR, TPR 값을 반환 받음. fprs , tprs , thresholds = roc_curve(y_test ,pred_proba_c1) # ROC Curve를 plot 곡선으로 그림. plt.plot(fprs , tprs, label='ROC') # 가운데 대각선 직선을 그림. plt.plot([0, 1], [0, 1], 'k--', label='Random') # FPR X 축의 Scale을 0.1 단위로 변경, X,Y 축명 설정등 start, end = plt.xlim() plt.xticks(np.round(np.arange(start, end, 0.1),2)) plt.xlim(0,1) plt.ylim(0,1) plt.xlabel('FPR( 1 - Sensitivity )') plt.ylabel('TPR( Recall )') plt.legend() plt.show() roc_curve_plot(y_test, lr_clf.predict_proba(X_test)[:, 1] )[output]
2. AUC
일반적으로 ROC 곡선 자체는 FPR과 TPR의 변화값을 보는 데 이용하며 분류의 성능 지표로 사용되는 것은 ROC 곡선 면적에 기반한 AUC 값으로 결정된다. AUC(Area Under Curve) 값은 ROC 곡선 밑의 면적을 구한 것으로서 일반적으로 1에 가까울수록 좋은 수치이다. AUC 수치가 커지려면 FPR이 작은 상태에서 얼마나 큰 TPR을 얻을 수 있는지가 관건이다. 따라서 ROC 곡선이 가운데 직선에서 멀어지고 왼쪽 상단의 모서리 쪽으로 가까워져 직사각형에 가까운 곡선이 되어 면적이 1에 가까워지면 좋은 ROC AUC 성능을 얻게 된다. 사이킷런에서는 ROC AUC 값을 구하기 위해 roc_auc_score() API를 제공한다.
from sklearn.metrics import roc_auc_score ### 아래는 roc_auc_score()의 인자를 잘못 입력한 것으로, 책에서 수정이 필요한 부분입니다. ### 책에서는 roc_auc_score(y_test, pred)로 예측 타겟값을 입력하였으나 ### roc_auc_score(y_test, y_score)로 y_score는 predict_proba()로 호출된 예측 확률 ndarray중 Positive 열에 해당하는 ndarray입니다. #pred = lr_clf.predict(X_test) #roc_score = roc_auc_score(y_test, pred) pred_proba = lr_clf.predict_proba(X_test)[:, 1] roc_score = roc_auc_score(y_test, pred_proba) print('ROC AUC 값: {0:.4f}'.format(roc_score))[output]
마지막으로 이전에 만든 get_clf_eval() 함수에 ROC AUC 값까지 출력하도록 해준다.
def get_clf_eval(y_test, pred=None, pred_proba=None): confusion = confusion_matrix( y_test, pred) accuracy = accuracy_score(y_test , pred) precision = precision_score(y_test , pred) recall = recall_score(y_test , pred) f1 = f1_score(y_test,pred) # ROC-AUC 추가 roc_auc = roc_auc_score(y_test, pred_proba) print('오차 행렬') print(f'TN {confusion[0][0]}\t/ FP {confusion[0][1]}') print(f'FN {confusion[1][0]}\t/ TP {confusion[1][1]}') # ROC-AUC print 추가 print('정확도: {0:.4f}, 정밀도: {1:.4f}, 재현율: {2:.4f},\ F1: {3:.4f}, AUC:{4:.4f}'.format(accuracy, precision, recall, f1, roc_auc))