위키북스의 파이썬 머신러닝 완벽 가이드 책을 토대로 공부한 내용입니다.
1. 규제 선형 모델의 개요
회귀 모델은 적절하게 데이터에 적합하면서도 회귀 계수가 기하급수적으로 커지는 것을 제어할 수 있어야한다. 이전까지는 선형 모델의 비용 함수는 실제 값과 예측 값의 차이를 최소화하는 것만 고려하였다. 그러다보니 과적합이 발생하여 회귀 계수가 쉽게 커졌다. 이를 반영하여 비용 함수는 학습 데이터의 잔차 오류 값을 최소로 하는 방법과 과적합을 방지하기 위해 회귀 계수가 커지지 않도록 하는 방법이 서로 균형을 이뤄야 한다.따라서 회귀 계수의 크기를 제어하여 과적합을 개선하기 위해 비용 함수를 변경해야 한다.
비용 함수 목표 =
여기서 alpha는 학습 데이터 적합 정도와 회귀 계수 값의 크기 제어를 수행하는 튜닝 파라미터이다. alpha가 0이나 매우 작은 값이라면 비용 함수 식은 기존과 동일한 식으로 근사가 가능할 것이다. 반면에 alpha가 무한대에 가깝게 커진다면 비용 함수 식은 단순히 W값을 0으로 만드는 것이 Cost 함수의 목표가 될 것이다. 즉, alpha를 0에서부터 지속적으로 값을 증가시키면 회귀 계수 값의 크기를 감소시킬 수 있다. 이처럼 비용 함수에 alpha 값으로 패널티를 부여해 회귀 계수 값의 크기를 감소시켜 과적합을 개선하는 방식을 규제(Regularization)라고 부른다. 규제는 크게 L2 방식과 L1 방식으로 구분된다. L2 규제는 위와 같이 를 부여하는 하는 방식이며, L2 규제를 적용한 회귀를 릿지(Ridge) 회귀라고 한다. L1 규제는 를 부여하는 방식이고, L1 규제를 적용한 회귀는 라쏘(Lasso) 회귀라고 부른다. L1 규제를 적용하면 영향력이 크지 않은 회귀 계수를 0으로 만든다.
2. 릿지 회귀
사이킷런은 Ridge 클래스를 통해 릿지 회귀를 구현한다. Ridge 클래스의 주요 생성 파라미터는 alpha이며, 이는 릿지 회귀의 alpha L2 규제 계수이다. 보스턴 주택 가격 dataset을 사용하여 Ridge 클래스로 다시 예측해 보고 성능을 평가해 보겠다.
# 앞의 LinearRegression예제에서 분할한 feature 데이터 셋인 X_data과 Target 데이터 셋인 Y_target 데이터셋을 그대로 이용 import numpy as np import matplotlib.pyplot as plt import pandas as pd import seaborn as sns from scipy import stats from sklearn.datasets import load_boston from sklearn.linear_model import Ridge from sklearn.model_selection import cross_val_score %matplotlib inline # boston 데이타셋 로드 boston = load_boston() # boston 데이타셋 DataFrame 변환 bostonDF = pd.DataFrame(boston.data , columns = boston.feature_names) # boston dataset의 target array는 주택 가격임. 이를 PRICE 컬럼으로 DataFrame에 추가함. bostonDF['PRICE'] = boston.target print('Boston 데이타셋 크기 :',bostonDF.shape) y_target = bostonDF['PRICE'] X_data = bostonDF.drop(['PRICE'],axis=1,inplace=False) ridge = Ridge(alpha = 10) neg_mse_scores = cross_val_score(ridge, X_data, y_target, scoring="neg_mean_squared_error", cv = 5) rmse_scores = np.sqrt(-1 * neg_mse_scores) avg_rmse = np.mean(rmse_scores) print(' 5 folds 의 개별 Negative MSE scores: ', np.round(neg_mse_scores, 3)) print(' 5 folds 의 개별 RMSE scores : ', np.round(rmse_scores,3)) print(' 5 folds 의 평균 RMSE : {0:.3f} '.format(avg_rmse))[output]
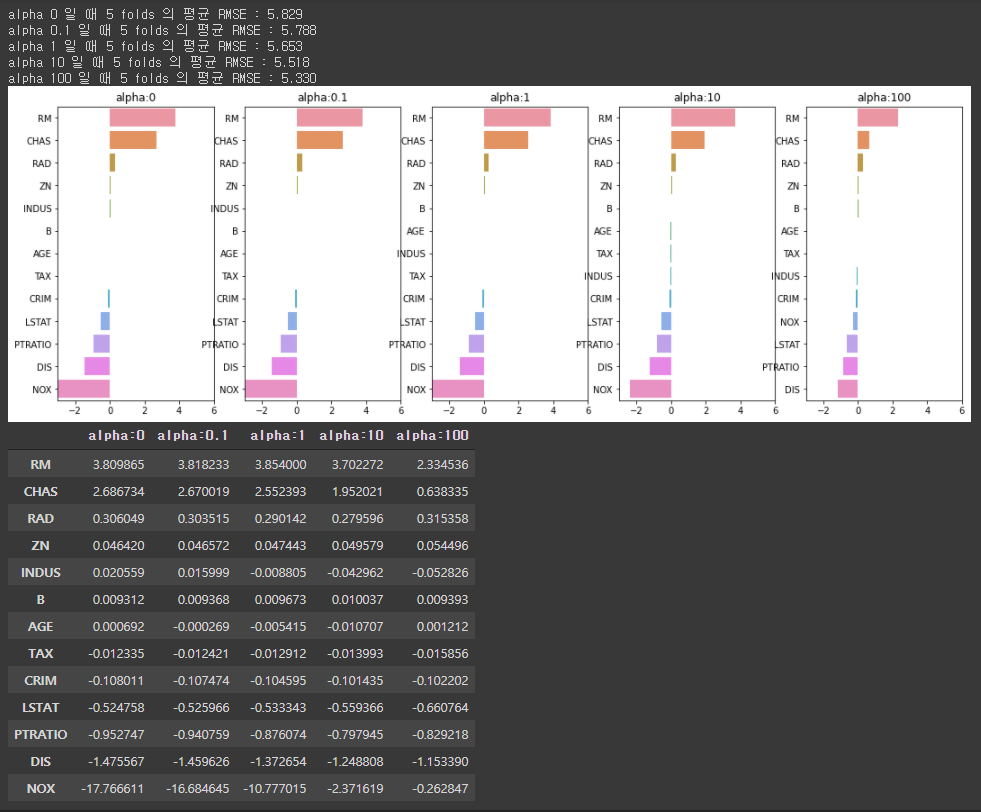
5개 fold의 평균 RMSE는 5.518로 LinearRegression의 평균 RMSE인 5.829보다 더 좋은 성능을 보인다. 다음은 alpha 값을 0~100 사이 값으로 변화를 주면서 RMSE와 회귀 계수값이 어떻게 변화하는지 알아보겠다.# Ridge에 사용될 alpha 파라미터의 값들을 정의 alphas = [0, 0.1, 1, 10, 100] # 각 alpha에 따른 회귀 계수 값을 시각화하기 위해 5개의 열로 된 맷플롯립 축 생성 fig, axs = plt.subplots(figsize=(18,6), nrows=1, ncols=5) # 각 alpha에 따른 회귀 계수 값을 데이터로 저장하기 위한 DataFrame 생성 coeff_df = pd.DataFrame() # alphas list 값을 iteration하면서 alpha에 따른 평균 rmse 구하고, 회귀 계수 값 시각화 및 데이터 저장. pos는 axis의 위치 지정 for pos, alpha in enumerate(alphas): ridge = Ridge(alpha = alpha) ridge.fit(X_data, y_target) #cross_val_score를 이용하여 5 fold의 평균 RMSE 계산 neg_mse_scores = cross_val_score(ridge, X_data, y_target, scoring="neg_mean_squared_error", cv = 5) avg_rmse = np.mean(np.sqrt(-1 * neg_mse_scores)) print('alpha {0} 일 때 5 folds 의 평균 RMSE : {1:.3f} '.format(alpha,avg_rmse)) # alpha에 따른 피처별 회귀 계수를 Series로 변환하고 이를 DataFrame의 컬럼으로 추가. coeff = pd.Series(data=ridge.coef_, index=X_data.columns ) colname='alpha:'+str(alpha) coeff_df[colname] = coeff # 막대 그래프로 각 alpha 값에서의 회귀 계수를 시각화. 회귀 계수값이 높은 순으로 표현 coeff = coeff.sort_values(ascending=False) axs[pos].set_title(colname) axs[pos].set_xlim(-3,6) sns.barplot(x=coeff.values, y=coeff.index, ax=axs[pos]) # for 문 바깥에서 맷플롯립의 show 호출 및 alpha에 따른 피처별 회귀 계수를 DataFrame으로 표시 plt.show() # alpha 값에 따른 컬럼별 회귀계수 출력 sort_column = 'alpha:'+str(alphas[0]) coeff_df.sort_values(by=sort_column, ascending=False)[output]
alpha 값을 계속 증가시킬수록 회귀 계수 값이 작아지는 것을 알 수 있다. 특히 NOX feature의 경우 굉장히 크게 작아지는 것을 볼 수 있다. 하지만 릿지 회귀의 경우에 회귀 계수를 0으로 만들지는 않는다.
3. 라쏘 회귀
w의 절대값에 패널티를 부여하는 L1 규제를 선형 회귀에 적용한 것이 라쏘(Lasso) 회귀이다. L2 규제가 회귀 계수의 크기를 감소시키는 데 반해, L1 규제는 불필요한 회귀 계수를 급격하게 감소시켜 0으로 만들고 제거한다. 이러한 측면에서 L1 규제는 적절한 feature만 회귀에 포함시키는 feature 선택의 특성을 가지고 있다.
사이킷런은 Lasso 클래스를 통해 라쏘 회귀를 구현하였다. Lasso 클래스의 주요 생성 파라미터는 alpha이며, 이는 L1 규제 계수이다. 이 Lasso 클래스를 이용하여 릿지 회귀와 유사하게 라쏘의 alpha 값을 변화시키면서 RMSE와 각 feature의 회귀 계수를 출력해보겠다.
from sklearn.linear_model import Lasso, ElasticNet # alpha값에 따른 회귀 모델의 폴드 평균 RMSE를 출력하고 회귀 계수값들을 DataFrame으로 반환 def get_linear_reg_eval(model_name, params=None, X_data_n=None, y_target_n=None, verbose=True, return_coeff=True): coeff_df = pd.DataFrame() if verbose : print('####### ', model_name , '#######') for param in params: if model_name =='Ridge': model = Ridge(alpha=param) elif model_name =='Lasso': model = Lasso(alpha=param) elif model_name =='ElasticNet': model = ElasticNet(alpha=param, l1_ratio=0.7) neg_mse_scores = cross_val_score(model, X_data_n, y_target_n, scoring="neg_mean_squared_error", cv = 5) avg_rmse = np.mean(np.sqrt(-1 * neg_mse_scores)) print('alpha {0}일 때 5 폴드 세트의 평균 RMSE: {1:.3f} '.format(param, avg_rmse)) # cross_val_score는 evaluation metric만 반환하므로 모델을 다시 학습하여 회귀 계수 추출 model.fit(X_data_n , y_target_n) if return_coeff: # alpha에 따른 피처별 회귀 계수를 Series로 변환하고 이를 DataFrame의 컬럼으로 추가. coeff = pd.Series(data=model.coef_ , index=X_data_n.columns ) colname='alpha:'+str(param) coeff_df[colname] = coeff return coeff_df # 라쏘에 사용될 alpha 파라미터의 값들을 정의하고 get_linear_reg_eval() 함수 호출 lasso_alphas = [ 0.07, 0.1, 0.5, 1, 3] coeff_lasso_df =get_linear_reg_eval('Lasso', params=lasso_alphas, X_data_n=X_data, y_target_n=y_target) # 반환된 coeff_lasso_df를 첫번째 컬럼순으로 내림차순 정렬하여 회귀계수 DataFrame출력 sort_column = 'alpha:'+str(lasso_alphas[0]) coeff_lasso_df.sort_values(by=sort_column, ascending=False)[output]
alpha 값이 증가함에 따라 일부 feature의 회귀 계수는 0으로 바뀌는 것을 볼 수 있다. 이렇게 회귀 계수가 0인 feature가 회귀 식에서 제외되면서 L1 규제를 이용하여 feature 선택의 효과를 얻을 수 있다.
4. 엘라스틱넷 회귀
엘라스틱넷(Elastic Net) 회귀는 L2 규제와 L1 규제를 결합한 회귀이다. 라쏘 회귀는 서로 상관관계가 높은 feature들 중에서 중요 feature 만을 셀렉션하고 다른 feature들은 모두 회귀 계수를 0으로 만드는 성향이 강하다. 특히 이러한 성향으로 인해 alpha 값에 따라 회귀 계수의 값이 급격히 변동할 수도 있다. 엘라스틱넷 회귀는 이러한 점을 완화하기 위해 L2 규제를 라쏘 회귀에 추가한 것이다. 반대로 엘라스틱넷 회귀의 단점은 L1과 L2 규제가 결합된 규제로 인해 수행시간이 상대적으로 오래 걸리는 것이다.
사이킷런은 ElasticNet 클래스를 통해 엘라스틱넷 회귀를 구현할 수 있고, 주요 생성 파라미터는 alpha와 l1_ratio이다. alpha는 Ridge와 Lasso 클래스의 alpha와는 다르다. 엘라스틱넷의 규제는 aL1 + bL2로 정의할 수 있는데 여기서 alpha는 a+b이다. 그리고 l1_ratio는 a/(a+b)이다. l1_ratio가 0이면 a가 0이 되므로 L2 규제과 같고, l1_ratio가 1이면 b가 0이므로 L1 규제와 같다.
# 엘라스틱넷에 사용될 alpha 파라미터의 값들을 정의하고 get_linear_reg_eval() 함수 호출 # l1_ratio는 0.7로 고정 elastic_alphas = [ 0.07, 0.1, 0.5, 1, 3] coeff_elastic_df =get_linear_reg_eval('ElasticNet', params=elastic_alphas, X_data_n=X_data, y_target_n=y_target) # 반환된 coeff_elastic_df를 첫번째 컬럼순으로 내림차순 정렬하여 회귀계수 DataFrame출력 sort_column = 'alpha:'+str(elastic_alphas[0]) coeff_elastic_df.sort_values(by=sort_column, ascending=False)[output]
l1_ratio는 0.7로 고정하고 alpha에 따라 어떻게 변화하는지 살펴보았다. alpha가 0.5일 때 RMSE가 5.468로 가장 좋은 예측 성능을 보이고, 이전의 라쏘보다는 상대적으로 0이 되는 값이 적다는 것을 알 수 있다.
5. 선형 회귀 모델을 위한 데이터 변환
선형 모델은 일반적으로 feature와 target 간에 선형의 관계에 있다고 가정하고, 최적으 선형 함수를 찾아내어 결과를 예측한다. 또한 선형 회귀 모델은 feature와 target의 분포가 정규 분포 형태인 경우를 매우 선호한다. 특히 target은 정규 분포 형태가 아닌 특정값의 분포가 치우친 왜곡(Skew)된 형태의 분포도일 경우 예측 성능에 부정적인 영향을 미칠 가능성이 높다. 따라서 선형 회귀 모델을 적용하기 전에 먼저 데이터에 대한 스케일링/정규화 작업을 수행하는 것이 일반적이다. 일반적으로 feature dataset과 target dataset의 스케일링/정규화 작업을 수행하는 방법은 조금 다르다.
- StandardScaler 클래스를 이용해 평균이 0, 분산이 1인 표준 정규 분포를 가진 dataset으로 변환하거나 MinMaxScaler 클래스를 이용해 최솟값이 0이고, 최대값이 1인 값으로 정규화를 수행한다.
- 스테일링/정규화를 수행한 dataset에 다시 다항 특성을 적용하여 변환하는 방법이다. 보통 1번 방법을 통해 예측 성능에 향상이 없을 경우 이와 같은 방법을 적용한다.
- 원래 값에 log 함수를 적용하면 보다 정규 분포에 가까운 형태로 값이 분포하게 된다. 이러한 변환을 로그 변환(Log Transformation)이라고 부른다. 로그 변환은 매우 유용한 변환이며, 실제로 선형 회귀에서는 앞에서 소개한 1,2번 방법보다 로그 변환이 훨씬 많이 사용되는 변환 방법이다. 왜냐하면 1번 방법의 경우 예측 성능 향상을 크게 기대하기 어려운 경우가 많으며 2번 방법의 경우 feature의 개수가 매우 많을 경우에는 다향 변환으로 생성되는 feature의 개수가 기하급수로 늘어나서 과적합의 이슈가 발생할 수 있기 때문이다.
target 값의 경우는 일반적으로 로그 변환을 사용한다. 결정 값을 정규 분포나 다른 정규값으로 변환하면 다시 원본 target 값으로 복원하기 어려울 수 있으며, 왜곡된 분포도 형태의 target 값을 로그 변환하여 예측 성능 향항이 된 경우가 많은 사례에서 검증되었기 때문이다.
위에서 언급한 정규 분포 변환, 최대/최소값 정규화, 로그 변환과, degree를 추가할 때, 추가하지 않을 때로 나누어서 RMSE 값을 살펴 보겠다. 그리고 Ridge 클래스를 사용하며 alpha 값에 따른 변화도 같이 보도록 하겠다.
from sklearn.preprocessing import StandardScaler, MinMaxScaler, PolynomialFeatures # method는 표준 정규 분포 변환(Standard), 최대값/최소값 정규화(MinMax), 로그변환(Log) 결정 # p_degree는 다향식 특성을 추가할 때 적용. p_degree는 2이상 부여하지 않음. def get_scaled_data(method='None', p_degree=None, input_data=None): if method == 'Standard': scaled_data = StandardScaler().fit_transform(input_data) elif method == 'MinMax': scaled_data = MinMaxScaler().fit_transform(input_data) elif method == 'Log': scaled_data = np.log1p(input_data) else: scaled_data = input_data if p_degree != None: scaled_data = PolynomialFeatures(degree=p_degree, include_bias=False).fit_transform(scaled_data) return scaled_data # Ridge의 alpha값을 다르게 적용하고 다양한 데이터 변환방법에 따른 RMSE 추출. alphas = [0.1, 1, 10, 100] #변환 방법은 모두 6개, 원본 그대로, 표준정규분포, 표준정규분포+다항식 특성 # 최대/최소 정규화, 최대/최소 정규화+다항식 특성, 로그변환 scale_methods=[(None, None), ('Standard', None), ('Standard', 2), ('MinMax', None), ('MinMax', 2), ('Log', None)] for scale_method in scale_methods: X_data_scaled = get_scaled_data(method=scale_method[0], p_degree=scale_method[1], input_data=X_data) print(X_data_scaled.shape, X_data.shape) print('\n## 변환 유형:{0}, Polynomial Degree:{1}'.format(scale_method[0], scale_method[1])) get_linear_reg_eval('Ridge', params=alphas, X_data_n=X_data_scaled, y_target_n=y_target, verbose=False, return_coeff=False)[output]
결과를 보면 표준 정규 분포와 최대/최소값 정규화로 feature dataset을 변경해도 성능의 개선이 없다. 2차 다항식으로 변환했을 경우 성능 개선이 있지만 다항식 변환은 feature의 개수가 많을 경우 적용하지 힘들고, 데이터가 많아지면 계산에 많은 시간이 소모된다. 반면에 로그 변환을 보면 모든 alpha 값에 대해 비교적 좋은 성능 향상이 있는 것을 알 수 있다.