위키북스의 파이썬 머신러닝 완벽 가이드 책을 토대로 공부한 내용입니다.
1. K-평균 알고리즘
K-평균은 군집화(Clustering)에서 가장 일반적으로 사용되는 알고리즘이다. K-평균은 군집 중심점(centroid)이라는 특정한 임의의 지점을 선택해 해당 중심에 가장 가까운 포인트들을 선택하는 군집화 기법이다. 군집 중심점은 선택된 포인트의 평균 지점으로 이동하고 이동된 중심점에서 다시 가까운 포인트를 선택, 다시 중심점을 평균 지점으로 이동하는 프로세스를 반복적으로 수행한다. 모든 데이터 포인트에서 더이상 중심점의 이동이 없을 경우에 반복을 멈추고 해당 중심점에 속하는 데이터 포인트들을 군집화하는 기법이다.
- K-평균
1. 먼저, 군집화의 기준이 되는 중심을 구성하려는 군집화 개수만큼 임의의 위치에 가져다 놓는다. 전체 데이터를 2개로 군집화하려면 2개의 중심을 임의의 위치에 가져다 놓는 것이다. 임의의 위치에 군집 중심점을 가져다 놓으면 반복적인 이동 수행을 너무 많이 해서 수행 시간이 오래 걸리기 때문에 초기화 알고리즘으로 적합한 위치에 중심점을 가져다 놓지만, 여기서는 설명을 위해 임의의 위치로 가정한다.
- 각 데이터는 가장 가까운 곳에 위치한 중심점에 소속된다.
- 이렇게 소속이 결정되면 군집 중심점을 소속된 데이터의 평균 중심으로 이동한다.
- 중심점이 이동했기 때문에 각 데이터는 기존에 속한 중심점보다 더 가까운 중심적이 있다면 해당 중심점으로 다시 소속을 변경한다.
- 다시 중심을 소속된 데이터의 평균 중심으로 이동한다.
- 중심점을 이동했는데 데이터의 중심점 소속 변경이 없으면 군집화를 종료한다. 그렇지 않다면 다시 4번 과정을 거쳐서 소속을 변경하고 이 과정을 반복한다.
- K-평균의 장점
- 일반적인 군집화에서 가장 많이 활용되는 알고리즘이다.
- 알고리즘이 쉽고 간결하다.
- K-평균의 단점
- 거리 기반 알고리즘으로 속성의 개수가 매우 많을 경우 군집화 정확도가 떨어진다. 이를 위해 PCA로 차원 감소를 적용해야 할 수도 있다.
- 반복을 수행하는데, 반복 횟수가 많을 경우 수행시간이 매우 느려진다.
- 몇 개의 군집(cluster)을 선택해야 할지 가이드하기가 어렵다.
2. 사이킷런 KMeans 클래스 소개
사이킷런의 KMeans 클래스는 여러 초기화 파라미터를 가지고 있고 그 중 중요한 파라미터를 살펴 보겠다. KMeans 초기화 파라미터 중 가장 중요한 파라미터는 nclusters이며, 이는 군집화할 개수, 즉 군집 중심점의 개수를 의미한다. init은 초기에 군집 중심점의 좌표를 설정할 방식을 말하며 보통은 임의로 중심을 설정하지 않고 일반적으로 k-means++ 방식으로 최초 설정한다. max_iter는 최대 반복 횟수이며, 이 횟수 이전에 모든 데이터의 중심점 이동이 없으면 종료한다. 그리고 KMeans는 fit과 fit_transform method를 이용해 수행된다. 이렇게 수행된 KMeans 객체는 군집화 수행이 완료돼 군집화와 관련된 주요 속성을 알 수가 있다. 주요 속성으로 먼저, labels 속성은 각 데이터 포인트가 속한 군집 중심정 label이고, clustercenters는 각 군집 중심점 좌표이다. 군집 중심점 좌표의 shape은 [군집 개수, 피쳐 개수]이며, 이를 이용하면 군집 중심점 좌표가 어디인지 시각화할 수 있다.
3. K-평균을 이용한 iris dataset 군집화
iris dataset을 이용하여 K-평균 군집화를 해보겠다. sepal length와 petal length에 따라 각 데이터의 군집화가 어떻게 결정되는지 확인해 보고, 분류 값과 비교해 보겠다. 3개 그룹으로 군집화하기 위해 n_cluster는 3, 초기 중심 설정 방식은 defalut 값인 k-means++, 최대 반복 횟수도 defalut 값인 max_iter=300으로 설정하여 KMeans 객체를 만들어 수행해보겠다.
from sklearn.preprocessing import scale from sklearn.datasets import load_iris from sklearn.cluster import KMeans import matplotlib.pyplot as plt import numpy as np import pandas as pd %matplotlib inline iris = load_iris() # 보다 편리한 데이터 Handling을 위해 DataFrame으로 변환 irisDF = pd.DataFrame(data=iris.data, columns=['sepal_length','sepal_width','petal_length','petal_width']) kmeans = KMeans(n_clusters=3, init='k-means++', max_iter=300,random_state=0) kmeans.fit(irisDF) print(kmeans.labels_)[output]
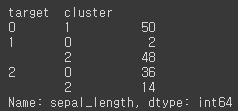
iris 데이터의 군집화 수행 결과는 kmeans 객체 변수로 반환 받은 뒤 keams의 label 속성값을 확인해 보았다. label의 값은 0, 1, 2로 첫 번째 군집, 두 번째 군집, 3번째 군집에 속하는 것을 의미한다. 이제 이제 실제 붓꽃 품종 분류 값과 얼마나 차이가 나는지로 군집화가 효과적으로 됬는지 확인해보겠다.irisDF['target'] = iris.target irisDF['cluster']=kmeans.labels_ iris_result = irisDF.groupby(['target','cluster'])['sepal_length'].count() print(iris_result)[output]
target 0인 데이터는 모두 1번 군집으로 잘 grouping 되었고 target 1인 데이터도 2개의 데이터만 제외하고 모두 0번 군집으로 grouping 되었지만 target 2인 데이터는 0번 군집과 2번 군집으로 분산되어 grouping 되었다.이번엔 군집화를 시각화해보도록 하겠다. 2차원 평면에 시각적으로 표현하기 위해 PCA를 이용하여 4개의 속성을 2개로 차원 축소한 뒤 데이터를 표현하도록 하겠다.
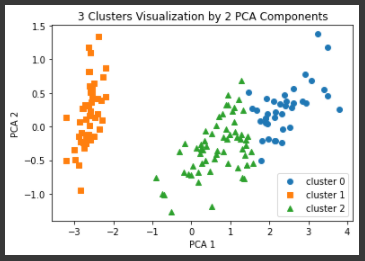
from sklearn.decomposition import PCA pca = PCA(n_components=2) pca_transformed = pca.fit_transform(iris.data) irisDF['pca_x'] = pca_transformed[:,0] irisDF['pca_y'] = pca_transformed[:,1] # cluster 값이 0, 1, 2 인 경우마다 별도의 Index로 추출 marker0_ind = irisDF[irisDF['cluster']==0].index marker1_ind = irisDF[irisDF['cluster']==1].index marker2_ind = irisDF[irisDF['cluster']==2].index # cluster값 0, 1, 2에 해당하는 Index로 각 cluster 레벨의 pca_x, pca_y 값 추출. o, s, ^ 로 marker 표시 plt.scatter(x=irisDF.loc[marker0_ind,'pca_x'], y=irisDF.loc[marker0_ind,'pca_y'], marker='o') plt.scatter(x=irisDF.loc[marker1_ind,'pca_x'], y=irisDF.loc[marker1_ind,'pca_y'], marker='s') plt.scatter(x=irisDF.loc[marker2_ind,'pca_x'], y=irisDF.loc[marker2_ind,'pca_y'], marker='^') plt.xlabel('PCA 1') plt.ylabel('PCA 2') plt.title('3 Clusters Visualization by 2 PCA Components') plt.legend(('cluster 0', 'cluster 1', 'cluster 2')) plt.show()[output]
cluster 1은 명확하게 다른 군집과 분리가 되어 있다. cluster 0과 cluster 2도 상당 수준 잘 분리되어 있지만 명확하게 분리가 되어 있진 않다.
4. 군집화 알고리즘 테스트를 위한 데이터 생성
사이킷런은 다양한 유형의 군집화 알고리즘을 테스트해 보기 위한 간단한 데이터 생성기를 제공한다. 대표적인 군집화용 데이터 생성기로는 make_blobs()와 make_classification() API가 있고, 이 외에 make_circle(), make_moon API 등 중심 기반의 군집화로 해결하기 어려운 dataset을 만드는 데 사용된다.
make_blobs()를 호출하면 feature dataset과 target dataset가 반환된다.
- make_blobs()의 파라미터
- n_samples : 생성할 총 데이터의 개수이다. default는 100개이다.
- n_features : 데이터의 feature 개수이다. 시각화를 목표로 할 경우 2개로 설정해 보통 첫 번째 feature는 x 좌표, 두 번째 feature는 y 좌표상에 표현한다.
- centers : int 값, 예를 들어 3으로 설정하면 군집의 개수를 나타내고, ndarray 형태로 표현할 경우 개별 군집 중짐점의 좌표를 의미한다.
- cluster_std : 생성될 군집 데이터의 표준 편차를 의미한다. 만일 float 값 0.8과 같은 형태로 지정하면 군집 내에서 데이터가 표준 편차 0.8을 가진 값으로 만들어진다. [0.8, 1.2, 0.6]과 같은 형태로 표현되면 3개의 군집에서 첫 번째 군집 내 데이터의 표준편차는 0.8, 두번째 군집 내 데이터의 표준 편차는 1.2, 세번째 군집 내 데이터의 표준 편차는 0.6으로 만들어진다. 군집별로 서로 다른 표준 편차를 가진 dataset을 만들 때 사용된다.
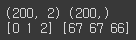
import numpy as np import matplotlib.pyplot as plt from sklearn.cluster import KMeans from sklearn.datasets import make_blobs %matplotlib inline X, y = make_blobs(n_samples=200, n_features=2, centers=3, cluster_std=0.8, random_state=0) print(X.shape, y.shape) # y target 값의 분포를 확인 unique, counts = np.unique(y, return_counts=True) print(unique,counts)[output]
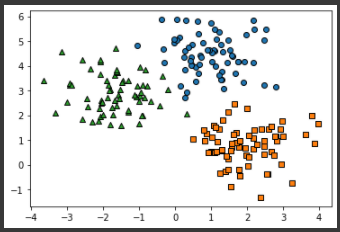
feature dataset X는 200개의 record와 2개의 feature를 가지므로 shape이 (200, 2)이고 target dataset y는 (200)이 된다. 그리고 3개의 cluster의 값은 0, 1, 2이며, 각각 67개, 67개, 66개로 균일하게 구성되어 있다. 이제 make_blob()으로 만든 feature dataset이 어떠한 군집화 분포를 가지고 만들어졌는지 확인해보겠다.import pandas as pd clusterDF = pd.DataFrame(data=X, columns=['ftr1', 'ftr2']) clusterDF['target'] = y target_list = np.unique(y) # 각 target별 scatter plot 의 marker 값들. markers=['o', 's', '^', 'P','D','H','x'] # 3개의 cluster 영역으로 구분한 데이터 셋을 생성했으므로 target_list는 [0,1,2] # target==0, target==1, target==2 로 scatter plot을 marker별로 생성. for target in target_list: target_cluster = clusterDF[clusterDF['target']==target] plt.scatter(x=target_cluster['ftr1'], y=target_cluster['ftr2'], edgecolor='k', marker=markers[target] ) plt.show()[output]
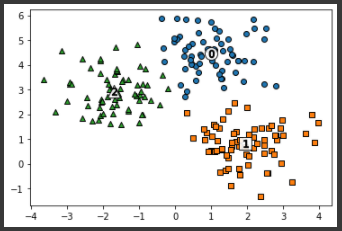
이번엔 생성한 dataset에 KMeans 군집화를 수행한 뒤 시각화를 해보겠다.# KMeans 객체를 이용하여 X 데이터를 K-Means 클러스터링 수행 kmeans = KMeans(n_clusters=3, init='k-means++', max_iter=200, random_state=0) cluster_labels = kmeans.fit_predict(X) clusterDF['kmeans_label'] = cluster_labels #cluster_centers_ 는 개별 클러스터의 중심 위치 좌표 시각화를 위해 추출 centers = kmeans.cluster_centers_ unique_labels = np.unique(cluster_labels) markers=['o', 's', '^', 'P','D','H','x'] # 군집된 label 유형별로 iteration 하면서 marker 별로 scatter plot 수행. for label in unique_labels: label_cluster = clusterDF[clusterDF['kmeans_label']==label] center_x_y = centers[label] plt.scatter(x=label_cluster['ftr1'], y=label_cluster['ftr2'], edgecolor='k', marker=markers[label] ) # 군집별 중심 위치 좌표 시각화 plt.scatter(x=center_x_y[0], y=center_x_y[1], s=200, color='white', alpha=0.9, edgecolor='k', marker=markers[label]) plt.scatter(x=center_x_y[0], y=center_x_y[1], s=70, color='k', edgecolor='k', marker='$%d$' % label) plt.show()[output]
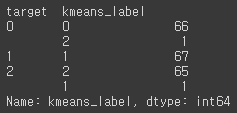
target 번호와 군집 번호는 서로 다른 값으로 나타나질 수 있다.print(clusterDF.groupby('target')['kmeans_label'].value_counts())[output]
각각의 target 들이 각각의 cluster로 잘 매핑되었다.make_blobs()는 cluster_std 파라미터로 데이터의 분포도를 조절한다. cluster_std가 작을수록 군집 중심에 데이터가 모여 있으며, 클수록 데이터가 퍼져 있게 된다.