한 줄 요약
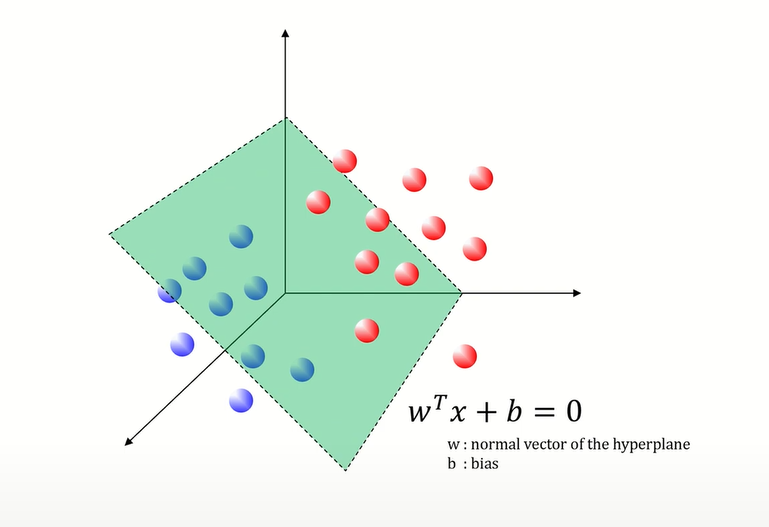
Support Vector Machine(SVM) 은 두 클래스 간의 간격(margin)을 최대화하는 결정 경계(hyper plane)을 찾기 위한 모델이며, 이때 이 hyper plane과 가장 가까운 데이터 포인트들을 서포트 벡터로 사용해 마진을 계산함.
- 두 클래스 간의 최대 간격(margin)을 찾는 것을 목표로 하며, 이 최대 간격을 가지는 하이퍼 플레인을 찾아내는 방식으로 동작함 (분류를 위한 기준 선을 정의하는 모델)
SVM 기본 원리
결정 경계(Decision Boundary, Hyper Plane)
데이터 포인트를 두 개의 클래스 중 하나로 분류하기 위한 기준 선(또는 평면)을 정의함
→ 이진 분류 뿐만 아니라 다중 클래스 분류 문제도 해결 가능
마진(Margin)
하이퍼 플레인과 각 클래스의 가장 가까운 데이터 포인트들(서포트 벡터들) 사이의 거리를 의미함 (plus plane과 minus plane 사이의 거리)
→ SVM의 목표는 이 마진을 maximize하는 것!
→ 마진이 클수록(소프트 마진) 일반화 성능이 좋아짐
서포트 벡터(Support Vectors)
마진 경계에 위치한 데이터 포인트들을 서포트 벡터라고 지칭하며, 서포트 벡터들은 하이퍼 플레인을 정의하는 데 중요한 역할을 함
→ SVM은 하이퍼 플레인을 정의할 때 전체 데이터셋을 사용하지 않고, 오직 서포트 벡터만 사용해 정의함
→ 따라서 비교적 적은 데이터로도 효율적으로 분류할 수 있게 되는 것!
SVM 기본 원리
오류를 감안해서 분류할 것인지, 최적의 마진을 목표로 할 것 인지에 대한 사전 정의가 필요함
→ 이에 따라서 두 가지 방법으로 SVM을 최적화 가능
Ⅰ. 마진 최대화
- 오류 일부 발생 감안
- 새로운 데이터에 대해서는 마진이 넓어 잘 분류될 가능성이 높음
Ⅱ. 오류 최소화
- 오류를 허용하지 않음
- 새로운 데이터에 대해서는 마진이 좁아 분류가 잘못될 가능성이 있음
SVM 주요 파라미터
, : 하이퍼 플레인을 결정하는 SVM 파라미터
- - 하이퍼 플레인의 방향을 결정
- - 하이퍼 플레인의 위치를 결정
: 모델 복잡도와 오류 허용 정도를 조절하는 SVM 하이퍼 파라미터 (오류를 얼마나 허용할 것인가를 결정하는 규제항)
- 최적화 문제를 라그랑지안 형태로 변환할 때, C는 슬랙 변수의 합을 제어해, 마진과 분류 오류 사이 균형을 맞추는 역할을 함
- 즉, 하이퍼 플레인의 마진 최대화를 목표로 할 때, 오류를 감안할 것인가 아니면 최소화할 것인가를 C가 조절함 (by 교차검증, 그리드 서치)
- C가 클수록 오류 최소화(마진이 줄어듦 = hard margin)
- C가 작을수록 마진 최대화(마진이 넓어짐 = soft margin)
: 하이퍼 플레인을 얼마나 유연하게 그릴지를 결정하는 하이퍼 파라미터 (클수록 오버피팅 발생 가능성 증가)
Linear과 Non-linear
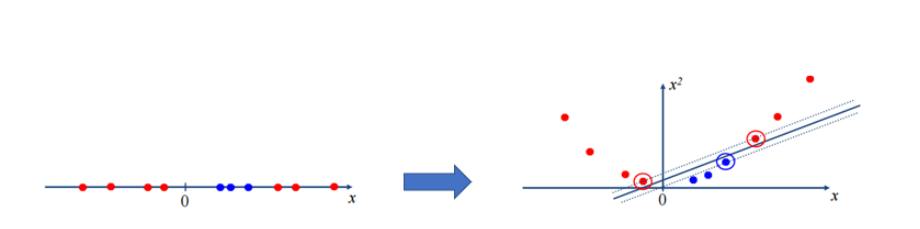
기본적으로 SVM은 선형 결정 경계를 찾아내지지만, 커널 함수를 사용함으로써 비선형 결정 경계를 정의할 수 있음
커널 함수를 통해 데이터 차원을 한 차원 더 늘리거나 데이터 자체를 변환하는 것처럼 다루어(커널 트릭), 선형적으로 구분되지 않는 데이터를 선형적으로 구분할 수 있게 만듦
- 커널 함수 - 데이터를 고차원으로 매핑하기 위해 사용하는 함수
- 일반적으로 시그모이드 커널, 다항 커널, RBF(Radial Basis Function) 커널 등을 이용함
- 그러나 주어진 데이터에 어떤 커널이 적합한지 명확하게 알기 어려움
- 만약 선택한 커널 함수가 데이터셋에 적합하지 않다면 모델 성능 저하 가능성 O
SVM의 장단점
장점
- 오버피팅 가능성 줄어듦
- 저차원, 고차원 공간의 적은 데이터에 대해서 분류 성능 좋음
- 데이터 포인트 수보다 피처 수가 더 많아도 성능 좋음
- 일반화 능력 ( 새로운 데이터에 대해서도 잘 작동 ) 이 우수함
- 데이터 피처 수가 적어도 성능 좋음
- 잡음(variance)에 강함
- SVM은 최적의 결정 경계를 찾는 것이 목표이다. 따라서, 다른 분류 알고리즘보다 더 높은 분류 성능을 보인다.
- 커널트릭을 사용하여 비선형 문제 또한 해결할 수 있음
단점
- 파라미터(C)가 작으면 마진 값이 커져 모델의 성능은 향상되지만 바운더리와 가까운 실제 대상 구분에 있어 틀릴 가능성이 있다.
- 커널함수 선택이 명확하지 않음
- 주어진 데이터에 어떤 커널이 적합한지 명확하게 알기 어려움
- 만약, 선택한 커널함수가 적합하지 않다면, SVM의 성능이 낮아짐
- 커널 함수 - 데이터를 고차원으로 매핑하기 위해 사용하는 함수. 일반적으로 선형 커널, 다항 커널, RBF(Radial Basis Function) 커널 등을 이용함
- 계산량 부담 있음
- 모든 데이터 포인트 쌍에 대해 계산을 수행해야 함
- 큰 데이터 셋에서는 학습 속도가 느릴 수 있음
- 데이터 피처 스케일링에 민감함
- 각 피처의 범위가 다르면 모델 성능 저하 가능성 up (표준화, 정규화 전처리 작업 필수)
- 거리 기반 모델이므로 데이터 포인트 간 거리 계산해야 해서 스케일링에 민감
- RBF 커널 함수를 사용하면 잘못된 가중치가 계산될 수 있음 (각 데이터 포인트 간 거리에 따라 가중치를 부여하는 것이므로)
- 데이터 스케일링이 다르면 하이퍼 파라미터 최적화가 어려워짐 (C, γ)
- 특성이 많을 때, 성능 저하 가능성이 높음
