선형대수의 여러가지 간단한 기법들을 파이썬 코드로 표현하는 방법을 배웠다. 1학년때 날 괴롭혔던 선형대수,,, 오랜만 ^.^,,,,
zip을 사용하여 vector 계산하기
[22]+[23]+[35] = [710]
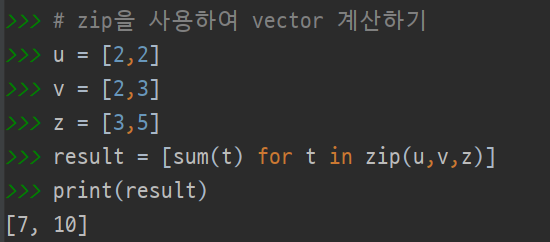
Scalar - Vector product
2([123]+[456])=2[579]=[101418]
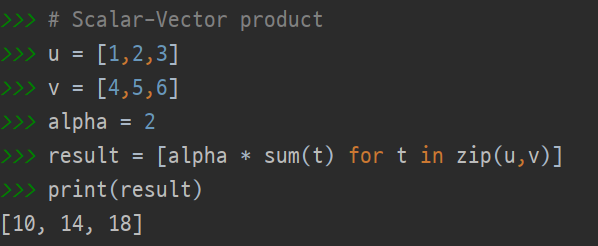
Matrix addition
[3645]+[5867]=[8141012]
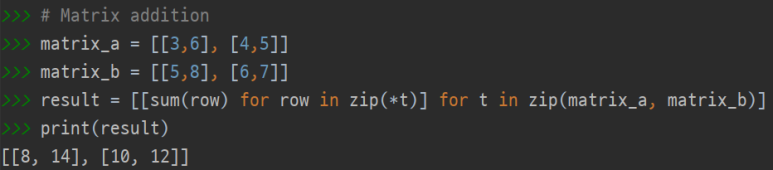
Scalar - Matrix Product
4 × [3465] = [12162420]
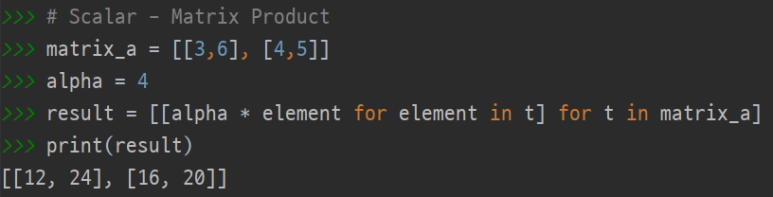
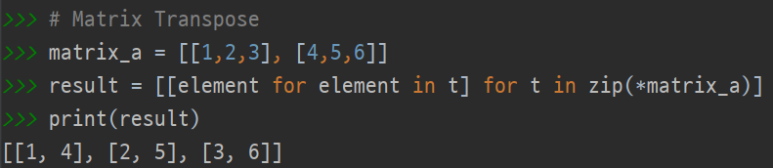
Matrix Transpose
A = [142536] , AT = ⎣⎢⎡123456⎦⎥⎤
Matrix Product
[121121]×⎣⎢⎡121113⎦⎥⎤=[5586]














