Linear Regression :: Gradient Descent

x^2의 최적값 찾기

import numpy as np
import matplotlib.pyplot as plt

x = np.arange(-10, 10, 1)
f_x = x ** 2

plt.plot(x, f_x)
plt.show()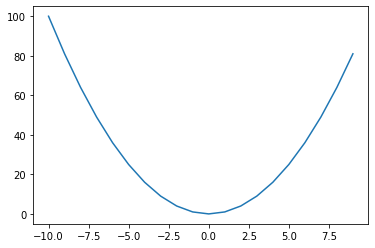

x_new = 10
derivative = []
y = []
learng_rate = 0.1
for i in range(100):
    old_value = x_new
    derivative.append(old_value - learng_rate * 2 * old_value)
    x_new = old_value - learng_rate * 2 * old_value
    y.append(x_new ** 2)

정해야 하는 것

learning rate에 대한 선정

얼마나 많이 loop을 돌 것인가?

1. 너무 작을 경우 : 끝까지 못감 & 시간이 오래걸림
2. 너무 클 경우 : 데이터가 튀는 문제 & 수렴하지 못하는 경우가 생김

plt.plot(x, f_x)
plt.scatter(derivative, y)
plt.show()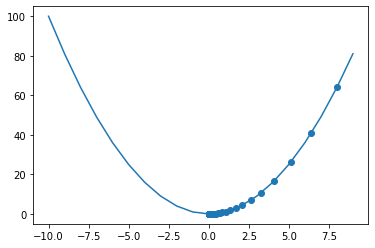

---

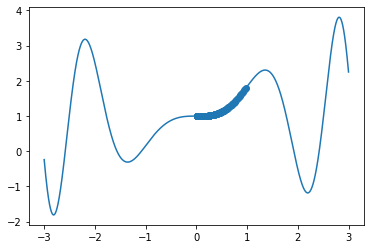
굴곡이 많은 함수의 경우

시작점에 따라 다른 최적값을 찾는다

def sin_function(x):
    return x * np.sin(x ** 2) + 1

def derivitive_f(x):
    return np.sin(x**2) + 2 * (x **2) * np.cos(x ** 2)

x = np.arange(-3, 3, 0.001)
f_x = sin_function(x)

plt.plot(x, f_x)
plt.show()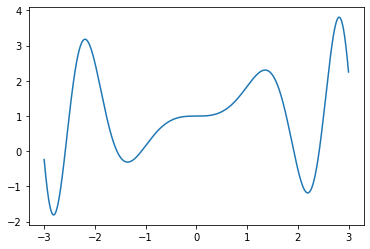

derivitive_f(3)

-15.988226228682427

x_new = 1
derivative = []
y = []
learng_rate= 0.01
for i in range(10000):
    old_value = x_new
    x_new = old_value - learng_rate * derivitive_f(old_value)
    derivative.append(x_new)
    y.append(sin_function(x_new))

plt.plot(x, f_x)
plt.scatter(derivative, y)
plt.show()

---

https://www.boostcourse.org/ai222/lecture/24512