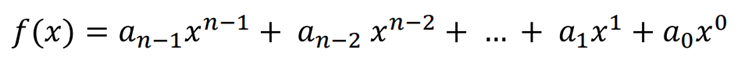GF(2^n)체
- 암호학에서 필요로 하는 연산 -> 덧셈, 뺄셈, 곱셈, 나눗셈
- 따라서 암호학에서는 체를 사용함
- 컴퓨터에서의 연산 시 양의 정수는 컴퓨터에 n-비트의 워드로 저장됨
- 따라서 정수의 범위는 0 ~ 2^n - 1 -> 모듈러 2^n 연산이 필요함
두 가지 사용 가능한 체
1. GF(p)
- 2^n보다 작은 가장 큰 소수 p를 이용해 Zp에 정의된 GF(p)를 사용함
- 그러나 이 방법을 적용하면, p로부터 2^n - 1사이의 정수들을 사용할 수 없기 때문에 비효율적임
- 예) 만약 n = 4면 2^4 = 16보다 작은 가장 큰 소수는 13
- 이 경우, 정수 13, 14, 15를 사용할 수 없음
- 만약 n = 8이면, 2^8 = 256이고, 이보다 작은 가장 큰 소수는 251
- 따라서 251, 252, 253, 254, 255는 사용할 수 없음
- 예) 만약 n = 4면 2^4 = 16보다 작은 가장 큰 소수는 13
2. GF(2^n)
- 원소의 개수가 2^n인 GF(2^n)체를 사용할 수 있음
- 이 집합의 원소들은 n 비트 워드임
- 예) n = 3일 때 n비트 워드 집합
- {000, 001, 010, 011, 100, 101, 110, 111}
- 그러나 상기의 비트로 구성된 각 원소들은 0부터 7까지의 정수로 생각하지 않고, n-비트 워드의 집합과 체에 대한 성질을 만족하는 두 개의 새로운 연산(덧셈, 곱셈)을 정의하여 사용함
- 예) n = 3일 때 n비트 워드 집합
다항식
- n-비트 워드 위에서 GF(2^n)의 모든 성질들을 만족하는 덧셈과 곱셈 연산에 대한 규칙을 직접 정의할 수 있음
- 하지만 n-비트의 워드를 차수 n-1의 다항식 형태로 생각하는 것이 훨씬 간단함
- 차수 n-1의 다항식:
- n-비트 워드를 다항식으로 표현하기 위한 규칙
- x의 지수승은 n-비트 워드에서 비트들의 위치를 정의함
- 이것은 가장 오른쪽에 있는 비트를 0의 위치에 놓고(x^0과 관련) 가장 왼쪽에 있는 비트를 n-1의 위치에 놓음(x^n-1과 관련)
- 항의 계수는 비트의 값을 나타냄
- 단, 비트는 0과 1의 값을 갖기 때문에 다항식의 계수는 0 또는 1임
다항식 예제) 다항식을 사용해서 8비트 워드 (10011001)을 표현하라
다항식의 연산
- 다항식의 관한 연산은 두 개의 연산을 포함함
- 계수에 관한 연산 및 두 개의 다항식에 관한 연산
- n-비트 워드를 표현하는 다항식들은 계수에 대한 체와 다항식에 대한 체를 가짐
- 계수에 대한 체: 0과 1의 값을 가지므로 GF(2)체를 사용
- 다항식에 대한 체: GF(2^n)체를 사용함
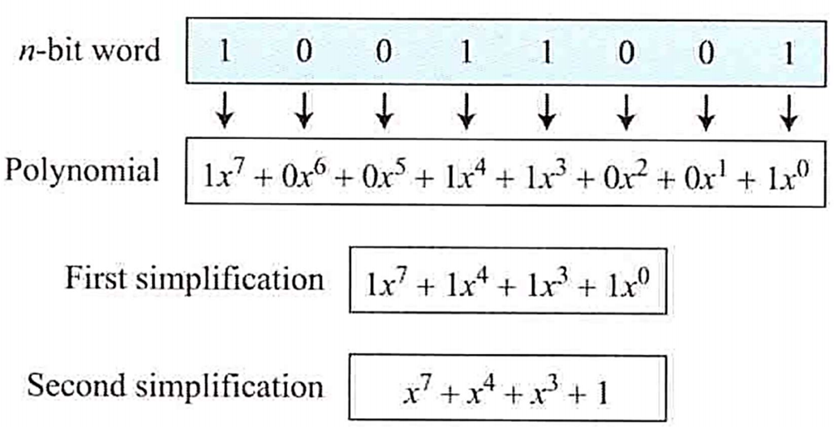
다항식의 연산 - 모듈러 다항식
- 두 다항식의 덧셈은 그 집합에 속하지 않는 다항식을 생성하지 않음
- 그러나 두 다항식의 곱셈은 n-1보다 큰 차수를 갖는 다항식을 생성할 수 있음
- GF(2^n)의 다항식의 집합에 대해서, 차수 n의 다항식의 군은 모듈러로 정의됨
- 이 경우 모듈러는 소수 다항식으로 동작하는데 이는 n보다 낮은 차수의 다항식으로 인수분해 될 수 없음을 의미함
- 기약 다항식 (Irreducible polynomial)이라 함
- 각 차수에 대해 기약 다항식이 하나 이상 존재하기 때문에 GF(2^n)을 정의할 때 모듈러로서 사용할 기약 다항식을 어떤 것으로 할 것인지 반드시 정해야 함
다항식의 연산 - 덧셈
- GF(2)에서 계수를 갖는 다항식에 대한 덧셈 연산
- GF(2)에 대응하는 항의 계수를 더함
- 차수가 n-1인 두 다항식의 합은 항상 차수 n-1의 다항식을 생성함
- 따라서 덧셈을 한 결과에 모듈러를 사용해 다항식의 차수를 줄일 필요가 없음
다항식의 연산 - 덧셈 예제1)

다항식의 연산 - 덧셈 예제2)

덧셈에 대한 항등원
- 다항식은 자신을 더하는 것은 0의 다항식을 만들기 때문에 다항식의 덧셈에 대한 항등원은 0의 다항식임
- 모든 계수가 0인 다항식
덧셈에 대한 역원
- GF(2)에서 계수를 가지는 다항식의 덧셈에 대한 역원은 바로 그 자신
- 즉 뺄셈 연산은 덧셈 연산과 같음을 의미함
다항식의 연산 - 곱셈
- 다항식의 곱셈은 첫 번째 다항식의 각 항과 두 번째 다항식의 각 항의 곱셈의 합임
- 곱셈에 대해서는 다음의 세 가지 사실이 중요함
- 계수의 곱셈은 GF(2)에서 이루어짐
- x^i, x^j를 곱한 결과는 x^(i+j)
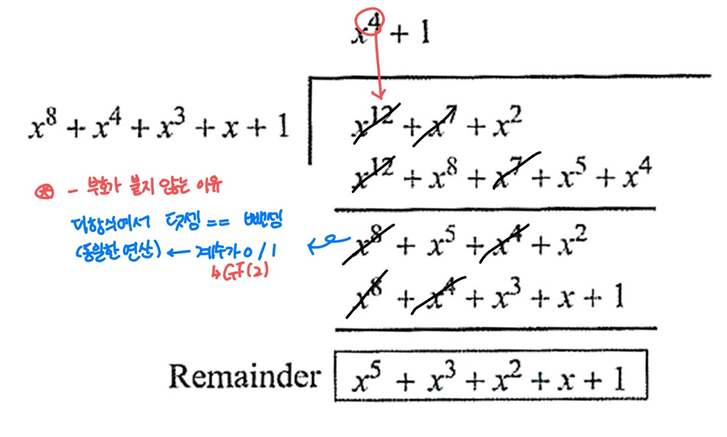
- 곱셈은 n-1보다 큰 차수를 가지는 항을 생성할 수도 있음
- 따라서 모듈러 다항식을 사용하여 곱셈한 결과를 줄일 필요가 있음
다항식의 연산 - 곱셈 예제

곱셈에 대한 항등원
- 항상 1임
- 예) GF(2^8)에서 곱셈에 대한 항등원은 00000001의 비트 형태
곱셈에 대한 역원
- 확장 유클리드 알고리즘을 사용해 계산 -> t1이 역원이 됨
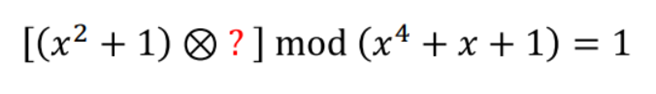
요약
-
유한 체 GF(2^n)은 n-비트 워드에 대한 덧셈, 뺄셈, 곱셈, 나눗셈 연산을 정의하기 위해 사용될 수 있으며 이 때 0에 의한 나눗셈은 제외함
-
각 n-비트 워드는 GF(2)에서 계수를 갖는 차수 n-1의 다항식으로서 표현되며, n-비트 워드에 대한 연산은 이 다항식의 연산과 같음을 의미함

-
모듈러 연산을 정의하기 위해서, 두 개의 다항식을 곱할 때 차수 n의 기약 다항식을 정할 필요가 있음
-
확장 유클리드 알고리즘은 곱셈 역원을 구하기 위해 다항식에 적용될 수 있음