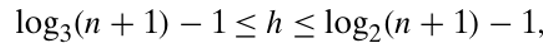Instance Simplification - Presorting
- 목록을 정렬하면 관련된 많은 문제가 쉬워짐
- 검색
- 중위수 계산
- 중복 (단일성) 검사
Element Uniqueness with Presorting
Brute force algorithm: 모든 요소의 쌍을 비교함
- O(n^2)
Presorting-based algorithm
- 효율적인 정렬 알고리즘별 정렬 (예를 들면 병합정렬)
- 배열을 스캔하여 인접 요소 쌍을 확인함
- Θ(nlogn) + O(n) = Θ(nlogn)
Gaussian Elimination
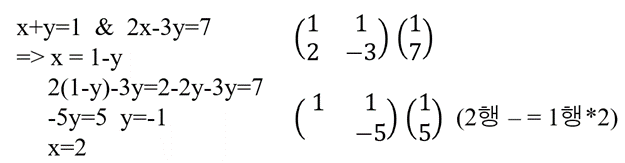
- Transform: 방정식 -> 행렬

- Θ(n^3)

- 문제점
- A[i, i] = 0 인 경우에 처리 불가
- A[i, i]가 매우 작은 값인 경우
- A[j, i]/A[i, i]가 반복 계산

temp = A[j, i] / A[i, i]
Representation Change: BST
- linear 대신 tree 표현 사용
- 이진 컴색 트리 속성을 사용해 이진 트리의 키 배열
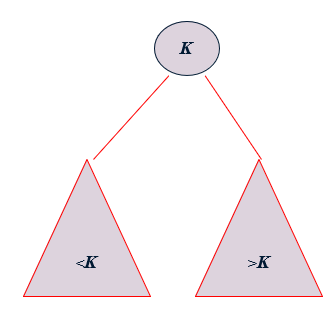
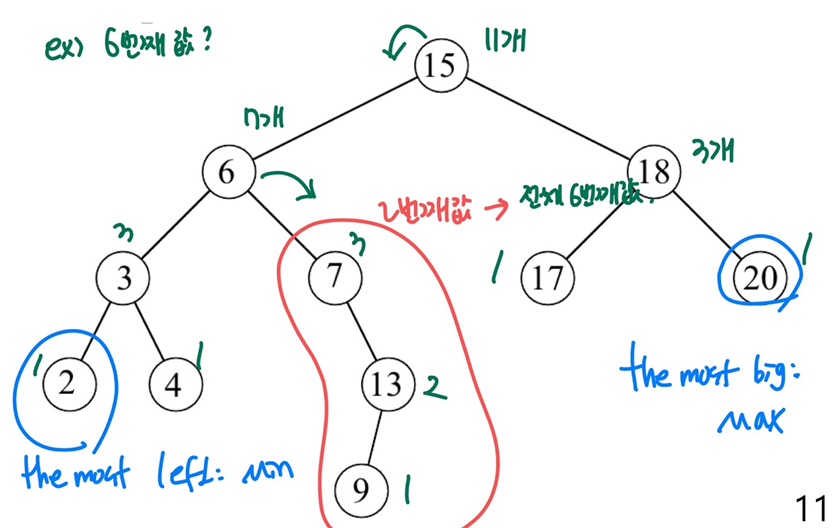
이진탐색트리 특징
- 노드의 왼쪽 하위 트리에는 노드의 키보다 작은 키가있는 노드만 포함됩니다.
- 노드의 오른쪽 하위 트리에는 노드의 키보다 큰 키가있는 노드만 포함됩니다.
- 왼쪽 및 오른쪽 하위 트리도 각각 이진 검색 트리 여야합니다.
- 중복된 키를 허용하지 않습니다.
Inorder tree walk (중위순회)
- 왼쪽 서브트리를 중위순회한다.
- 노드를 방문한다.
- 오른쪽 서브트리를 중위순회한다.

A B D F H K
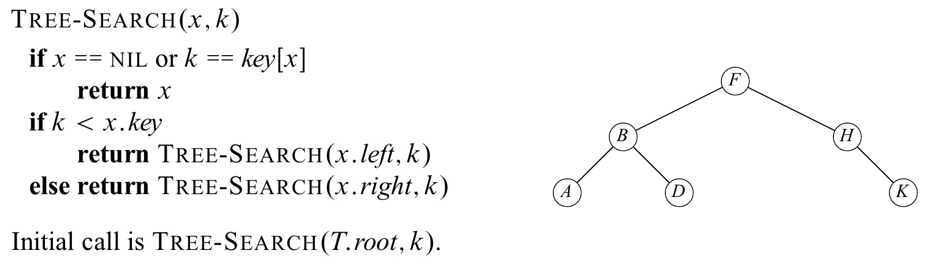
Search
- 루트에서 시작합니다.
- 검색 값을 루트와 비교해서 루트보다 작으면 왼쪽에 대해 재귀하고 크다면 오른쪽으로 재귀합니다.
- 일치하는 값을 찾을 때까지 절차를 반복합니다.
- 검색 값이 없으면 null을 반환합니다.
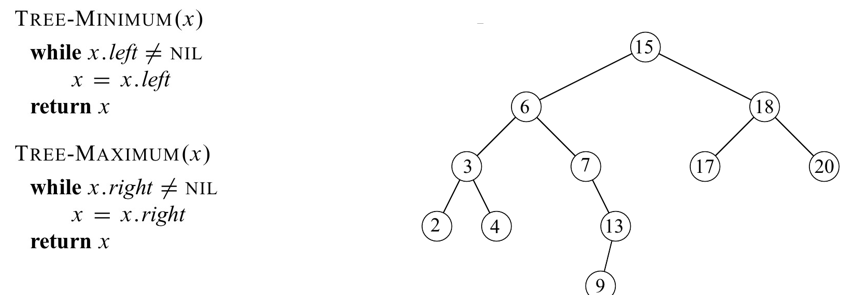
Minimum & Maximum
- 최솟값: 왼쪽 서브 트리 가장 왼쪽 노드
- 최댓값: 오른쪽 서브 트리 가장 오른쪽 노드
Successor (자식, 후임)
- 다음으로 방문할 노드
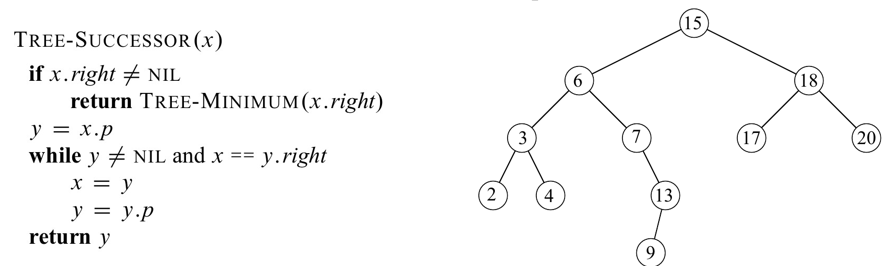
-
ex)
- 15의 후임자: 17
- 6의 후임자: 7
- 4의 흑임자: 6
- 6의 전임자: 4
Tree 전임자: Tree successor의 대칭
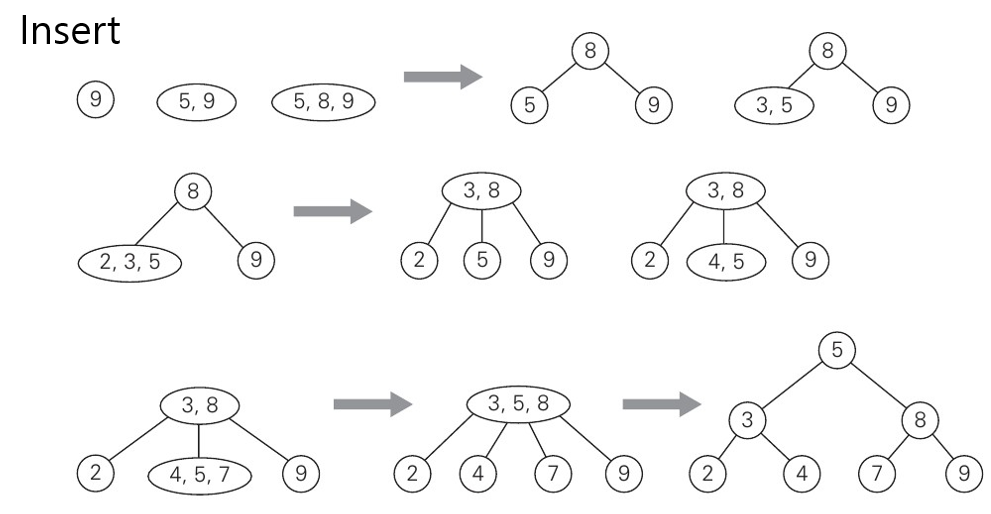
Insertion
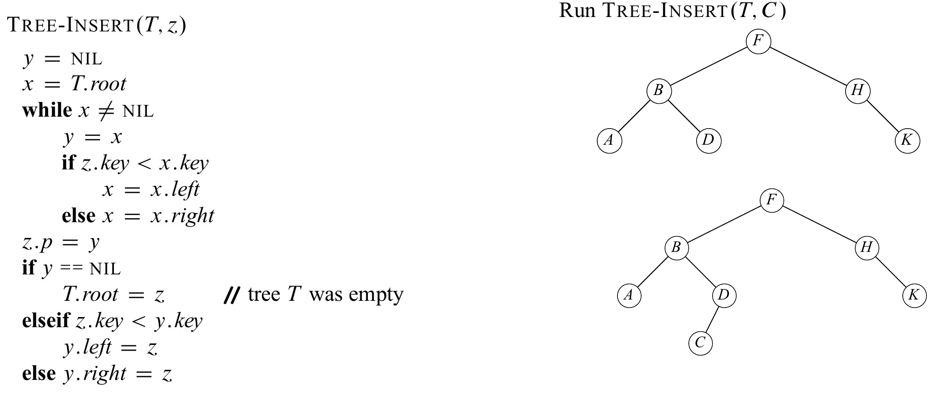
Delete
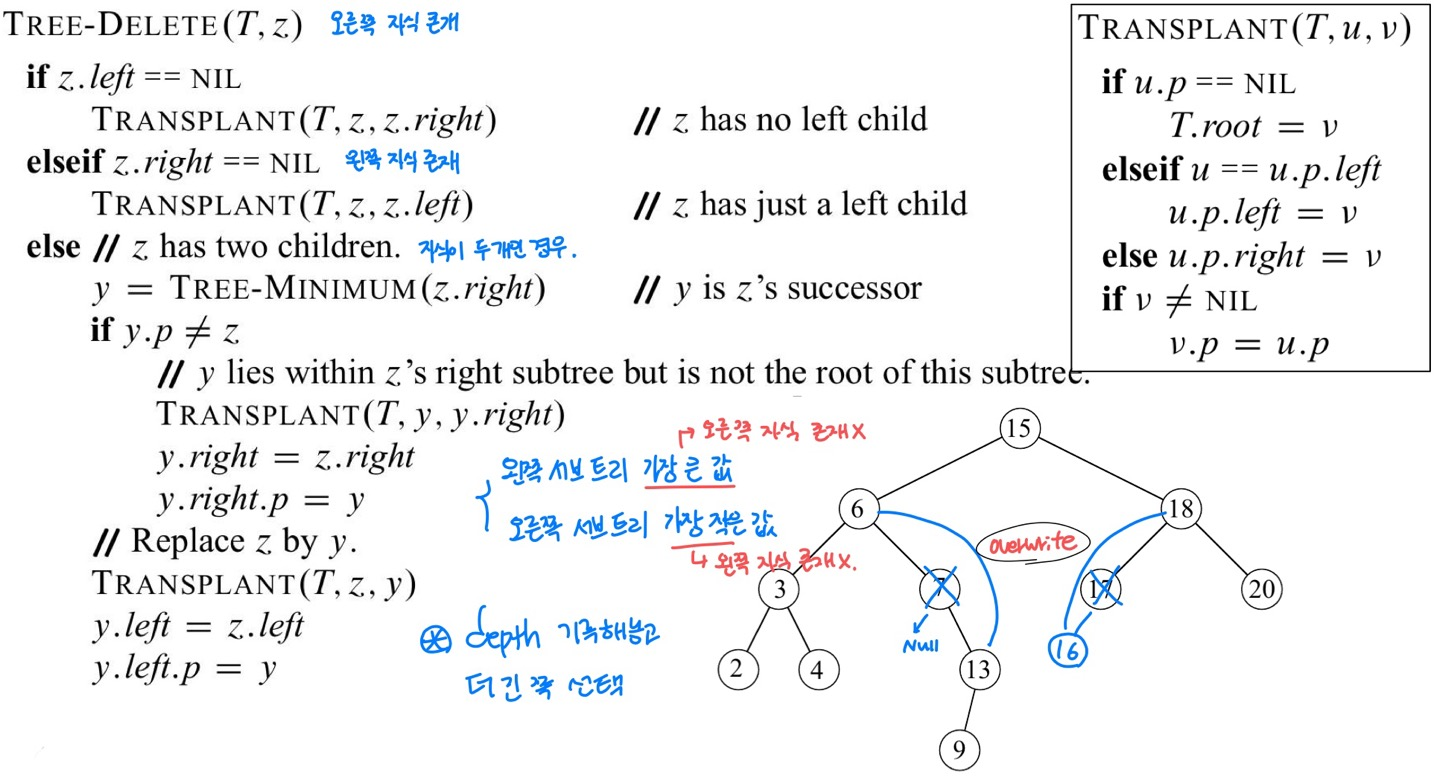
BST 효율성
- 트리 높이에 따라 달라짐
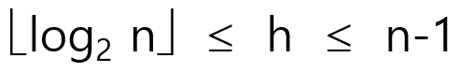
- Search, insert and delete
- worst: Θ(n)
- aberage: Θ(log n)
BST 장단점
- 장점: 순서대로 순회하면 정렬된 목록이 생성됨
- 단점: 최악의 경우 효율은 Θ(n)임
- 이를 극복하기 위해 AVL트리, 다방향 검색 트리 (2-3트리, 2-3-4트리)
- red-black tree
AVL Tree
- 이진 탐색 트리의 속성을 가진다.
- 왼쪽, 오른쪽 서브 트리의 높이 차이가 최대 1이다.
- 높이 차이가 1보다 커지면 회전(Rotation)을 통해 균형을 맞춰 높이 차이를 줄인다.
- 삽입, 검색, 삭제의 시간 복잡도가 O(log N)이다. (N : 노드의 개수)
Balance Factor(BF)
BF(K) = K의 왼쪽 서브트리의 높이 - K의 오른쪽 서브트리의 높이
- AVL트리는 모든 노드의 BF가 -1,0,1 중 하나여야 한다. 만약 이를 벗어나면 균형이 깨졌다는 것을 의미하고, 이때 회전이 필요한 것이다.
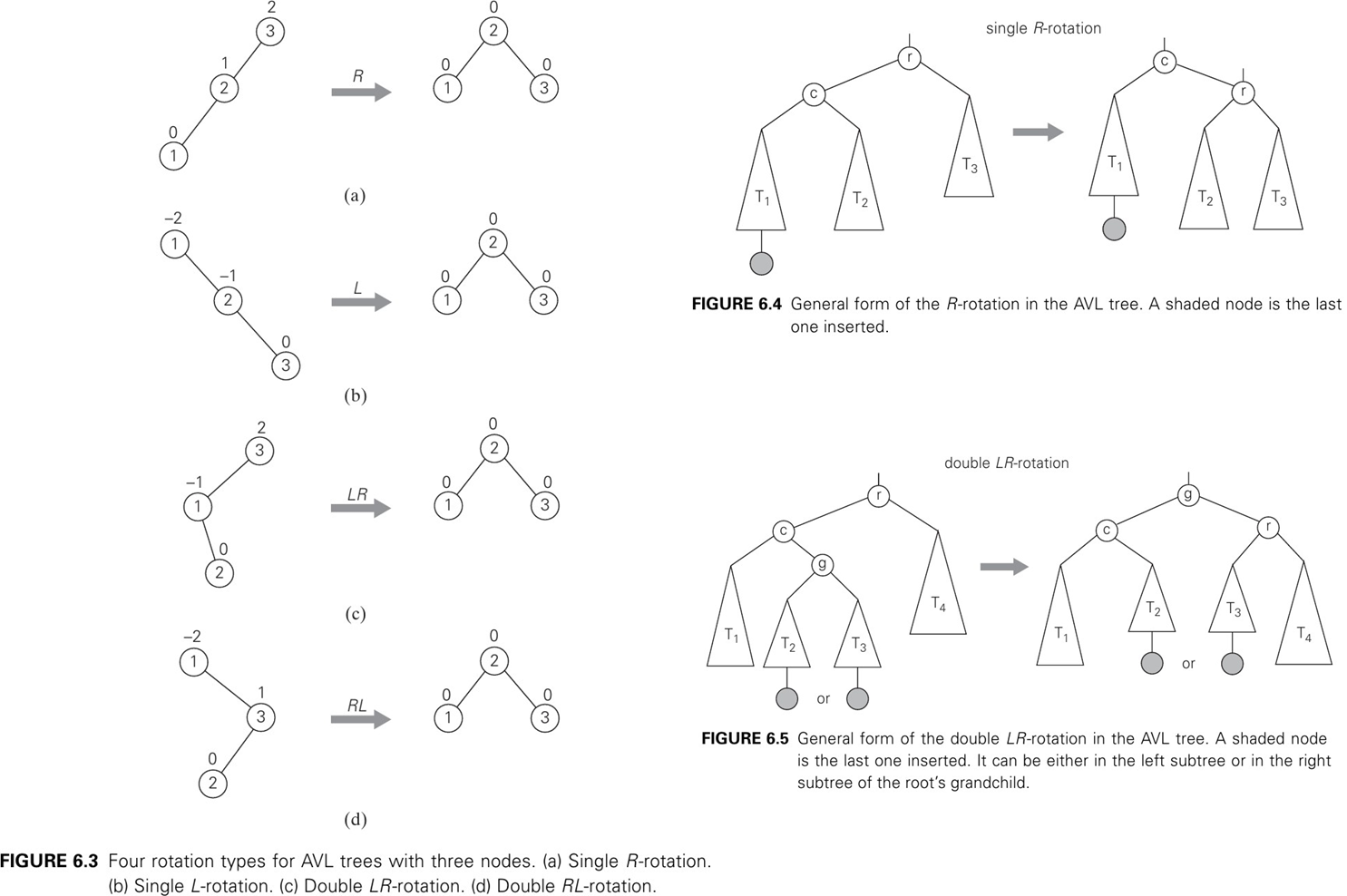
Right (a)
- 2번노드의 오른쪽 자식 노드를 3번 노드로 변경함
- 만약 2번 노드에 오른쪽 서브트리가 존재한다면 3번 노드의 왼쪽 자식 노드로 변경함
Left (b)
- 2번 노드의 왼쪽 자식 노드를 1번 노드로 변경함
- 만약 2번 노드에 왼쪽 서브트리가 존재한다면 1번 노드의 오른쪽 자식 노드로 변경함
Right Right
- BF가 -1~1을 벗어난 노드를 기준으로 오른쪽, 오른쪽 노드가 존재한다면 LL case임
- 이때 해당 노드를 기준으로 좌회전을 적용하면 불균형이 해소됨
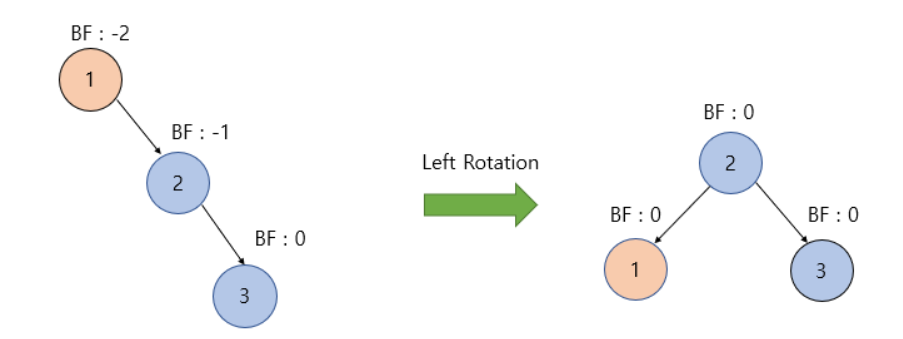
Left Left
- BF가 -1~1을 벗어난 노드를 기준으로 왼쪽, 왼쪽 노드가 존재한다면 LL case임
- 이때 해당 노드를 기준으로 우회전을 적용하면 불균형이 해소됨
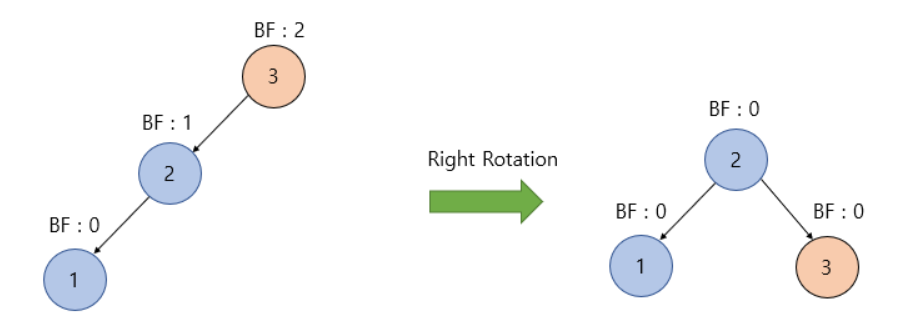
Right Left(RL) (d)
- BF가 -1~1을 벗어난 노드를 기준으로 왼쪽, 오른쪽 노드가 존재한다면 LR case임
- 이때 먼저 BF에 이상이 있는 노드의 오른쪽 자식노드를 기준으로 우회전을 진행함
- 이후 BF에 이상이 있는 노드를 기준으로 좌회전을 진행하면 불균형이 해소됨
Left Right(LR) (c)
- BF가 -1~1을 벗어난 노드를 기준으로 오른쪽, 왼쪽 노드가 존재한다면 RL case임
- 이때 먼저 BF에 이상이 있는 노드의 왼쪽 자식노드를 기준으로 좌회전을 진행함
- 이후 BF에 이상이 있는 노드를 기준으로 우회전을 진행하면 불균형이 해소됨
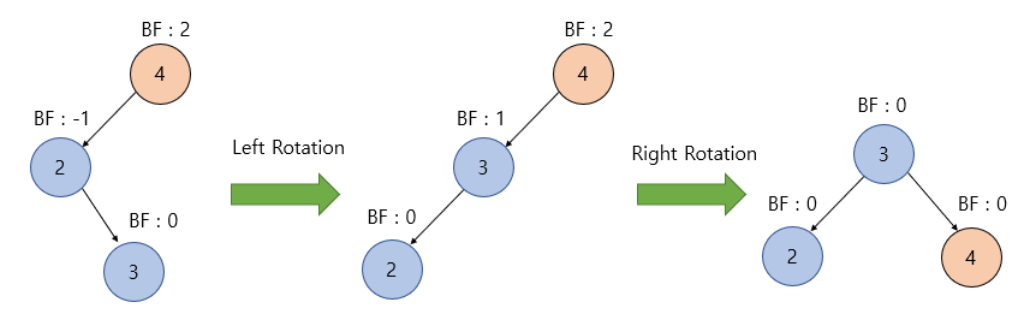
출처: https://code-lab1.tistory.com/61
2-3 Tree
2-3 Tree에는 Internal Node와 External Node의 개념이 존재합니다.
Internal Node(내부노드)는 Key가 들어있는 내부 노드이며,
External Node(외부노드)는 데이터가 들어있지 않은 노드로써 Internal Node의 Leaf Node의 자식으로 존재하는 가상의 노드입니다.
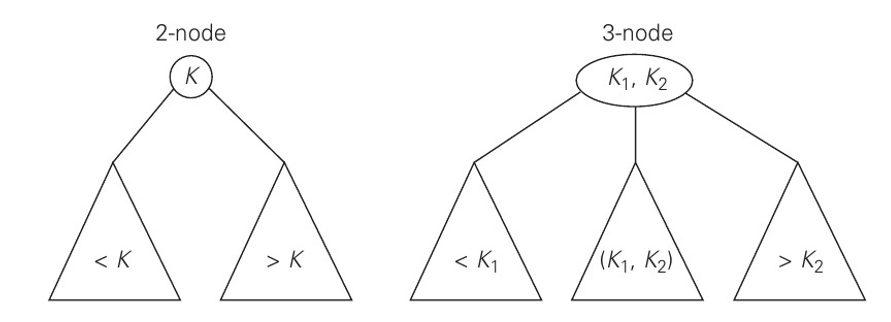
2-node: 단일 키 k를 포함해 두 개의 자식이 있음
3-node: 두 개의 키 k1 및 k2 포함
- 모든 leaf가 동일한 높이에 있어야 함
- 항상 완벽한 높이 균형이 잡혀있음
- root에서 leaf까지의 경로 길이는 모든 leaf에 대해 같음