환(Ring)
- R = <Set, Operation1, Operation2>에서 두 번째 연산은 항등원과 역원이 없을 수도 있음
- 즉 첫 번째 연산은 실제 덧셈이나 뺄셈같은 연산의 쌍이고, 두 번째 연산은 나눗셈을 사용할 수 없는 곱셈같은 단일 연산임
- 나눗셈: 역수를 곱함
환 예제) 덧셈과 곱셈의 두 연산이 정의된 집합 S는 가환 환임
-
이 집합을 S = <Z, +, x>으로 나타냄(Z는 정수 집합)
-
그렇다면, 덧셈 연산은 가환 군의 다섯가지 성질을 모두 만족함
-
또한 곱셈 연산은 덧셈 연산과 함께 사용되는 경우 분배 법칙을 만족함
-
상기 집합 S에서는 덧셈과 뺄셈, 곱셈을 모두 사용할 수 있지만 나눗셈은 사용할 수 없음
- 왜냐하면 나눗셈은 정수 집합 Z에 대해 닫힘 연산이 아니므로 두 번째 연산자의 닫힘 연산 성질을 만족하지 않음
- 집합에 있는 피연산자를 주어진 연산자로 계산한 결과도 집합 내에 있음
- 왜냐하면 나눗셈은 정수 집합 Z에 대해 닫힘 연산이 아니므로 두 번째 연산자의 닫힘 연산 성질을 만족하지 않음
-
ex) S = <N, -, x> : 닫힘 연산 성질 위배
체(Field)
- F = <Set, Operator1, Operator2>
- 특정한 성질을 만족하는 두 개의 연산이 정의된 가환 환(교환 법칙 만족)
- 첫 번째 연산은 가환 군에 대해 요구되는 다섯 가지 성질을 모두 만족함
- 두 번째 연산은 첫 번째 연산의 항등원이 역원을 갖지 않는다는 것을 제외하고 가환 군의 다섯 가지 모든 성질을 만족함
- 체는 수학에서 일반적으로 사용되는 덧셈/뺄셈, 곱셈/나눗셈 연산의 두 쌍들을 사용할 수 있는 구조임 (0으로 나누는 것 제외)
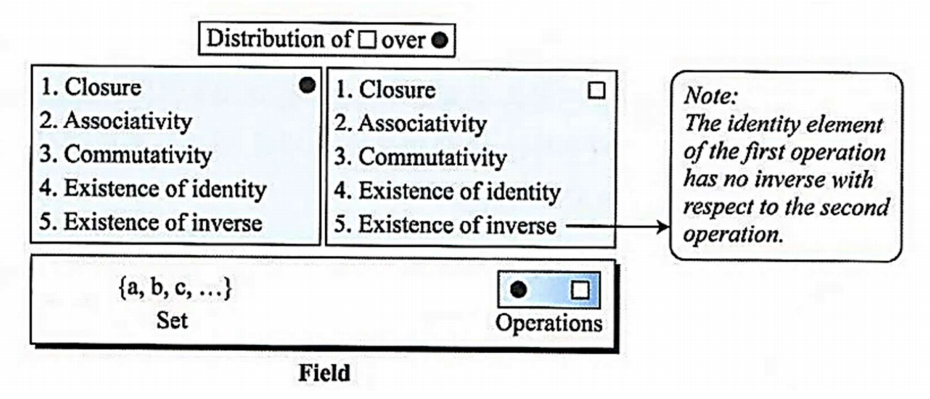
- 두 번째 연산에서의 4번, 5번
- 환에는 존재하지 않는 성질
- 항등원의 존재성
- 역원의 존재성
- 만약 곱셈이라면 나눗셈도 가능
- 항등원, 역원 (역연산 수행 가능) 존재
- 환에는 존재하지 않는 성질
cf) 곱셈 암호
- mod 곱셈 -> 역원이 없을 수도 있음
- 곱셈의 역원이 없는 원소를 키로 사용한다면?
- 복호화: 암호화의 역연산
- key값의 역원 사용
- but 역원이 존재하지 않으면 key로 사용 불가능
-> 역원이 존재하는지 (역연산이 가능한지 검사해야함)
유한 체
- 유한 개의 원소를 갖는 체로, 암호학에서 주로 사용되는 대수 구조
갈로아 체
- 표기: GF(p^n)
- p^n개의 원소를 갖는 유한 체
- p는 소수
- n은 양의 정수
GF(p) 체
- 갈로아 체에서 n = 1인 경우
- 두 개의 산술 연산(덧셈과 곱셈)을 가지는 Z = { 0, 1, 2, ..., p-1}가 될 수 있음
- 이 집합에서 각각의 원소들은 덧셈 역원과 0이 아닌 원소에 대해 곱셈 역원을 가짐 (0에 대한 곱셈의 역원은 없음)
- 갈로아 체와 GF(p)체는 암호학에서 널리 활용되는 대표적인 체임
예제1) 암호 분야에서 가장 널리 쓰이는 체는 집합 {0, 1}과 두 개의 산술 연산 (덧셈과 곱셈)을 갖는 GF(2)체임
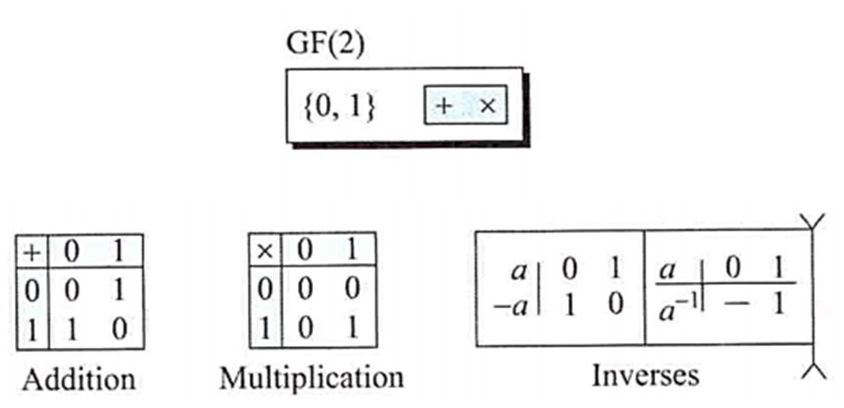
- 집합은 2진수 혹은 비트 (0과 1)로 표현되는 두 개의 원소만 가짐
- 덧셈 연산은 실제로 두 2진수들에 사용하는 XOR연산임
- 곱셈 연산은 두 2진수들에 사용하는 AND연산임
- 덧셈과 뺄셈 연산은 XOR연산으로 같음
- 곱셈과 나눗셈 연산은 AND연산으로 같음
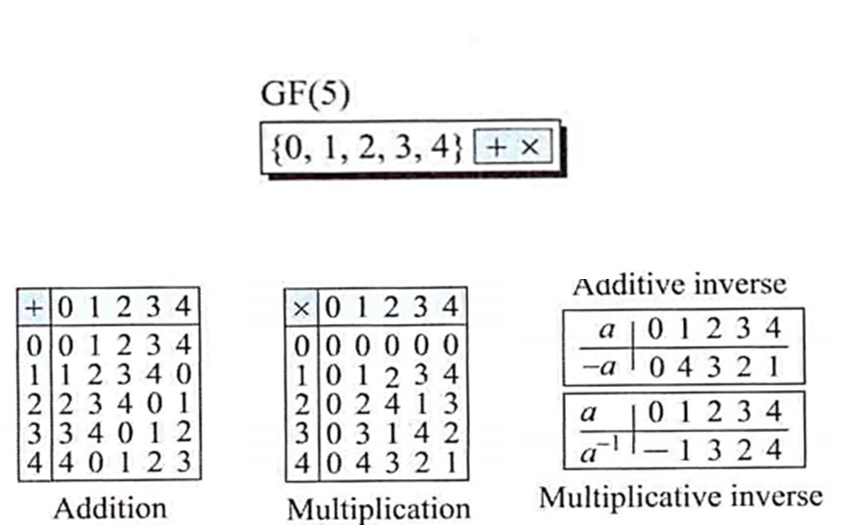
예제2) 덧셈과 곱셈 연산을 같는 Z 위에 GF(5)체를 정의해라
- GF(5)의 집합과 연산을 정의
- 덧셈 연산에 대한 Z에서의 덧셈표 정의
- 곱셈 연산에 대하 Z에서의 곱셈표 정의
- 덧셈 연산에 대한 역원(inverse) 정의
- 곱셈 연산에 대한 역원 정의
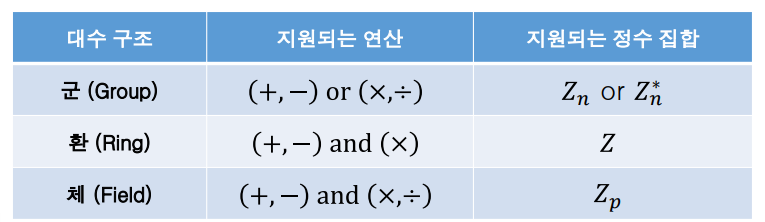
대수 구조 요약
- 세 가지 대수 구조 (군/환/체) 연구는 덧셈/뺄셈/곱셈/나눗셈과 같은 비슷한 연산이 정의된 집합을 사용할 수 있도록 해줌
- 군은 하나의 연관된 연산의 쌍을 지원함
- 환은 하나의 연관된 연산의 쌍과 또 다른 단일 연산을 지원함
- 체는 연산의 두 쌍을 지원함