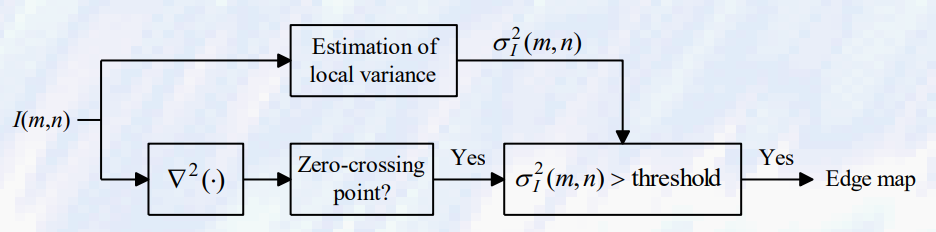
- 에지들은 I^2(m, n)의 zero-crossing point(제로 교차점)에서 찾을 수 있음
- Laplacian 연산자는 일반적으로 영상의 로컬 분산이 작은 영역에 나타나는 많은 거짓 에지 등고선(false edge ㅇ)을 생성함
- 이런 많은 거짓 등고선을 제거하는 방법은 로컬 분산 σ^2이 충분히 커야한다는 것임
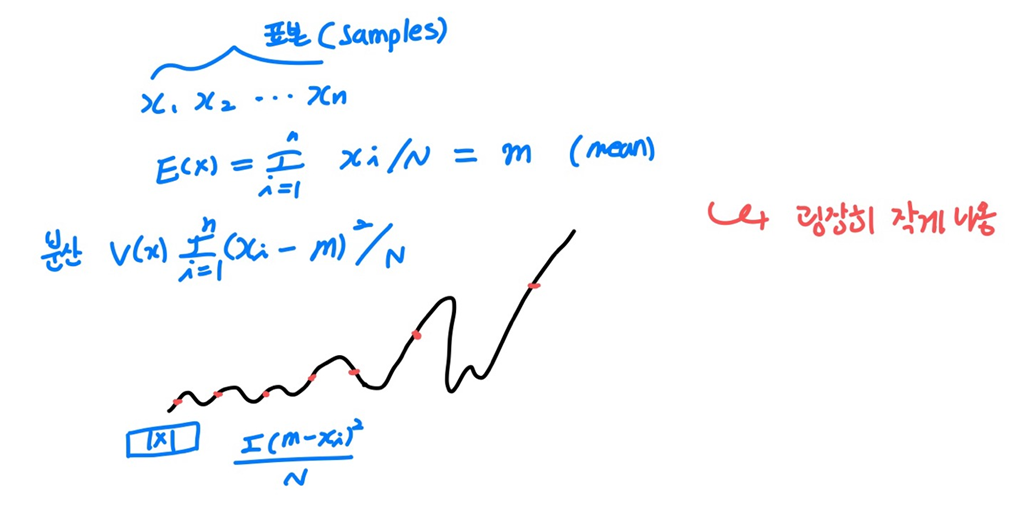
중요한 정보는 가운데에 주로 있음
thersholding 국부 지역의 가운데 값을 사용함
1차원: sobel
2차원: Laplacian
zero-crossing은 굉장히 조밀하게 나옴
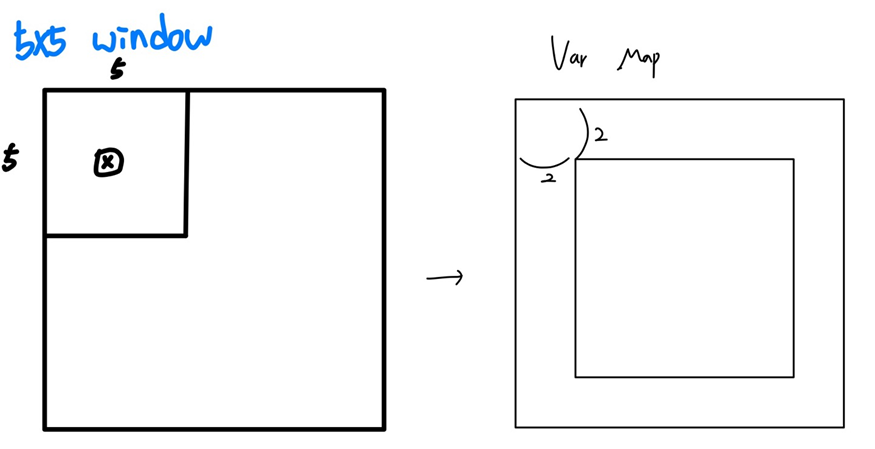
for (int i = w/2; w < H - w/2; i++) {
for (int j = w/2; j < W - w/2; j++) {
float tmp_s = 0;
for (int k = -w/2; k <= w/2; k++)
for (int l = -w/2; l <= w/2; l++)
tmp_s += inImg[i+k][j+l];
tmp_s = tmp_s / (w * w);
float tmp_v = 0;
for (int k = -w/2; k <= w/2; k++)
for (int l = -w/2; l <= w/2; l++)
tmp_v += (inImg[i+k][j+l] - tmp_s) * (inImg[i+k][j+l] - tmp_s);
tmp_v /= (w * w);
var[i][j] = tmp_v;
}
}- Local Variance : thresholing으로 국부 분산 값들의 평균을 사용함
- Global Variance
-> Variance: 큰 변화가 있는지 알려줌
- Gradient -> sobel
- 2nd-order(Laplacian) => Canny operator
- 1px 두께 edge, 연결도 시켜줌, 영점에 가장 가까운 위치도 찾아줌
2차 미분: 크기 상관 없음 변곡점이 중요함!
부드럽게 처리해서 다시 미분해보자
미세한 edge 줄이기
1. 분산
2. LPF
Smoothing(Average) -> 미세한 경계(edge)가 zero가 됨!
평균처리: 표준 정규 분포 곡선 사용 -> Gaussian Fuction
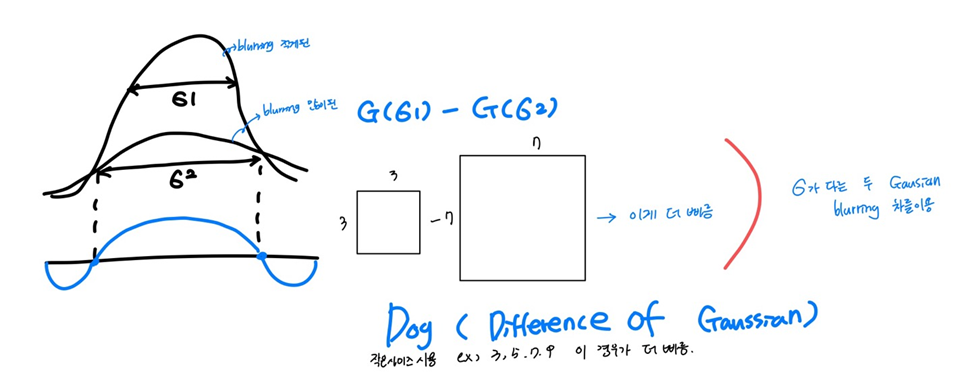
블러링이 많이 된 가우시안, 블러링이 적게 된 가우시안을 비교함
G(σ1) - G(σ2)를 한 값이나 위의 사진에 있는 예시처럼 박스 필터를 사용해서 구한 차이 값이나 동일함 그러나 박스 필터 값을 사용하는 게 훨씬 빠름
정리:
특징 추출: 경계 -> 기울기, 미분
1. Gradient operator
2. Laplacian operator -> too 민감 -> local variance로 thresholding -> edge를 연결하고 자잘한 경계를 없애기 위해 -> LOF or DOG (box filter를 사용해 blurring차이를 구하는 방법이 훨씬 빠름)
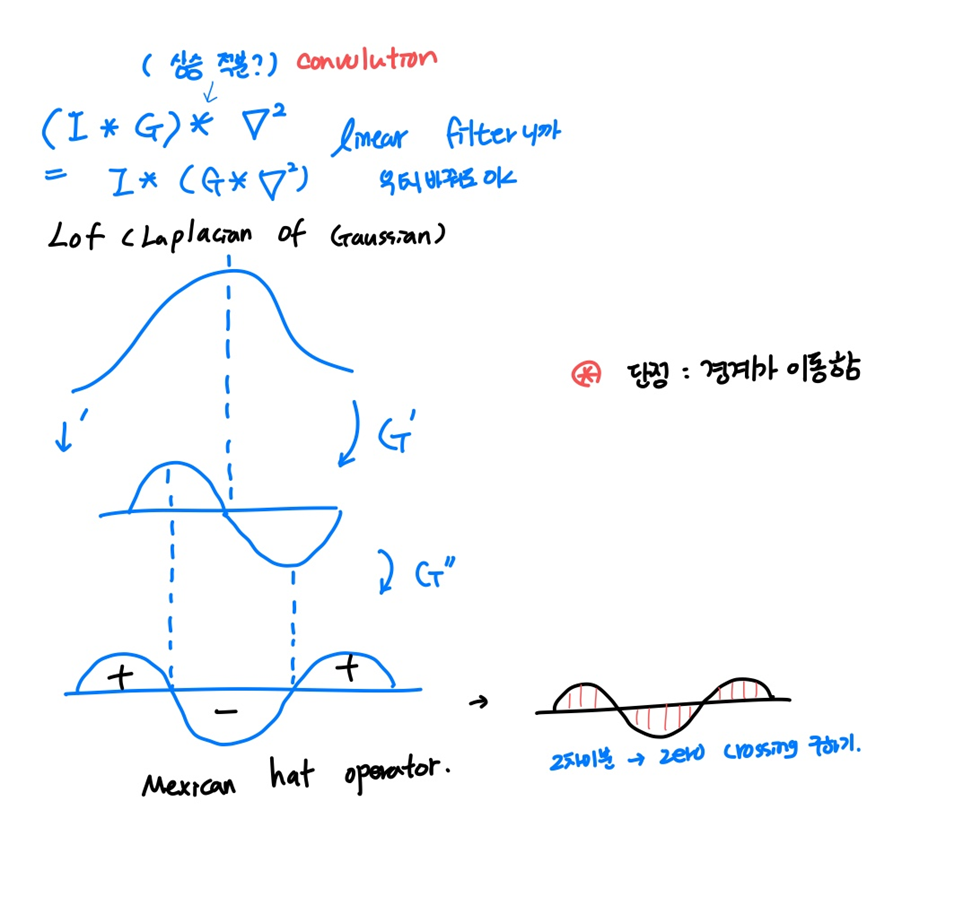
Laplacian of Gaussian(LOG)
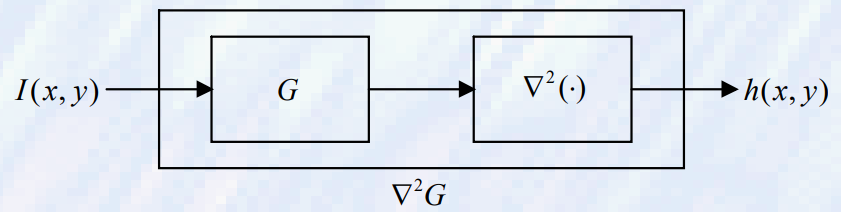
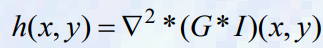
-
가우스와 라플라시안의 합성곱 (상승 적분)
-
G: Gaussian smoothing operator
-
모양 때문에 Mexican hat operator라고도 불림
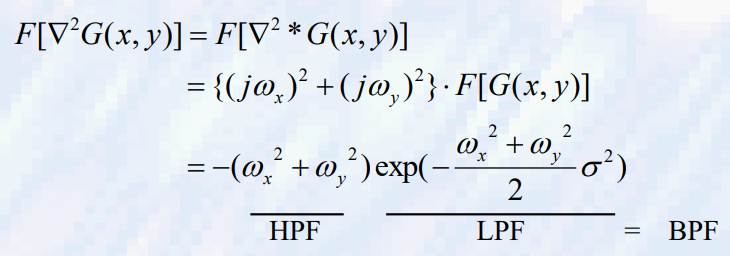
- LOG는 가우스 함수의 σ에 해당하는 대역 통과 필터(BPF)
- θ가 큰 값을 가질 경우 더 많은 흐림과 강한 에지를 얻을 수 있음
- 그렇지 않으면 픽셀 이동이 적은 미세한 가장자리와 작은 디테일이 생성됨
Separable Decomposition of LOG
updating...
Nonlinear Gradient and Laplacian Operators
Nonlinear Gradient

- W = MxM window
- noise와 granularity(미세함)에 민감하지 않음 -> 좋은 거!
- valley 뿐만 아니라 peak도 감지함

- 곱셈이 없기 때문에 구현이 매우 쉬움
- 또한 형태학적 경사 연산자와 밀접한 관계가 있으며 unbias 특성(?)을 가지고 있음
Valley Detectors and HVS-based Sketch Operators
Valley detectors
-
국소 휘도 최소인 계곡의 전형적인 프로파일
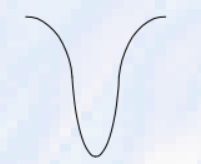
-
실질적으로 valley detector은 valley 뿐만 아니라 edge도 감지하는 것이 바람직함
- 한 가지 해결책은 이미지와 선형적으로 결합될 때 valley에 대한 최적의 반응을 가지지만 스텝 에지에 대한 잔류 반응을 갖는 단일 연산자를 사용하는 것임
HVS-based sketch operators
- 인간의 관찰자는 밝은 지역의 관찰자보다 어두운 지역의 가장자리(edge)와 계곡(valley)에 더 민감함
따라서 인간의 시각 시스템과 유사한 방식으로 물체를 인식하고 분석하려면 국소 강도에 따라 스케치 특징(valley와 edge)을 추출해야 함 - Entropy Operator
- 엔트로피 연산자는 각 픽셀에 대한 MxM window의 강도 엔트로피를 계산함
- 픽셀의 국소 확률은 다음과 같이 정의됨
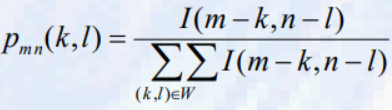
- entropy at (m,n)
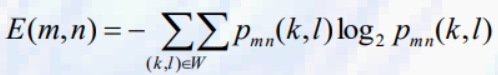


- E(에지 또는 계곡 픽셀) < E(평평한 영역의 픽셀)의 특성을 가지고 있음
- 또한 국소 강도에 의존하기 때문에 어두운 영역의 가장자리를 매우 잘 추출함
- 즉, 대비가 동일한 두 단계 에지의 경우
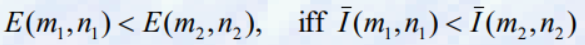
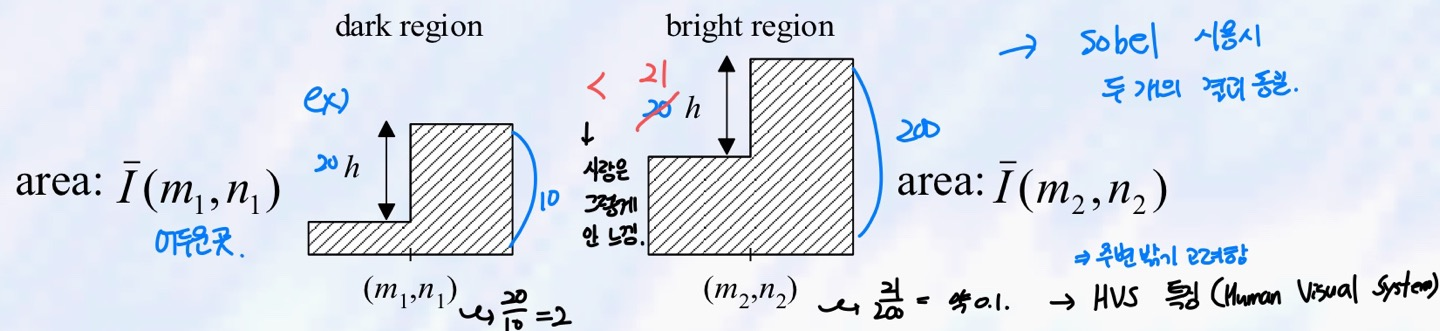
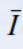
: 국소 강도의 합
- 에지 굵은 선을 추출하고 로그 연산에는 많은 양의 연산이 필요함
DP and DIP Operator
DP(Difference of probability)
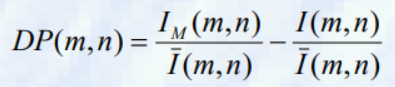
- non-linear gradient
- 여기서 Im(m,n)은 MxM 창의 최대 강도임
- 그것의 형태는 강도의 합을 나누는 것을 제외하면 비선형 기울기와 매우 유사함
- DP는 취한 차이로 인해 계곡과 가장자리에서 잘 반응할 뿐만 아니라, 지역 강도에 의존함
- 강도 합계의 사용. 그러나 valley 자체뿐만 아니라 valley의 이웃을 추출하는 단점이 있음(선이 생성됨)
이 문제를 제거하기 위해 DP를 개혁하면, DIP(역확률의 차이)는 다음과 같이 정의된다
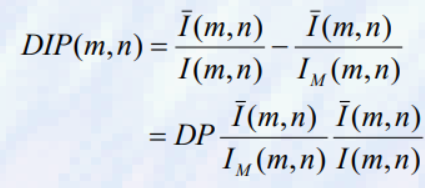
- I(m,n)는 이웃보다 valley에서 작기 때문에 valley 자체에서 DIP의 값이 훨씬 커서 valley을 얇게 추출함
