[TIL]230602 - 알고리즘 13주차: Greedy Algorithm
Greedy vs. Dynamic Programming
- 0-1 배낭 문제: Greedy로 해결할 수 없음
- 예) 가게를 털던 도둑이 n개의 물건을 찾았습니다. i번째 아이템은 $vi의 가치가 있고 무게는 파운드입니다. 그는 배낭에 최대 W파운드까지 실을 수 있습니다. 그러면, vi, wi, W는 정수입니다. 그는 어떤 물건을 가져가야 합니까?
- 총 중량이 ≤ W인 항목의 가장 귀중한 부분 집합을 찾음
- 물건을 가져가야 할지 안 가져가야 할지도 모름. 그것을 가져갈 수가 없음
- 부분 배낭 문제: Greedy로 해결 가능
- 0-1 배낭 문제처럼, 하지만 항목의 일부를 차지할 수 있음
공통점과 차이점
- 둘 다 최적의 하부 구조를 가지고 있습니다.
- 그러나 부분 배낭 문제는 탐욕스러운 선택의 속성을 가지고 있고 0-1 배낭 문제는 그렇지 않습니다.
- 분수 문제를 해결하려면 값/무게: vi/wi를 기준으로 항목의 순위를 지정합니다.
- 모든 i에 대해 vi / wi ≥ v(i+1) /w(i+1)
부분 배낭 문제 예시

- 실행 시간: 정렬 - O(nlgn), 이후 O(n).
허프만 코드 (Application of Greedy Algorithm)
- 데이터 압축 기술 - 널리 사용되고 효과적
- 문제: 정보 손실 없이 파일을 압축하는 방법은 무엇입니까?
- 압축은 공간뿐만 아니라 시간도 절약함
- 이진 문자 코드 사용
- 탐욕 알고리즘을 적용하여 허프먼이 발명한 최적의 접두사 코드
- 이 알고리즘은 최적의 코드에 해당하는 트리 T를 상향식으로 구축함
- 그것은 일련의 |C| 잎으로 시작하고 최종 트리를 만들기 위해 |C| -1 병합 작업의 시퀀스를 수행함
- 키를 누른 최소 우선순위 큐 Q는 함께 병합할 가장 빈도가 낮은 두 개체를 식별하는 데 사용됨
- 두 개체의 병합 결과는 병합된 두 개체의 주파수 합계인 주파수를 가진 새 개체임
허프만 코드 예제

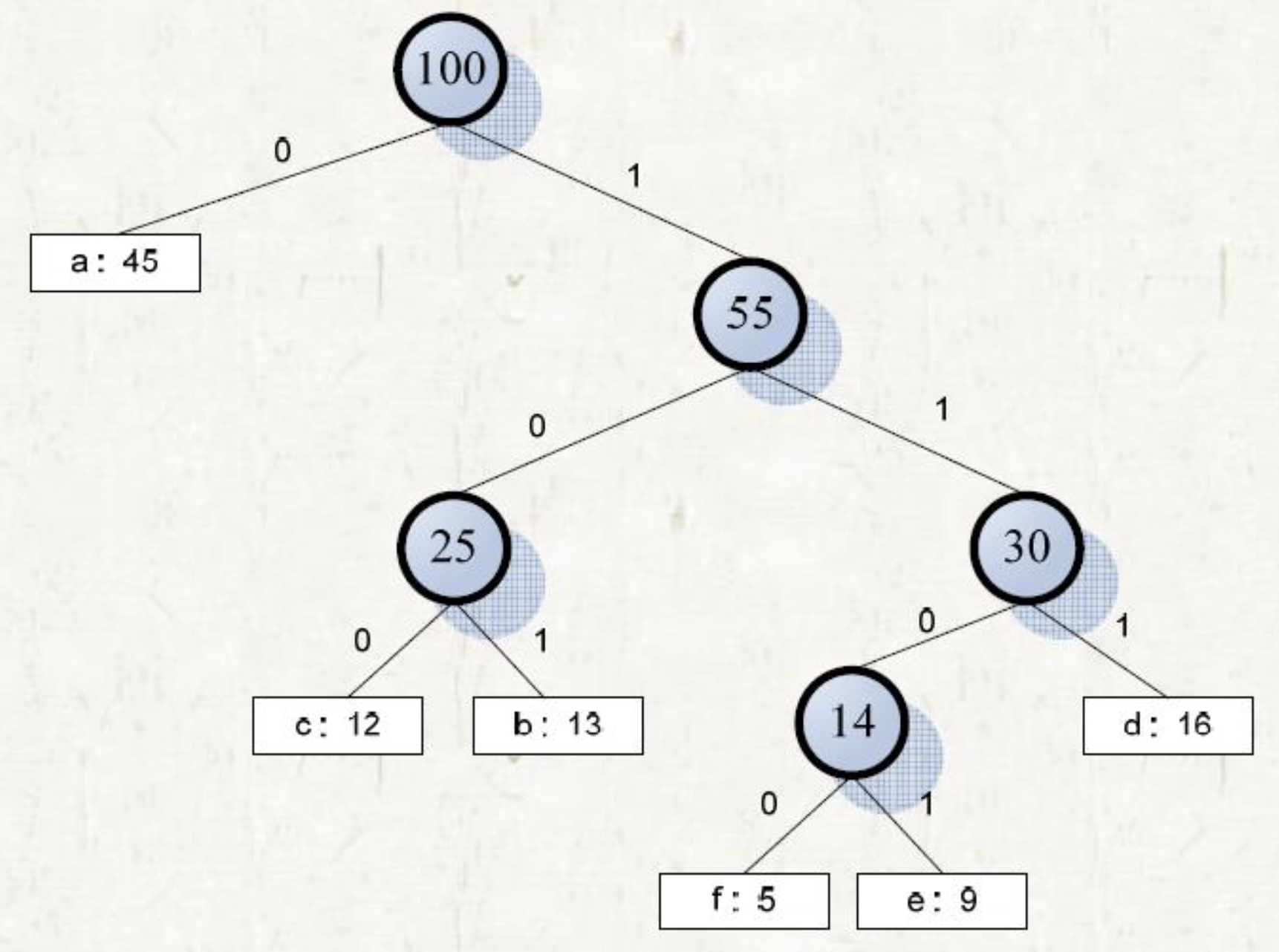
허프만 코드 분석
- Q가 이진 최소 힙으로 구현된다고 가정
- n개 문자 집합 C의 경우,
- BUILD-MIN-HEAP 절차를 사용한 Q(라인 2) – O(n)의 초기화
- 루프(3~8행)의 경우 => O(nlgn)
- 정확한 n-1회 실행
- 각 힙 작업 – O(lgn)
- n자 집합의 총 실행 시간 -> O(nlgn)





