[백준]10830번 행렬 제곱

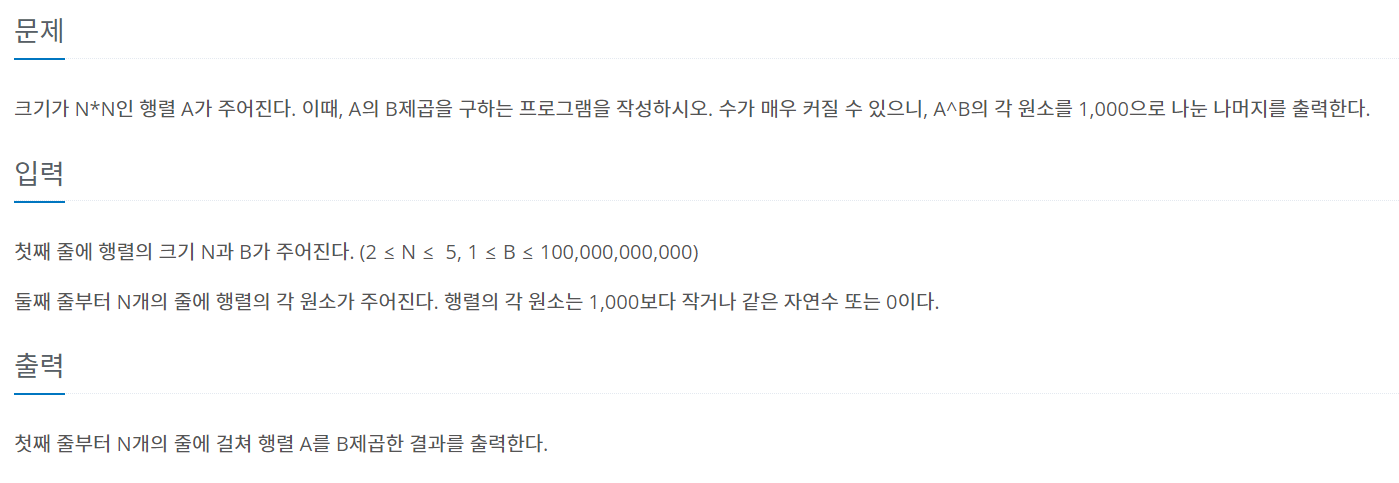
행렬의 곱을 구해서 분할 정복 (지수 법칙, 모듈러 정리)를 통해 해결할 수 있음. 그러나 행렬의 곱을 구하는 방법에서 문제가 발생했음.

행렬의 곱을 구하는 것까지는 성공했으나 오류가 발생함.
원인은 모듈러 정리를 적용해주지 않았기 때문임.
long 타입의 숫자가 아닌 행렬을 통한 분할 정복이었기 때문에 어디서 모듈러 정의가 적용되는지 애매했음.

각 행렬의 원소에 모듈러 정의를 적용함.
행렬의 곱을 통해 원소 값을 구한 다음 임의의 나머지 (해당 문제에서는 행렬의 각 원소가 1000보다 작거나 같은 자연수 또는 0이므로 mod를 1000으로 정의함.)

또한 지수(B) 타입을 long으로 해줘야한다는 것 유의해야함!!(범위에 따라 타입을 잘 정해줘야 함)

static int[][] squared(int[][] A, int[][] B) {
        int[][] result = new int[n][n];
        for (int i = 0; i < n; i++) {
            for (int j = 0; j < n; j++) {
                for (int k = 0; k < n; k++) {
                    result[i][j] += A[i][k] * B[k][j];
                    /*
                    모듈러 정리
                     */
                    result[i][j] %= mod;
                }
            }
        }
        return result;
    }

---

제출 코드

public class G10830 {
    final static int mod = 1000;
    public static int n;
    public static int[][] procession;

    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        StringTokenizer st = new StringTokenizer(br.readLine());
        n = Integer.parseInt(st.nextToken());
        long expo = Long.parseLong(st.nextToken()); //타입 주의!!

        int[][] procession = new int[n][n];

        for (int i = 0; i < n; i++) {
            st = new StringTokenizer(br.readLine());
            for (int j = 0; j < n; j++) {
                procession[i][j] = Integer.parseInt(st.nextToken()) % mod;
            }
        }

        int[][] ans = pow(procession, expo);

        StringBuilder sb = new StringBuilder();
        for (int i = 0; i < n; i++) {
            for (int j = 0; j < n; j++) {
                sb.append(ans[i][j]).append(" ");
            }
            sb.append("\n");
        }
        System.out.println(sb);


    }

    static int[][] squared(int[][] A, int[][] B) {
        int[][] result = new int[n][n];
        for (int i = 0; i < n; i++) {
            for (int j = 0; j < n; j++) {
                for (int k = 0; k < n; k++) {
                    result[i][j] += A[i][k] * B[k][j];
                    /*
                    모듈러 정리
                     */
                    result[i][j] %= mod;
                }
            }
        }
        return result;
    }

    static int[][] pow(int[][] A, long expo) {
        if (expo == 1L) {
            return A;
        }

        int[][] temp = pow(A, expo/2);
        temp = squared(temp, temp);

        if (expo % 2 == 1L) {
            temp = squared(temp, A);
        }

        return temp;
    }
}

[출처] https://st-lab.tistory.com/251