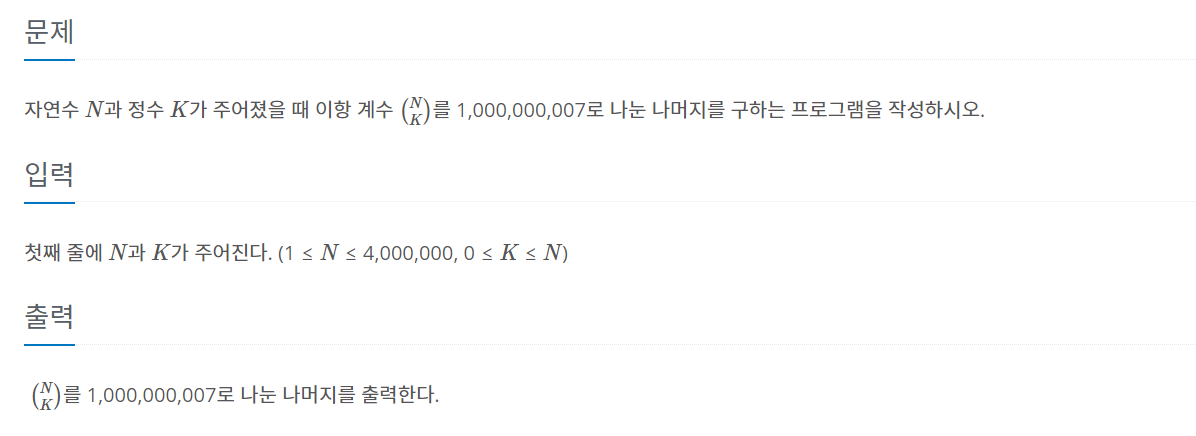
이 문제를 해결하기 위해서는 모듈러 연산과 페르마의 소정리 개념이 필요함
먼저 이항 계수를 구하는 방법은 이와 같다.
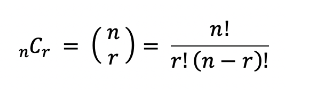
문제에서 주어지는 입력은 너무 크기 때문에 결국 모듈러의 연산 공식을 활용해야한다.
여기서 중요한 점은 모듈러 연산에서 나눗셈 연산이 없다는 것이다!
즉, 나눗셈(분수 꼴)의 수에 대한 모듈러 연산은 분배법칙을 적용할 수 없다.
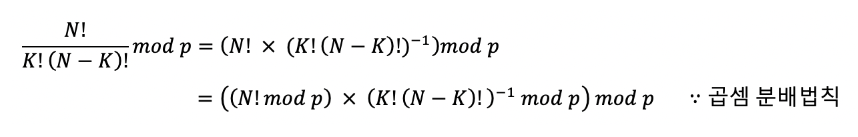
여기서 (K!(N-K)!)의 역수를 구하는 것이 관건이다. 이를 해결하기 위해서 페르마의 소정리를 적용하는 것이다.
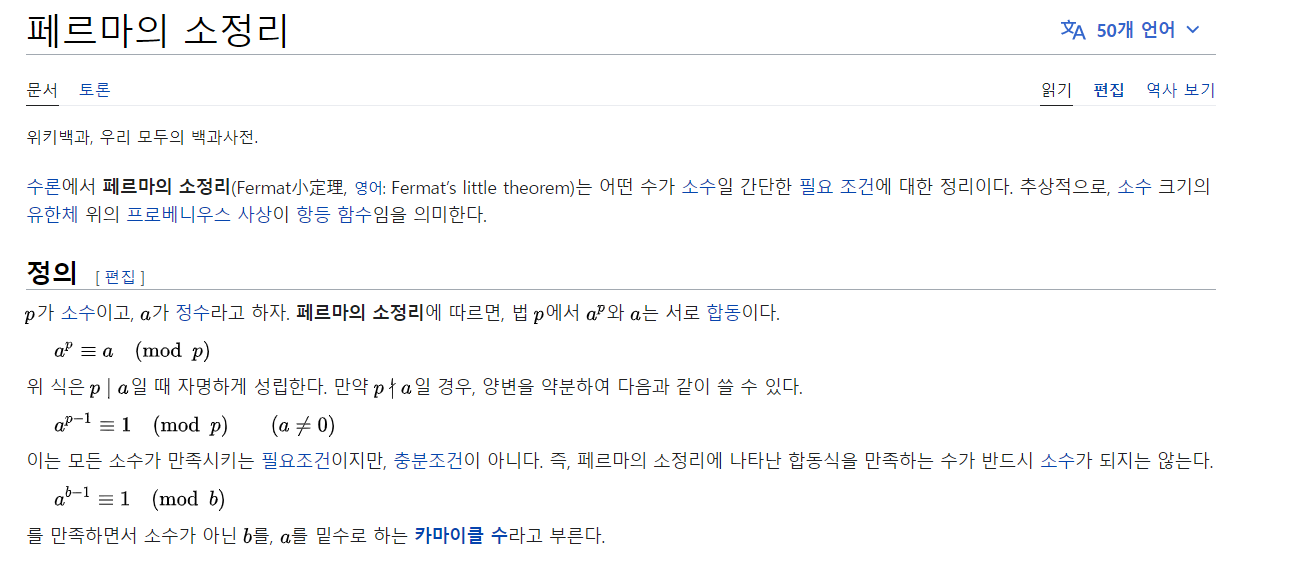

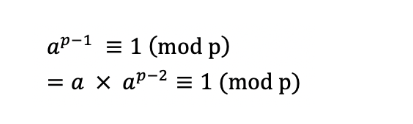
위의 정리를 통해 아래와 같이 나타낼 수 있다.
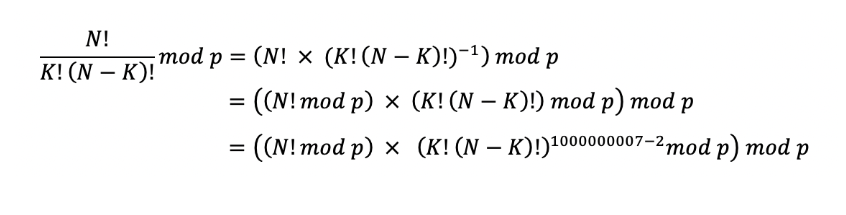
그렇다면 분할 정복은 어디서 쓰이는 것일까?
역수를 구하는, (N-K)를 p-2 제곱하는 알고리즘에서 사용된다.
제출 코드
1. 런타임에러
public class Main {
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
int n = 0, k = 0;
while (st.hasMoreTokens()) {
n = Integer.parseInt(st.nextToken());
k = Integer.parseInt(st.nextToken());
}
int res = 0;
res = 이항계수(n, k);
System.out.println(res % 1000000007);
}
static int factorial (int n) {
int ans = 1;
for (int i = 2; i <= n; i++) {
ans *= i;
}
return ans;
}
static int 이항계수(int n, int k) {
return factorial(n) / factorial(k) / factorial(n-k);
}
}
이 풀이는 long 범위를 넘어서 잘못된 값이 입력될 수도 있기 때문에 런타임 에러가 난 것으로 예상됨.
2. 실패
원인
static long factorial (long n) {
long ans = 1L;
for (long i = 2; i <= n; i++) {
ans *= i;
}
return ans;
}여기서 반환값에도 모듈러 정리를 적용시켜줘야하는데 그러지 않았기 때문에 틀린 것으로 예상함.
3. 제출 코드
public class Main {
public static long C = 1000000007;
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
long n = Long.parseLong(st.nextToken());
long k = Long.parseLong(st.nextToken());
long numerator = factorial(n);
long denominator = factorial(k) * factorial( n-k) % C;
System.out.println(numerator * pow(denominator, C-2) % C);
}
static long factorial (long n) {
long ans = 1L;
while (n > 1) {
ans = (ans * n) % C;
n--;
}
return ans;
}
static long pow(long A, long exponent) {
if (exponent == 1) {
return A % C;
}
long temp = pow(A, exponent / 2);
if (exponent % 2 == 1) {
return (temp * temp % C) * A % C;
}
return temp * temp % C;
}
}

