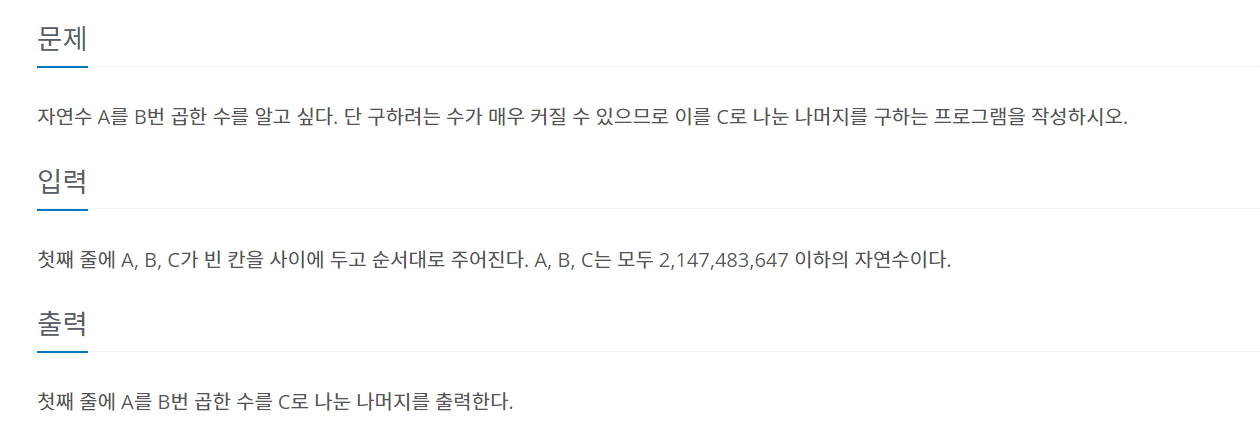
11401번 이항 계수3 문제를 해결하기 위해 이 문제를 먼저 풀어보았다.
이 문제를 해결하기 위해서는 지수 법칙과 모듈러 성질이 필요하다.
-
지수 법칙
a^(m+n) = a^m * a^n -
모듈러 성질
(a b) mod C = (a mod C * b mod c) mod C
-> (a % C x b % C) % C
지수 법칙은 지수를 반으로 나눌 때 이용함
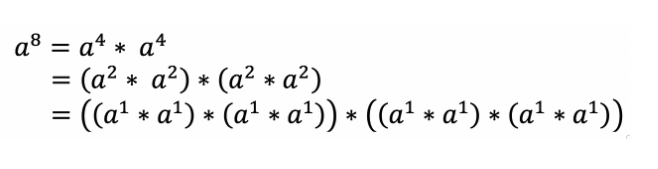
만약 지수가 홀수라면 a를 한 번 더 곱해주면 됨
아래와 같은 형태가 됨
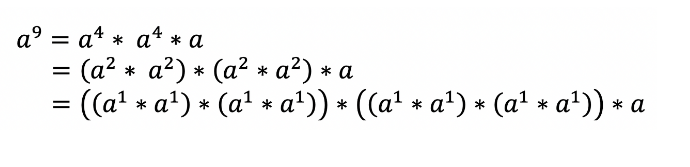
다음으로 모듈러 성질을 이용해야하는데 여기서 그냥 "%C"만 붙여주면 해결할 수 없다.
long pow(long A, long exponent) {
if(exponent == 1) {
return A % C;
}
/*
* 중략
*/
if(exponent % 2 == 1) {
return temp * temp * A % C;
}
return temp * temp % C;
}밑이 2,147,483,647(2^31 - 1)이라면 ??
(2^31) (2^31) (2^31) = 2^94 이렇게 되면 long형 범위를 넘어간다.
즉 잘못된 값으로 계산이 되어버려 틀리게 된다.
그래서 모듈러 합동 공식을 알고 있어야 한다!!!
이를 고려해서 리턴값에 모듈러 연산을 해주면 된다.
long pow(long A, long exponent) {
if(exponent == 1) {
return A % C;
}
/*
* 중략
*/
if(exponent % 2 == 1) {
return (temp * temp % C) * A % C;
}
return temp * temp % C;
}제출 코드
public class Main{
public static long C = 0;
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine(), " ");
long 밑 = 0, 지수 = 0;
while (st.hasMoreTokens()) {
밑 = Long.parseLong(st.nextToken());
지수 = Long.parseLong(st.nextToken());
C = Long.parseLong(st.nextToken());
}
System.out.println(pow(밑, 지수));
}
public static long pow(long A, long exponent) {
if (exponent == 1) {
return A % C;
}
long temp = pow(A, exponent / 2);
if (exponent % 2 == 1) {
return (temp * temp % C) * A % C;
}
return temp * temp % C;
}
}

