[백준]9251번 LCS

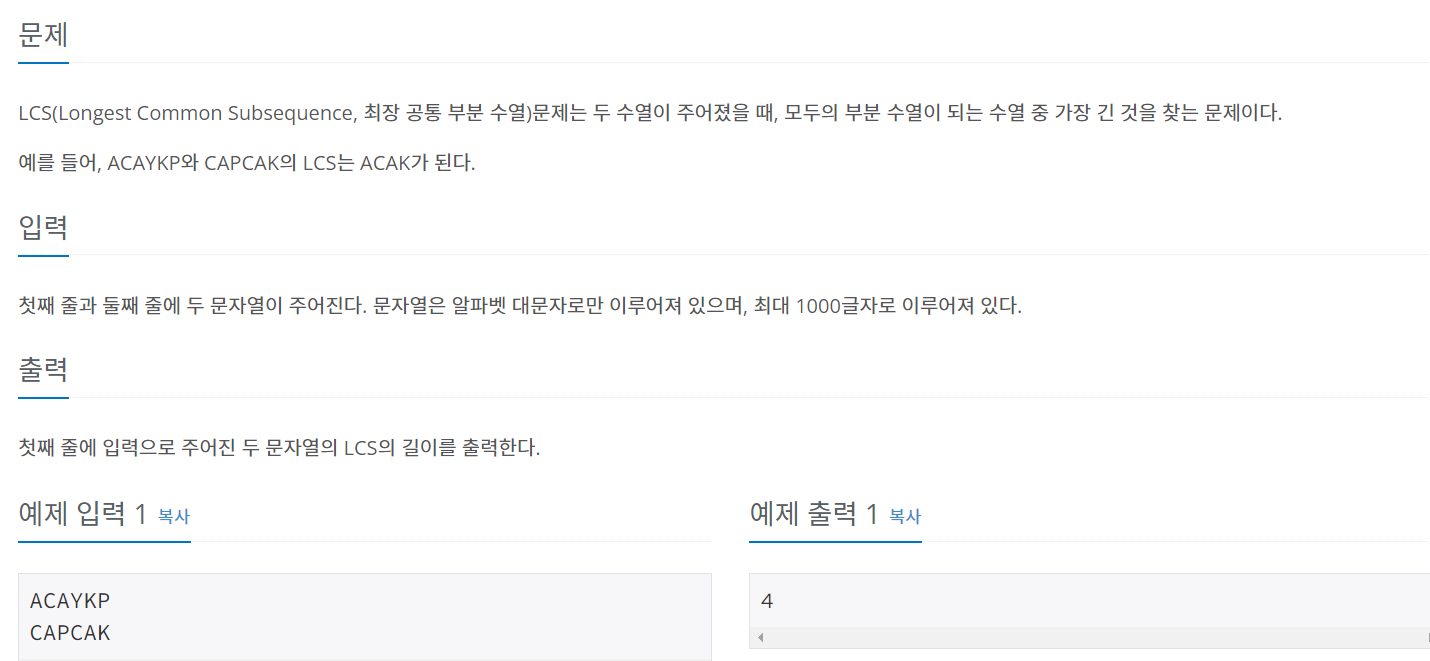
LCS 최장 공통 부분 수열 문제

점화식

if i == 0 or j == 0:  # 마진 설정
	LCS[i][j] = 0
elif string_A[i] == string_B[j]:
	LCS[i][j] = LCS[i - 1][j - 1] + 1
else:
	LCS[i][j] = max(LCS[i - 1][j], LCS[i][j - 1])

1. 문자열 a, b의 한 글자씩 비교한다.
2. 두 문자가 다르다면 lcs[i-1][j]와 lcs[i][j-1]중 큰 값을 저장한다.
3. 두 문자가 같다면 lcs[i-1][j-1] +1을 저장한다.
4. 위 과정을 반복한다.

<2>
현재 문자를 비교하는 과정 이전의 최대 공통 부분수열은 계속 유지됨.
현재 문자를 비교하는 과정 == lcs[i-1][j]와 lcs[i][j-1]

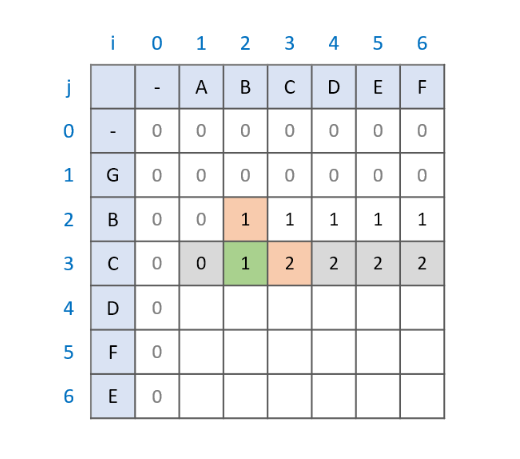
AB와 GBC를 비교하는 예시
최대 공통 부분 수열이 B라는 것을 알기 위해서는
문자열 A와 GBC를 비교하는 과정에서 문자열 AB와 GB를 비교하는 과정이 필요함. AB와 GB는 최대 공통 부분 수열이 B임을 확인했기 때문에 문자열 AB와 GBC의 최대 공통 부분 수열 역시 B가 된다.

<3>
ABC와 GBC의 최장 공통 부분 수열을 구하기 위해서 AB와 GB의 최장 공통 부분 수열에 +1을 해주면 되기 때문에 이를 점화식으로 표현하면
lcs[i-1][j-1] +1 이렇게 나타난다.

결국 최장 공통 부분 수열을 lcs[a의 길이][b의 길이]에 저장된다.

public class Main {
    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));

        char input1[] = br.readLine().toCharArray();
        char input2[] = br.readLine().toCharArray();

        int len1 = input1.length;
        int len2 = input2.length;

        int lcs[][] = new int[len1+1][len2+1];

        lcs[0][0] = 0;
        for (int i = 1; i <= len1; i++) {
            for (int j = 1; j <= len2; j++) {
                if (input1[i-1] == input2[j-1]) lcs[i][j] = lcs[i-1][j-1] + 1;
                else
                    lcs[i][j] = Math.max(lcs[i][j-1], lcs[i-1][j]);
            }
        }

        System.out.println(lcs[len1][len2]);


    }
}

[출처] : https://velog.io/@emplam27
https://st-lab.tistory.com/139