[백준/C++] 11052번_카드 구매하기

문제는 다음과 같습니다.

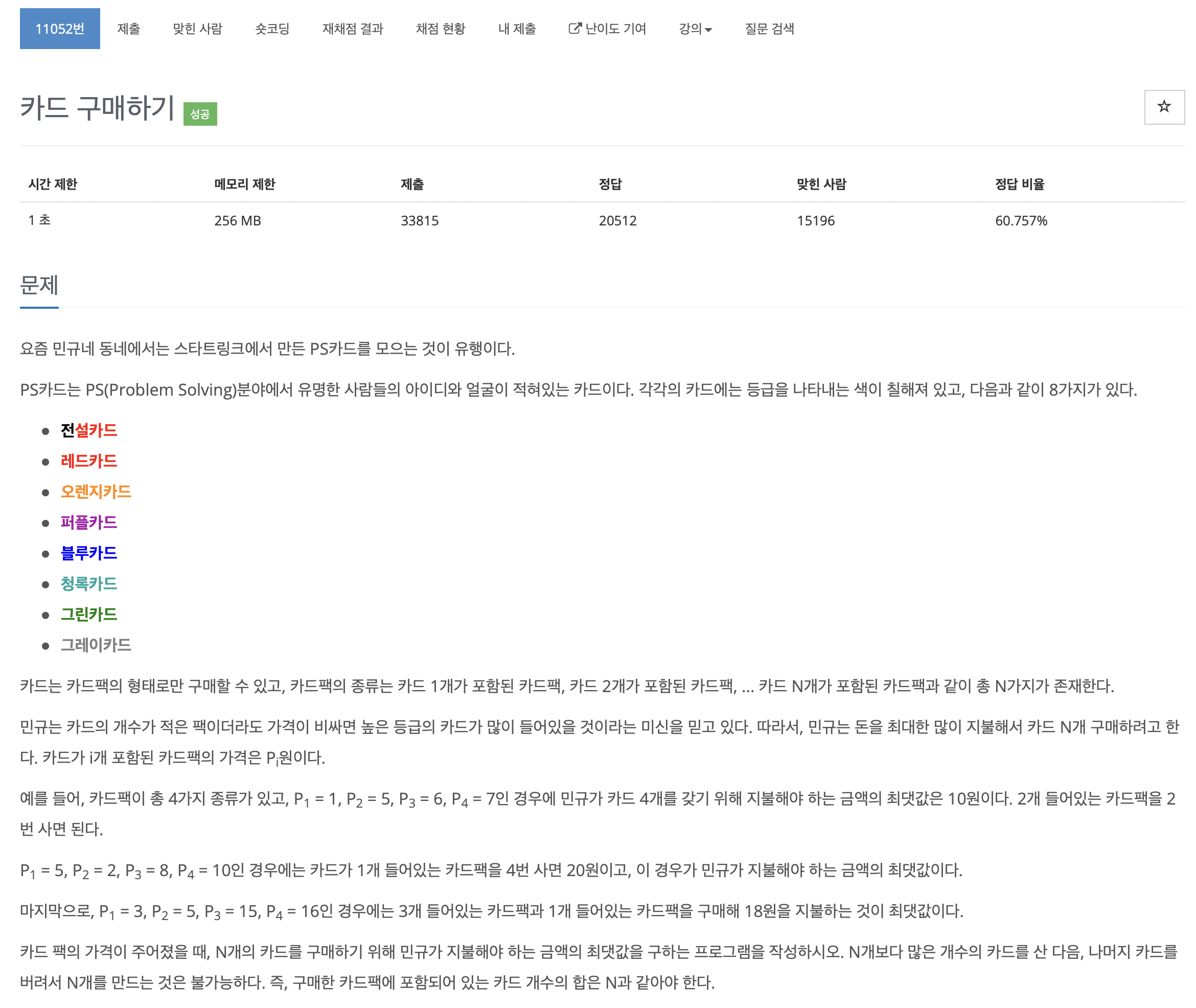
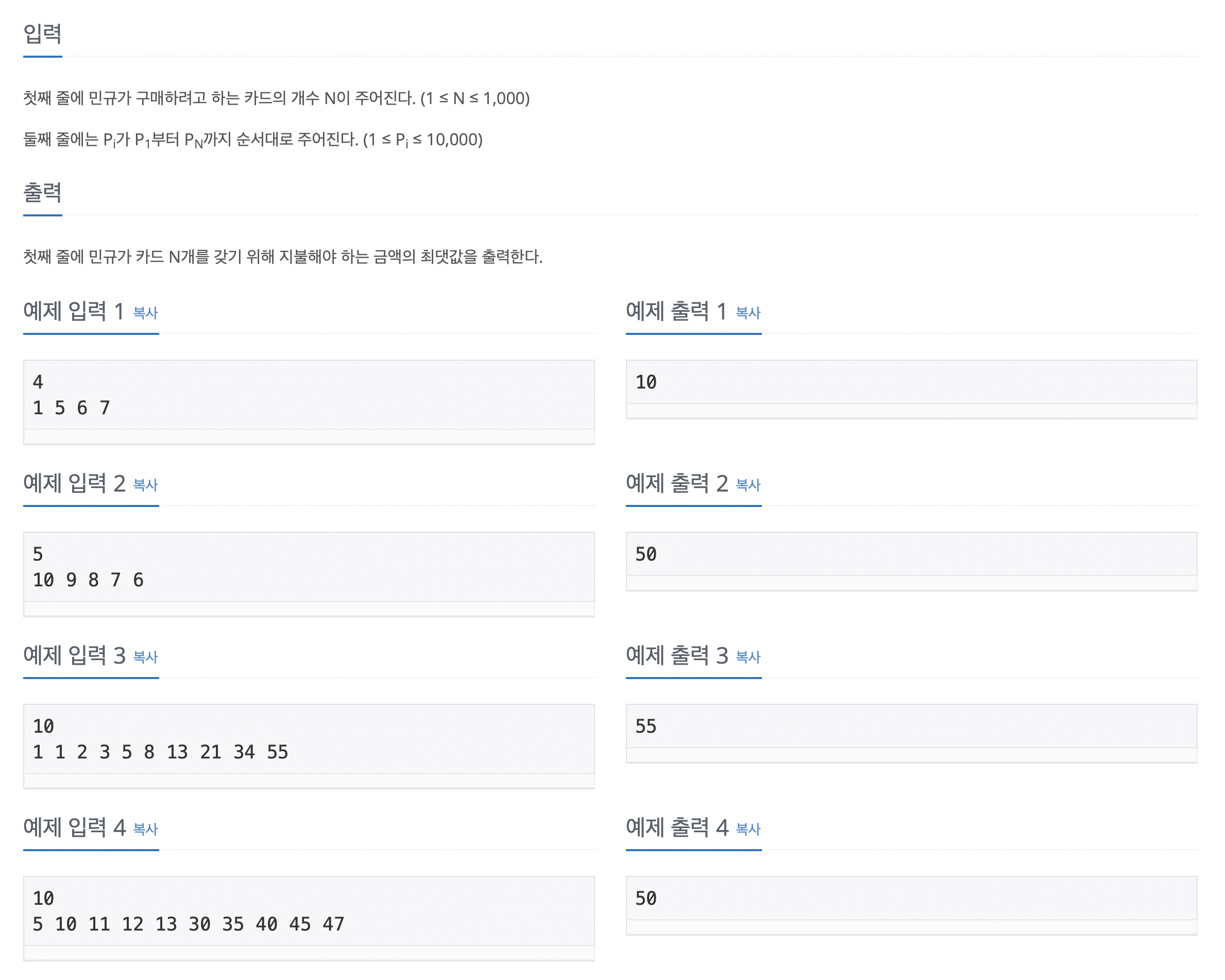
카드팩에 들어있는 카드의 개수에 따라 금액이 달라지기 때문에, 일단 메모이제이션을 이용해야겠다는 생각을 했구요

그리고 생각을 한 것이,
4 숫자를 1~4를 이용해서 어떻게 만들 수 있는가.

이를 생각해보면 다음과 같습니다.
4 < 4(4)의 조합 >
3 1 < 3(3)과 1(1)의 조합 >
2 2 < 2(2)와 2(2)의 조합 >
2 1 1 < 2(2)와 2(1, 1)의 조합 >
1 1 1 1 < 2(1, 1)와 2(1, 1)의 조합 >

그래서 배열 d[n]에는 카드 n개를 갖기 위해 지불해야 하는 금액의 최댓값을 저장을 하고,
d[n]을 구하기 위해서는
먼저 n개를 지불하는 값을 최대로 지정한 후,

1부터 ~ n-1까지 대칭적으로 구한 합과 최대를 슬라이딩윈도우로 현재의 최댓값과 비교 후에 계속해서 갱신해나가면 됩니다.
이는 대칭이기에, 대칭의 절반(n/2)까지만 진행하면 됩니다.

핵심 과정은 다음과 같습니다.

      d[i]=tmp;
      for(int j=i-1; j>=i/2; j--){
        d[i]=max(d[i], d[j]+d[i-j]);
      }

전제 코드는 다음과 같습니다.

#include <bits/stdc++.h>
using namespace std;

int d[1001]={0, };

int main() {
    ios_base::sync_with_stdio(false);
    cin.tie(nullptr);

    int n, tmp, res, cnt=0;
    cin>>n;
    cin>>tmp;
    d[1]=tmp;

    for(int i=2; i<=n; i++){
      cin>>tmp;
      d[i]=tmp;
      for(int j=i-1; j>=i/2; j--){
        d[i]=max(d[i], d[j]+d[i-j]);
      }
    }

    cout<<d[n]<<endl;
    
    return 0;
}

---

2/5 토요일 복습)

#include <bits/stdc++.h>
using namespace std;

int main() {
    ios_base::sync_with_stdio(false);
    cin.tie(nullptr);

    int dp[1001]={0, };
    int n, tmp; cin>>n;
    for(int i=1; i<=n; i++){
      cin>>tmp;
      dp[i]=tmp;
    }

    for(int i=2; i<=n; i++){
      for(int j=i-1; j>=1; j--){
        dp[i]=max(dp[i], dp[i-j]+dp[j]);
      }
    }

    cout<<dp[n]<<endl;
    return 0;
}

그리고 추가로 가져온 풀이가 있는데,
이 방법은 입력받은 Pi (1<=i<=n)에 대해서 배열 a에 따로 저장을 해주고 계산하였습니다.

#include <bits/stdc++.h>
using namespace std;

int main() {
    ios_base::sync_with_stdio(false);
    cin.tie(nullptr);

    int dp[1001]={0, };
    int a[1001]={0, };
    int n, tmp; cin>>n;
    for(int i=1; i<=n; i++){
      cin>>tmp;
      a[i]=tmp;
    }

    for(int i=1; i<=n; i++){
      for(int j=i; j>=1; j--){
        dp[i]=max(dp[i], dp[i-j]+a[j]);
      }
    }

    cout<<dp[n]<<endl;
    return 0;
}

여기서는 dp[i]가 n이하인 경우를 생각해주어야하기 때문에, j가 i부터 시작해야합니다.😊

모든 풀이의 시간복잡도는 O(n^2)입니다.