[백준/C++] 1912번_연속합

문제는 다음과 같습니다.

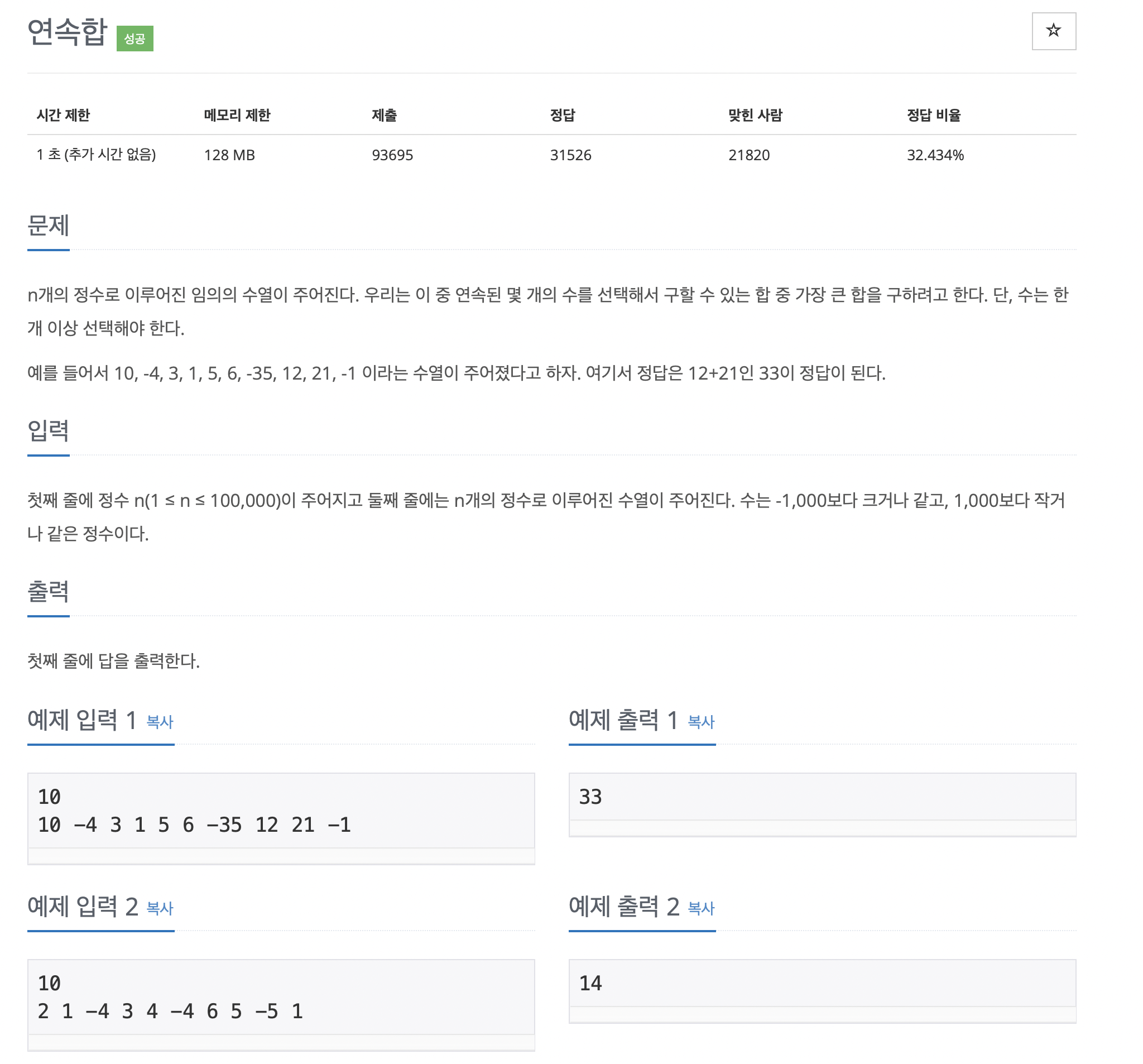
먼저 제가 생각한 방법은 다음과 같습니다.
전역배열 a[n]에 대해서,
이는 n번째 항을 포함했을때 얻을 수 있는 부분수열의 최댓값을 저장을 합니다.
즉, n번째 항은 반드시 포함이라는 의미입니다.

a[n]을 귀납법으로 생각해보았을 때,
a[n]은 두 가지 경우가 나올 수 있고, a[n]에는 두 가지 경우 중 최댓값을 저장하면 됩니다.

• 경우1: a[n-1]을 포함한 경우
• 경우2: a[n-1]을 포함하지 않은 경우

즉, 이를 다음과 같이 나타낼 수 있습니다.

a[n] = max(a[n-1] + n번째 항, n번째 항)

그리고 연속된 합의 최대는 배열 a[n]에 들어있는 값들 중 최댓값을 구하면 됩니다.
이를 res 변수에 계속해서 갱신해주었습니다.

전체 코드는 다음과 같습니다.

#include <bits/stdc++.h>
using namespace std;

int a[100001]={0, };

int main() {
    ios_base::sync_with_stdio(false);
    cin.tie(nullptr);

    int n, tmp, res;
    cin>>n;
    cin>>tmp;
    a[1]=tmp;
    res=a[1];

    for(int i=2; i<=n; i++){
      cin>>tmp;
      a[i]=max(a[i-1]+tmp, tmp);
      res=max(res, a[i]);
    }

    cout<<res<<endl;
    
    return 0;
}

대부분의 다른 풀이가 비슷해서, 다른 풀이는 생략하도록 하겠습니다.

2월 8일 화요일 복습)

#include <bits/stdc++.h>
using namespace std;

int main() {
    ios_base::sync_with_stdio(false);
    cin.tie(nullptr);
    
    long long dp[100001]={0, };
    long long res, tmp, n; cin>>n;
    cin>>tmp; res=tmp; dp[0]=tmp;

    for(int i=1; i<n; i++){
      cin>>tmp;
      dp[i]=max(tmp, dp[i-1]+tmp);
      res=max(res, dp[i]);
    }
    cout<<res<<"\n";
    return 0;
}