미분 (differentiation)

• 변수의 움직임에 따른 함수값의 변화를 측정하기 위한 도구
• 최적화에서 제일 많이 사용하는 기법
• 변화율의 극한(limit)으로 정의

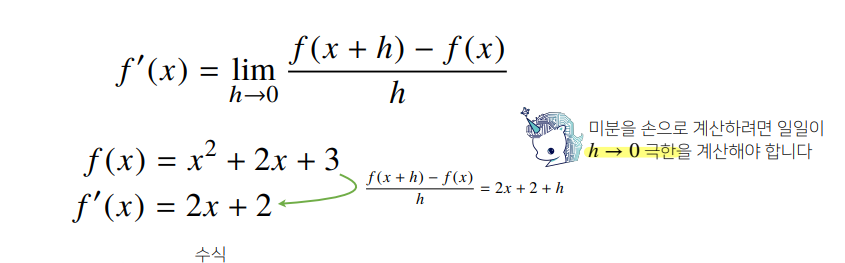
• sympy.diff 를 통한 미분 계산
  
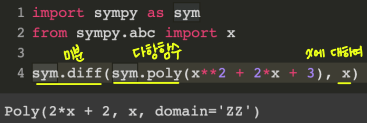
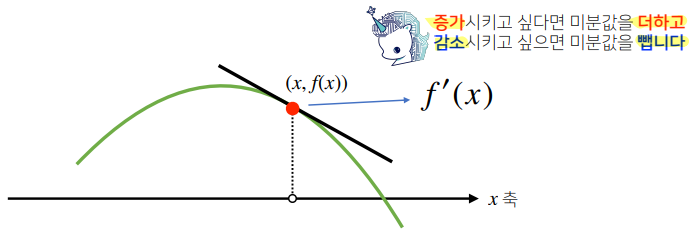
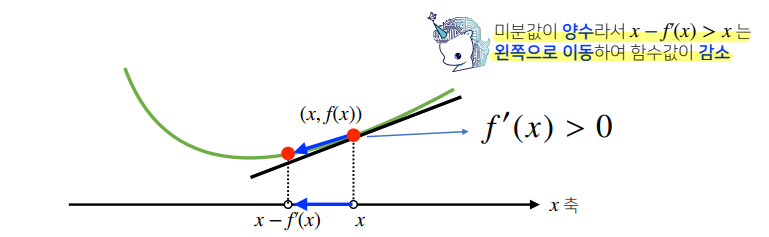
• 미분은 함수 $f$의 주어진 점 $(x, f(x))$에서의 접선의 기울기를 구한다.
  
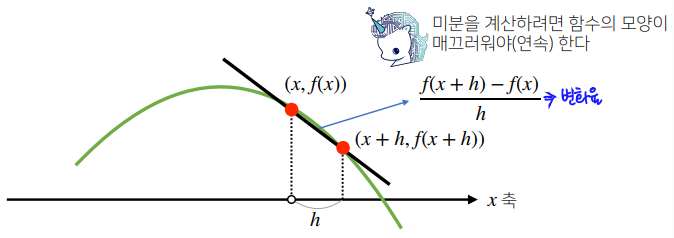
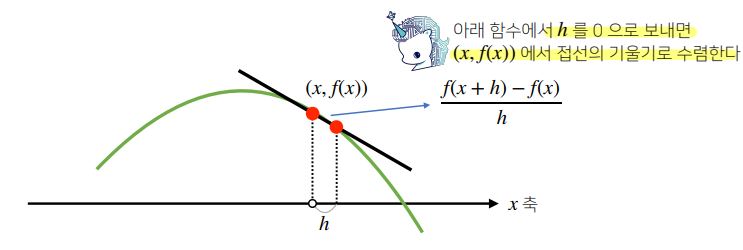
• 한 점에서 접선의 기울기를 알면 어느 방향으로 점을 움직여야 함수값이 증가/감소하는지 알 수 있다.

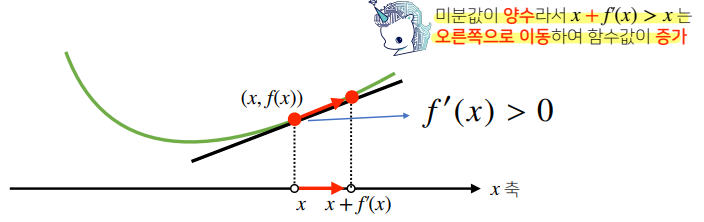
경사상승법(grdient ascent)

미분값을 더해 함수의 극대값의 위치를 구하는 것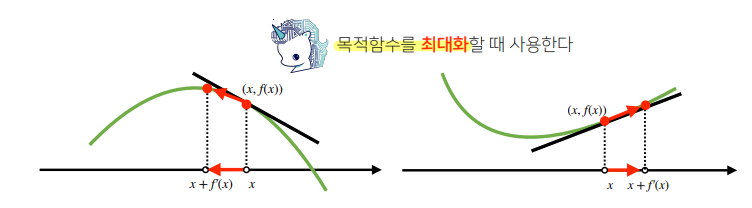

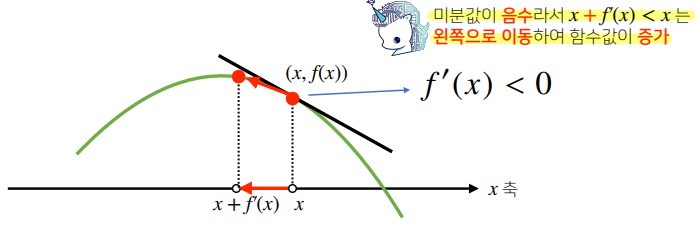
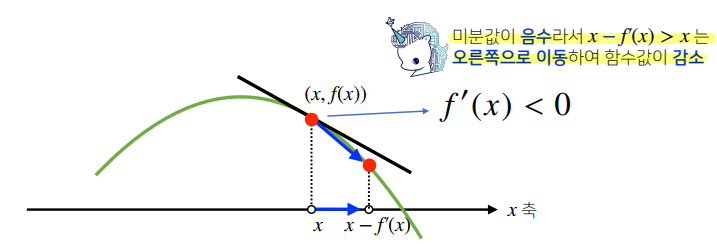
경사하강법(grdient descent)

미분값을 빼서 함수의 극소값의 위치를 구하는 것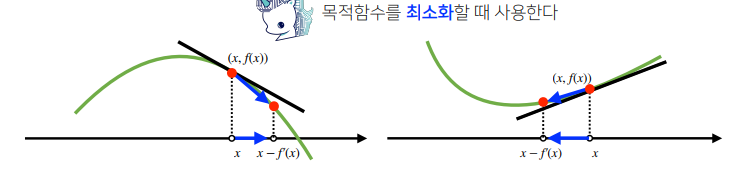

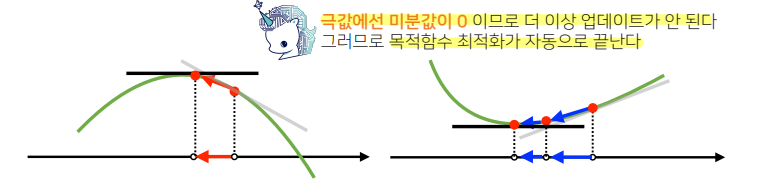
• 경사상승 / 경사하강방법은 극값에 도달하면 움직임(업데이트, 목적함수 최적화)을 멈춘다.

알고리즘

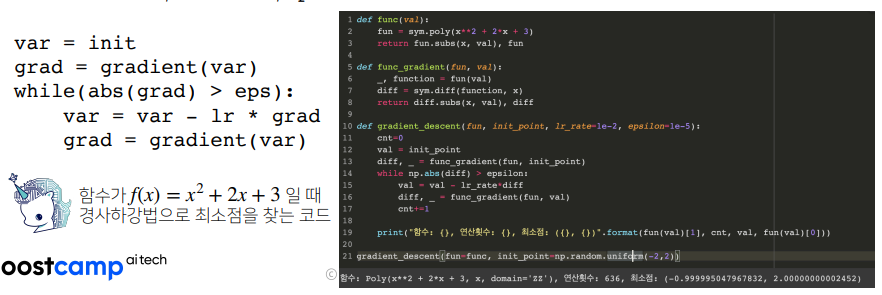
만약 벡터가 입력 변수인 다변수 함수의 경우 편미분을 사용한다.

편미분(partial differentiation)

• 이 때 벡터 차원(=구성성분 수)에 따라 각 변수 별로 편미분을 계산한 그레디언트 벡터(gradient vector)를 이용해 경사하강/경사상승법에 사용한다.

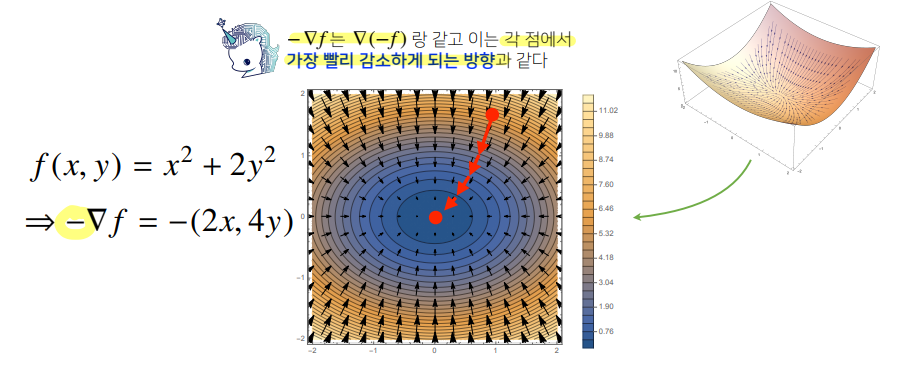
그레디언트 벡터 (gradient vector)

• $d$차원 공간에서 $d$개의 원소를 가진 벡터를 편미분한 것
• 기호 : $\nabla$ ($nabla$)
  
• $\nabla$$f$
• $-\nabla$$f$ $=\nabla(-f)$

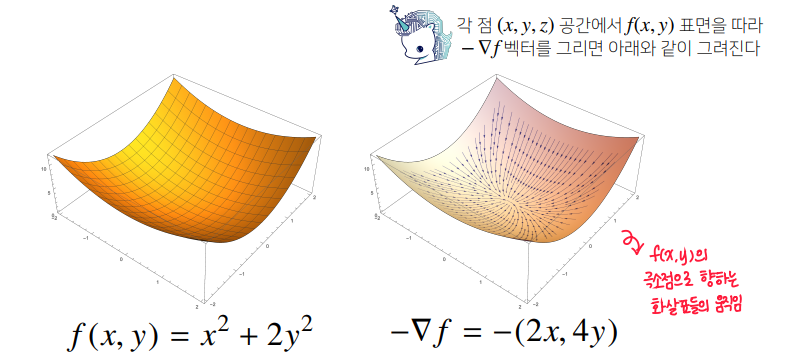
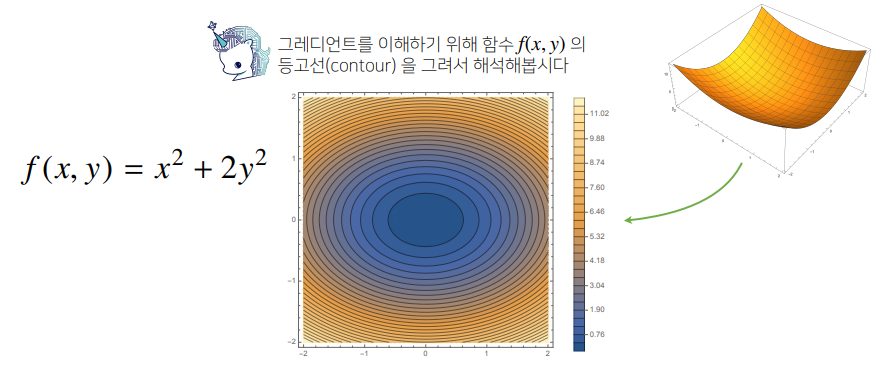
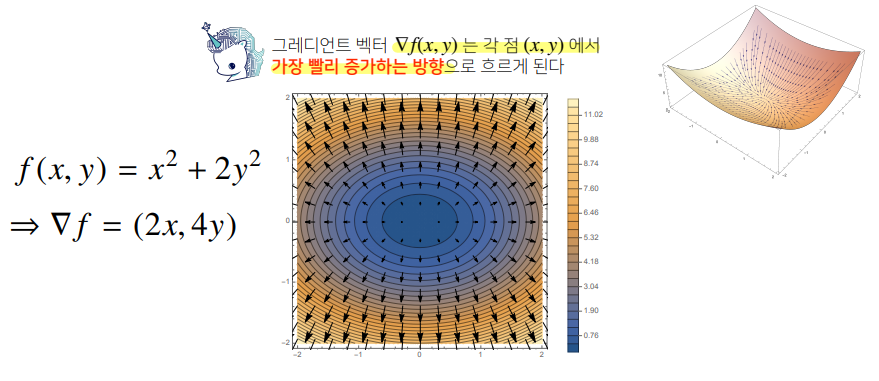
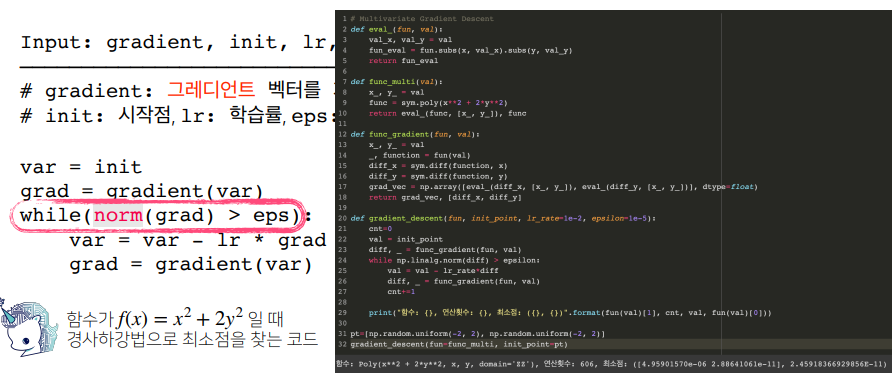
알고리즘

그레디언트 벡터는 절대값 대신 노름(norm)을 계산해서 종료조건을 설정한다.

---

review

• 미분 (differentiation)
  • sympy.diff
  • 경사상승법
  • 경사하강법
  • 알고리즘
    • gradient
    • init
    • lr
    • eps
• 편미분(partial differentiation)
  • 벡터의 미분
  • 그레디언트 벡터(gradient vector)
  • 알고리즘
    • 노름(norm)
    • gradient
    • init
    • lr
    • eps