학습 목표

• 선형회귀모델을 이해합니다.
• 지도학습(Supervised Learning)을 이해합니다.
• 회귀모델에 기준모델을 설정할 수 있습니다.
• Scikit-learn을 이용해 선형 회귀 모델을 만들어 사용하고 해석할 수 있습니다.

---

지도학습(Supervised Learning)

• 입력과 출력 샘플 데이터가 있고, 주어진 입력으로부터 출력을 예측하고자 할 때 사용
• 이미 알려진 사례를 바탕으로 일반화된 모델을 만들어 의사 결정 프로세스를 자동화하는 것
• 사용자가 알고리즘에 입력과 기대되는 출력(레이블이 있는 데이터)을 제공하고 알고리즘은 주어진 입력에서 원하는 출력을 만드는 방법을 찾아 새로운 입력이 주어질 때 적절한 출력을 만들 수 있게 된다.
  
  

분류(classification)

미리 정의된, 가능성 있는 여러 클래스 레이블 중 하나를 예측하는 것

• 이진 분류 : 두 개의 클래스로 분류(예/아니오)
• 다중 분류 : 셋 이상의 클래스로 분류
  
  

회귀(regression)

• 연속적인 숫자, 또는 프로그래밍 용어로 말해 부동소수점수(수학 용어로는 실수)를 예측하는 것
• 특정 변수(독립 변수)가 다른 변수(종속 변수)에 어떠한 영향을 미치는가를 분석하는 지도 학습 방법
• 인과 관계가 있는지 등을 분석하기 위한 방법으로 변수 1개 이상의 값을 가지고 다른 변수의 값을 예측해주는 분석 방법
  
  
  

---

선형회귀(linear regression), 최소제곱법(OLS, ordinary least squares)

• 관찰된 데이터들을 기반으로 하나의 함수를 구해서 관찰되지 않은 데이터의 값을 예측하는 것
• 회귀 계수들이 선형 결합(linear combination)된 함수
  
  
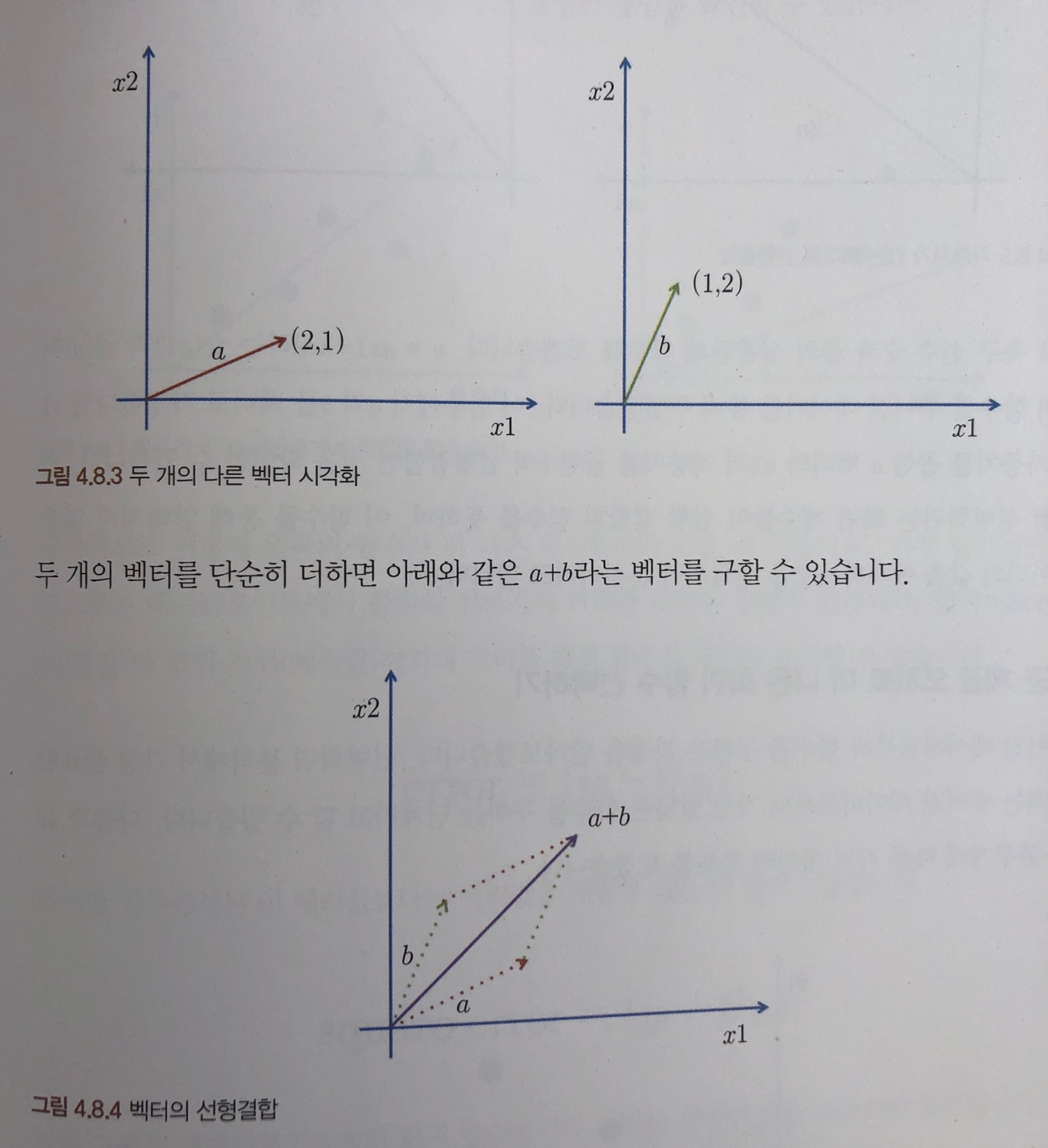
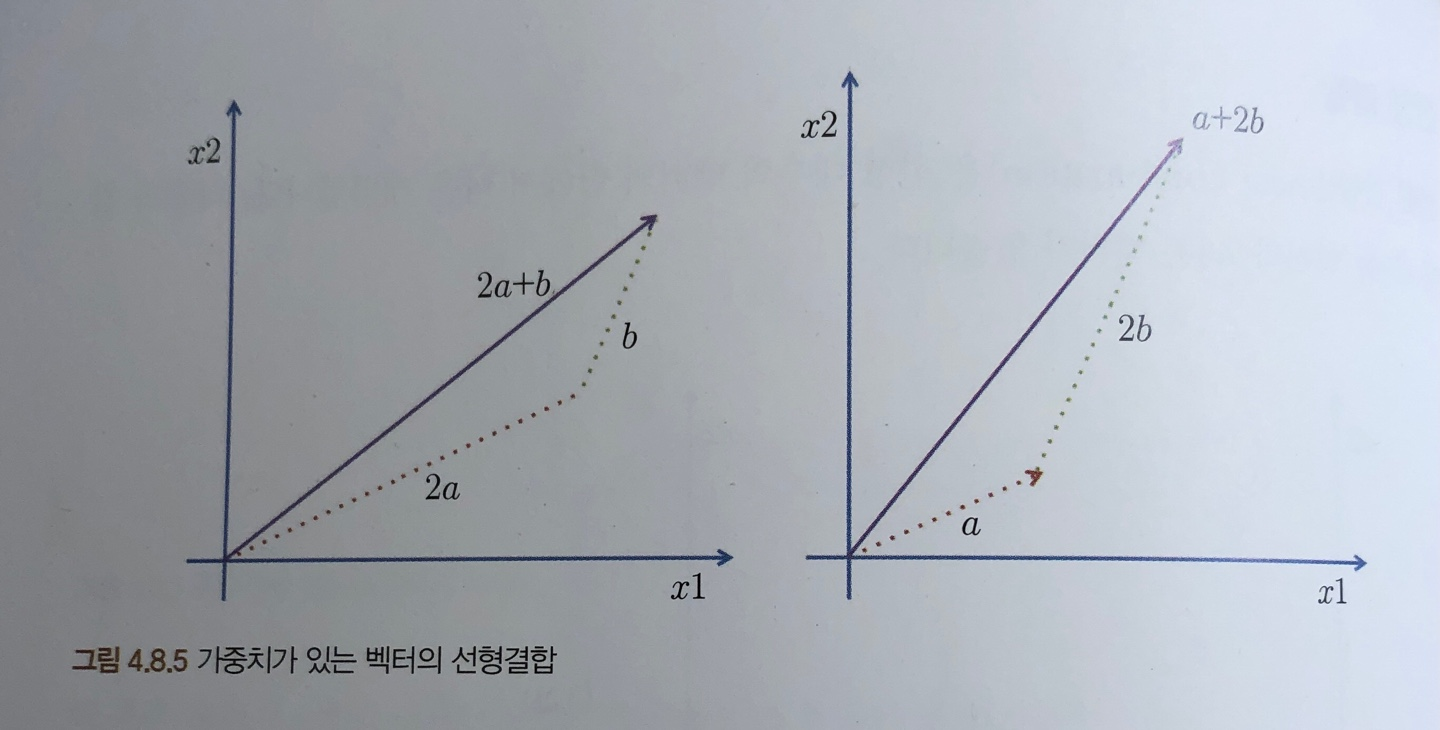
• 종속변수 y와 한 개 이상의 독립변수 x와의 선형 상관관계를 요약 및 모델링하는 회귀분석 기법

  • 종속변수 : 반응(Response)변수, 레이블(Label), 타겟(Target)등
  • 독립변수 : 예측(Predictor)변수, 설명(Explanatory), 특성(feature) 등

• 지도학습 중 연속 값 예측 문제에 사용하는 모델(예측 문제 : 기존 데이터를 기반으로 생성된 모델을 이용하여 새로운 데이터가 들어왔을 때 어떤 값이 될지 예측하는 문제)
• 계수를 쉽고 직관적으로 확인할 수 있으며 한 feature의 단위가 커질수록 target이 얼마나 변하는지, 어떻게 변하는지 직관적으로 확인할 수 있는 점이 특징입니다.
• 회귀식을 찾는 것이 목적(*회귀식 : 학습을 통해 찾는 회귀선을 함수로 표현한 식 )
• 회귀식을 통해 실제 주어져 있지 않은 점의 함수값 보간(interpolate) &기존 데이터의 범위를 넘어서는 값을 예측하기 위한 외삽(extrapolate) 제공
  
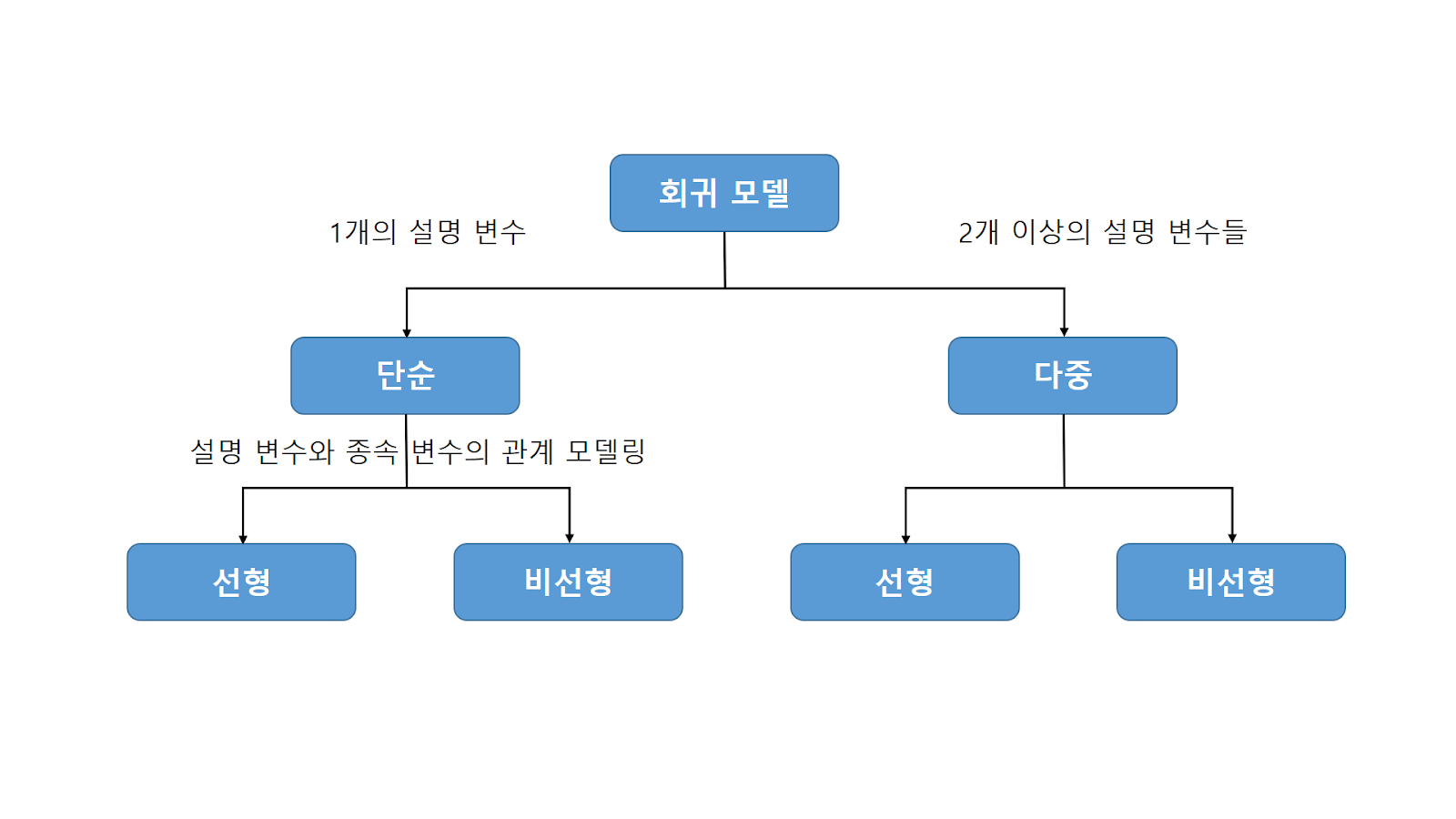
• 단순 선형회귀(Simple Linear Regression) : 1개의 설명 변수에 기반
• 다중 선형회귀(multiple-regression) : 2개 이상의 설명 변수에 기반
  
  

회귀 직선 관련 중요 개념

• 예측값 : 모델이 추정하는 값
• 잔차 : 예측값과 관측값 차이 in 표본집단(≠오차: in 모집단)
• 회귀선 : 잔차 제곱들의 합인 RSS(Residual Sum of Squares)를 최소화 하는 직선
• RSS : 회귀모델의 비용함수(Cost function), SSE(Sum of Square Error)라고도 불림
  ${\displaystyle \operatorname {RSS} =\sum _{i=1}^{n}(\varepsilon _{i})^{2}=\sum _{i=1}^{n}(y_{i}-f(x_{i}))^{2}=\sum _{i=1}^{n}(y_{i}-(\alpha x_{i} + \beta))^{2}}$
• MSE(Mean squared error) : 평균 제곱 오차
  -> 빨간 사각형들의 평균값이 작은 함수가 더 나은 회귀 함수
• α, β : RSS를 최소화 하는 값으로 모델 학습을 통해서 얻어지는 값
• 최소제곱회귀 or Ordinary least squares(OLS) : 잔차제곱합을 최소화하는 방법
  $\beta =\displaystyle {\bar {y}}-\alpha{\bar {x}}$,
  $\alpha ={\frac {S_{xy}}{S_{xx}}}$
  ${\displaystyle S_{xy}=\sum _{i=1}^{n}(x_{i}-{\bar {x}})(y_{i}-{\bar {y}})}$, ${\displaystyle S_{xx}=\sum _{i=1}^{n}(x_{i}-{\bar {x}})^{2}}$
  수학산책-최소제곱법
• 학습 : 비용함수를 최소화하는 모델을 찾는 과정

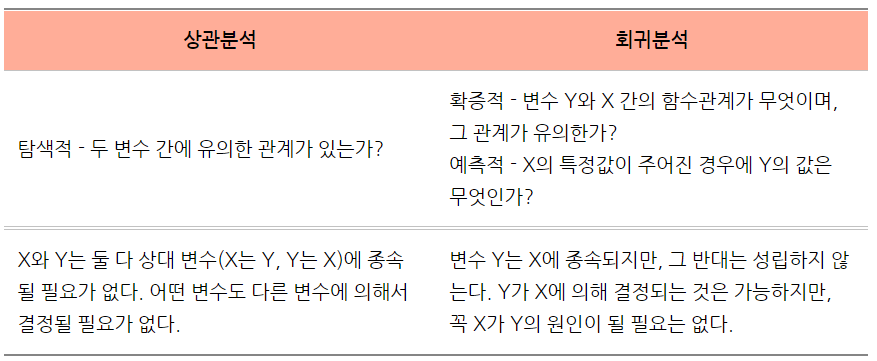
*선형 상관분석(Linear correlation) vs 선형 회귀분석(Linear regression)
상관분석은 두 변수의 값이 유의한 관계가 있는지, 즉 두 변수 값이 일관성을 갖고 변화하는지를 검토하기 위한 탐색적인 방법이다. (예를 들어, 한 변수 값이 증가함에 따라 다른 변수 값이 감소하는 경우) 그래서 하나의 변수 값을 다른 변수의 값으로부터 예측할 수 있다거나 그 변수들 간에 어떤 인과관계가 있는지를 보는 것에 대해서는 기대할 수 없다.

반대로, 회귀분석은 두 변수들 간의 함수관계를 설명하는데 사용되므로 하나의 변수 값으로부터 다른 변수 값을 예측할 수 있다. 함수관계는 종속변수(dependent variable)가 독립변수(independent variable)에 의해 결정이 될 수 있지만, 그 반대는 성립하지 않는 것을 의미한다. 종속변수가 독립변수에 의해 결정될 수 있지만 독립변수가 꼭 종속변수의 직접적인 원인이 될 필요가 없다는 가설에 대한 타당한 근거가 있는 경우에 회귀분석을 사용할 수 있다.(다른 원인이 있을 수도 있다라는 가정)

선형회귀모델링 프로세스

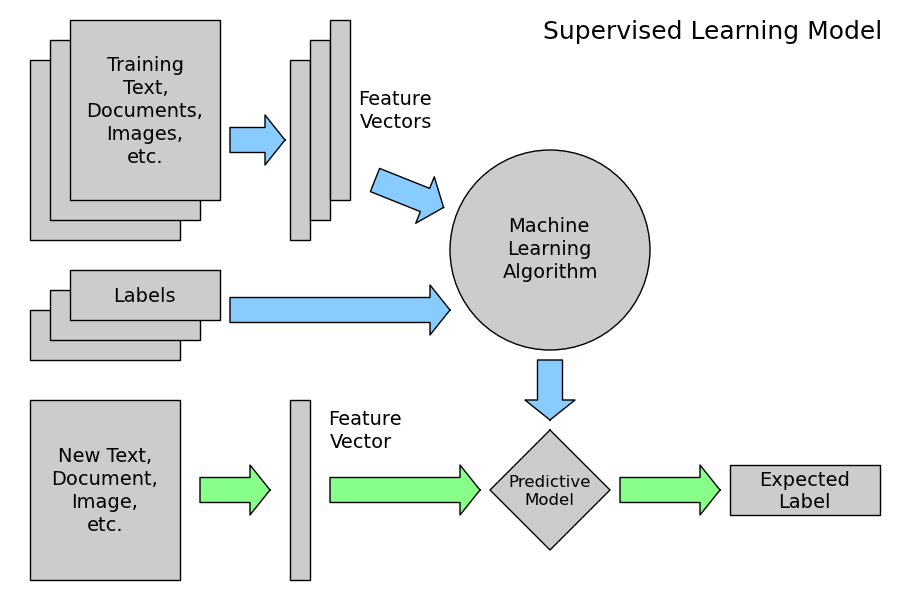
0. 풀어야 하는 문제를 풀기에 적합한 모델을 선택하여 클래스를 찾아본 후 관련 속성이나 하이퍼파라미터 확인

1. 데이터 준비 후 기존 경험을 바탕으로 예측

한마디로 대충 어림짐작하는 것 입니다. 예를 들어 밤 하늘에 달무리가 진 것을 보고 다음날 날씨가 흐릴 것을 예측하는 것과 같습니다. 보통 좋은 결과를 내기도 하지만 사람마다 편견이 존재하며 오류에 빠질 위험이 높습니다.

2. 통계정보 활용

# pandas 포멧팅을 사용하면, 판다스 객체들의 결과에서 쉼표를 넣고 소숫점 아래는 생략하도록 설정할 수 있습니다.
# float 형식 소숫점 1자리, 쉼표 포함
pd.set_option('display.float_format', '{:,.1f}'.format)

# 기본 셋팅으로 돌아오기 위해서
# pd.set_option('display.float_format', None) 


df['SalePrice'].describe()


##시각화
import matplotlib.pyplot as plt
import seaborn as sns

## SalePrice의 확률밀도함수
sns.displot(df['SalePrice'], kde=True)

## 평균과, 중간값으로 수직선 그리기
plt.axvline(df['SalePrice'].mean(), color='blue')
plt.axvline(df['SalePrice'].median(), color='red');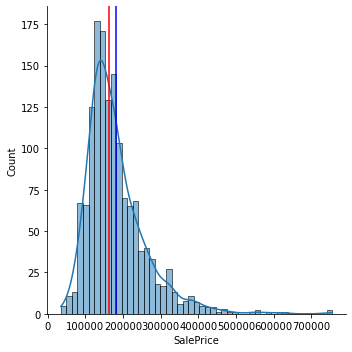

3. 기준모델(Baseline Model)

예측 모델을 구체적으로 만들기 전에 가장 간단하면서도 직관적이면서 최소한의 성능을 나타내는 기준이 되는 모델로 최소한의 기준을 만들어 내가 만든 모델과 비교하기 위해 필요합니다.

문제별로 기준모델은 보통 다음과 같이 설정합니다.

• 분류문제: 타겟의 최빈 클래스
• 회귀문제: 타겟의 mean, median
• 시계열회귀문제: 이전 타임스탬프의 값(직전 시간의 데이터)

## predict: 우리가 정한 기준모델인 평균으로 예측을 합니다
predict = df['SalePrice'].mean()

## 평균값으로 예측할 때 샘플 별 평균값과의 차이(error)를 저장합니다
errors = predict - df['SalePrice']

## mean_absolute_error(MAE), 예측 error 의 절대값 평균
mean_absolute_error = errors.abs().mean()

##단순선형회귀 그래프_회귀선
x = df['GrLivArea']
y = df['SalePrice']

predict = df['SalePrice'].mean()
errors = predict - df['SalePrice']
mean_absolute_error = errors.abs().mean()

sns.lineplot(x=x, y=predict, color='red')
sns.scatterplot(x=x, y=y, color='blue');

print(f'예측한 주택 가격이 ${predict:,.0f}이며 절대평균에러가 ${mean_absolute_error:,.0f}임을 확인할 수 있습니다.')

-> 평균 예측은 에러가 상당히 크다는 것을 알 수 있습니다.

변수(특성) 간의 상관관계(dependent)

1. df.corrwith(한 변수&나머지 모든 변수), df.corr(상관계수)
그룹 별 변수 간 상관관계 분석 (correlation with columns by groups)

2. 시각화

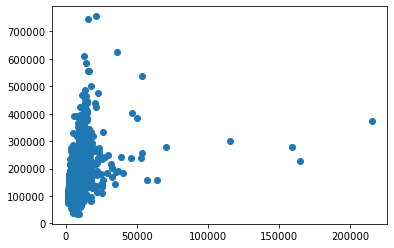
## 1개 독립변수
plt.scatter(df['LotArea'], df['SalePrice']);

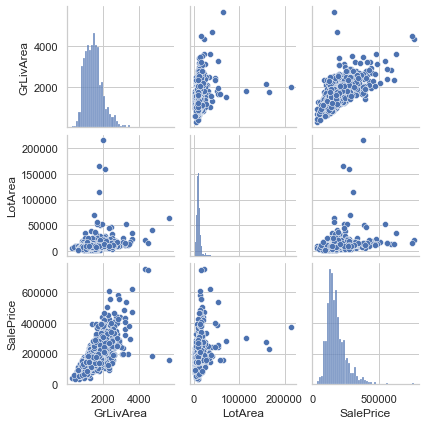
## 2개 독립변수
sns.set(style='whitegrid', context='notebook')
cols = ['GrLivArea', 'LotArea','SalePrice']
sns.pairplot(df[cols], height=2);

4. 예측모델(Predictive Model) 활용

• 회귀 예측 모델 = 데이터 scatterplot에 가장 잘 맞는(best fit) 직선
• fit() : 모델 학습, predict() : 새로운 데이터 예측
• scatterplot

  특성&타겟
  

  • 특성행렬 : 주로 X 로 표현하고 보통 2-차원 행렬입니다([n_samples, n_features]). 주로 NumPy 행령이나 Pandas 데이터프레임으로 표현합니다.
  • 타겟배열 : 주로 y로 표현하고 보통 1차원 형태(n_samples) 입니다. 주로 Numpy 배열이나 Pandas Series로 표현합니다.

학습 및 예측

from sklearn.linear_model import LinearRegression

# X 특성들의 테이블과, y 타겟 백터 생성
feature = ['내가 사용할 특성']
target = ['타겟']
X_train = df[feature]
y_train = df[target]

# 모델 학습(fit)
model = LinearRegression().fit(X_train, y_train)

# 만들어진 model로 test data 예측(predict)
X_test = [[x] for x in df_t['GrLivArea']]
y_pred = model.predict(X_test)      # X_test로 수행

# train & test data graph
plt.scatter(X_train, y_train, color='black', linewidth=1)
plt.scatter(X_test, y_pred, color='blue', linewidth=1)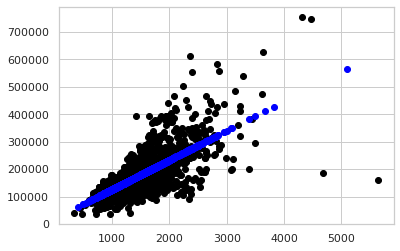

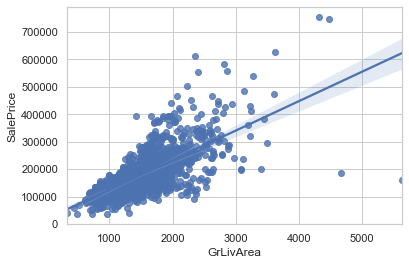
단순선형회귀 적합선/모델 시각화
Show plot data and a linear regression model fit.

import seaborn as sns
sns.regplot(x=df['GrLivArea'], y=df['SalePrice'])
# fit_reg=False -> no regression line

선형회귀모델의 계수(Coefficients)와 절편(intercept)

## 계수(coefficient)_기울기
model.coef_

## 절편(intercept)
model.intercept_

• Using Interact

from ipywidgets import interact

# 데코레이터 interact를 추가합니다.
@interact
def explain_prediction(sqft=(500,10000)):
    y_pred = model.predict([[sqft]])
    pred = f"{int(sqft)} sqft 주택 가격 예측: ${int(y_pred[0])} (1 sqft당 추가금: ${int(model.coef_[0])})"

    return pred

예제

## Scikit-Learn 라이브러리에서 사용할 예측모델 클래스를 Import 
from sklearn.linear_model import LinearRegression


## 예측모델 인스턴스
model = LinearRegression()


## X 특성들의 테이블, y 타겟 벡터
feature = ['GrLivArea']
target = ['SalePrice']
X_train = df[feature]
y_train = df[target]


## 모델을 학습(fit)
model.fit(X_train, y_train)


## 새로운 데이터 한 샘플을 선택해 학습한 모델을 통해 예측
X_test = [[4000]]
y_pred = model.predict(X_test)

print(f'{X_test[0][0]} sqft GrLivArea를 가지는 주택의 예상 가격은 ${int(y_pred)} 입니다.')
>>> 4000 sqft GrLivArea를 가지는 주택의 예상 가격은 $447090 입니다.


## 전체 테스트 데이터를 모델을 통해 예측
X_test = [[x] for x in df_t['GrLivArea']]
y_pred = model.predict(X_test)


## 전체 예측값 
y_pred
>>> array([[114557.82748987],
       [160945.27292207],
       [193084.38061182],
       ...,
       [149696.58523066],
       [122485.47405334],
       [232829.74378814]])
       
       
## train 데이터에 대한 그래프를 그려보겠습니다.
plt.scatter(X_train, y_train, color='black', linewidth=1)

## test 데이터에 대한 예측을 파란색 점으로 나타내 보겠습니다.
plt.scatter(X_test, y_pred, color='blue', linewidth=1);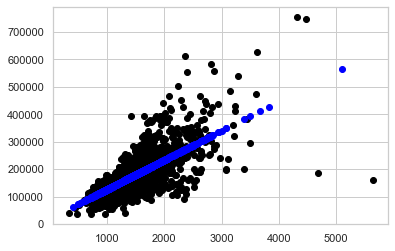

데이터를 입력하고 어떤 룰에 따라 답을 구해내는 일반적인 프로그래밍과 달리 머신러닝은 데이터와 답을 통해 룰을 찾아내는 방법이라고 볼 수 있습니다.
a new programming paradigm

[reference]

선형회귀(Linear Regression)
[선형회귀] 나 다시 돌아갈래, 선형회귀 Overview