데이터 나누기
회귀모델을 만들기 전에 모델의 성능을 평가하기 위해
훈련(train)과 테스트(test) 데이터로 나눈다
훈련데이터를 사용해서 학습을 하여 모델을 만들고 학습에 사용하지 않은 테스트데이터를 얼마나 잘 맞추는지가 중요
(나누는 이유 : 나눠야 모델의 예측 성능을 제대로 평가할 수 있다)
⚠️ 학습에 사용하는 데이터와 모델을 평가하는데 사용하는 데이터는 달라야한다
※ 데이터를 무작위로 선택해 나누는 방법이 일반적, 시계열 데이터는 훈련데이터보다 테스트 데이터가 미래의 것이어야 한다
다중선형회귀모델(특성 2개 이상)
# 훈련 / 테스트 데이터로 나누기
train = df.sample(frac = 0.8, random_state=1)
test = df.drop(train.index)
features = ['AAAA', 'BBBB'] # 특성 2개
target = ['TTTT']
X_train = train[features]
X_test = test[features]
y_train = train[target]
y_test = test[target]
model = LinearRegression()
model.fit(X_train, y_train) # 모델 학습
y_pred = model.predict(X_train) # 모델 예측
model.intercept_ # 절편값 출력 -102743
model.coef_ # 계수 출력 array([54.401, 33059.442)
# 회귀식 y = -102743 + 54x₁ + 33059x₂ 장점 : 선형회귀는 다른 머신러닝 모델에 비해 상대적으로 학습이 빠르고 설명력이 강하다
단점 : 선형모델이므로 과소적합(underfitting)이 잘 일어난다
과적합(Overfitting) / 과소적합(Underfitting)
일반화 오차 : 테스트 데이터에서 만들어내는 오차
모델이 너무 훈련데이터에 과하게 학습(과적합)을 하지 않도록 하는 일반화 방법이 있다
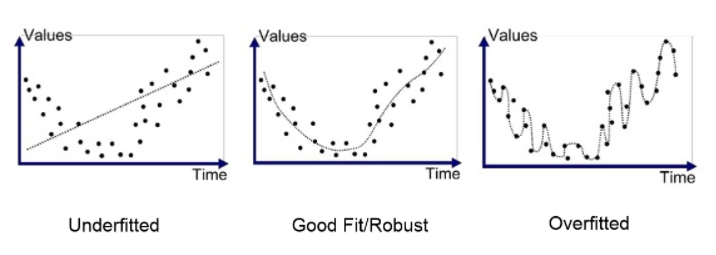
- 과적합 : 모델이 훈련데이터에만 특수한 성질을 과하게 학습해 일반화를 못해 결국 테스트데이터에서 오차가 커지는 현상
- 과소적합 : 훈련데이터에 과적합도 못하고 일반화 성질도 학습하지 못해 훈련/테스트 데이터 모두에서 오차가 크게 나오는 경우
ex) 과소적합 / 과적합 예시
분산 / 편향 트레이드오프
과/소적합은 오차의 편향(Bias)과 분산(Variance) 개념과 관계가 있다
- 분산이 높은 경우는 모델이 학습 데이터의 노이즈에 민감하게 적합하여 테스트데이터에서 일반화를 잘 못하는 경우 과적합 상태이다
- 편향이 높은 경우는 모델이 학습데이터에서 특성과 타겟 변수의 관계를 잘 파악하지 못해 과소적합 상태이다
선형모델 예측은 학습데이터에서 타겟값과 오차가 크다 - 편향이 높다(과소적합)
훈련/테스트 두 데이터에서 그 오차가 비슷하다 - 분산이 낮다

곡선을 피팅한 모델에서는 학습데이터에서 오차가 0에 가깝지만 테스트 데이터에서 오차가 많아진다
분산(Bias) / 편향(Variance)

※ 낮은 분산에 낮은 편향을 가져야 좋은 모델이다
모델의 복잡성에 따른 성능 그래프

※ 모델의 복잡성에 따라 성능 그래프를 그려 보면 모델이 복잡해질수록 훈련데이터 성능은 계속 증가하지만 검증데이터 성능은 어느정도 증가하다가 오히려 낮아지는 지점이 생긴다 → 이 시점이 과적합이 일어나는 시점