우선 mode가 무엇인지 이야기해보자.
모드는 통계학에서 자주 쓰이는 용어로 한 데이터 집합에서 가장 자주 등장하는 값을 의미한다. 즉, 최빈값을 의미하는 것이다. 그런데 데이터 분포를 pdf로 표현해보면 다음과 같다.
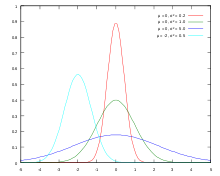
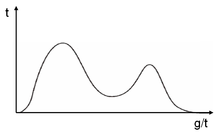
즉, 최빈값은 가장 높은 곳, peak인 지점을 의미하게 된다. 그래서 함수의 입장에서 mode란 peak를 의미하게 되는 것이다. 이때 위와 같이 하나의 peak만 가지는 함수들을 unimodal function이라 하고, 두 분포의 결합 등으로 2개의 peak를 가지게 되는 아래와 같은 경우는 bimodal distribution이라 한다.
가장 흔한 unimodal function으론 2차 단변량 함수가 있다.
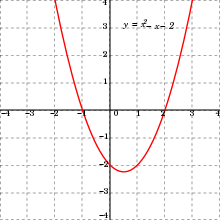
2차 단변량 함수는 당연하게도 위 혹은 아래로 볼록한 모습을 띄게 되므로 하나의 peak만 가지게 된다. 이러한 unimodal function에 대한 정의는 다음과 같다.
정의 : 함수 가 다음과 같은 유일한 점 을 가지고 있으면 unimodal function이다.
인 x에 대해 함수 가 단조 증가하고, 인 x에 대해 함수 가 단조 감소하면, 함수 는 을 critical point로 가진다.
이를 그래프로 표현하면 다음과 같다.
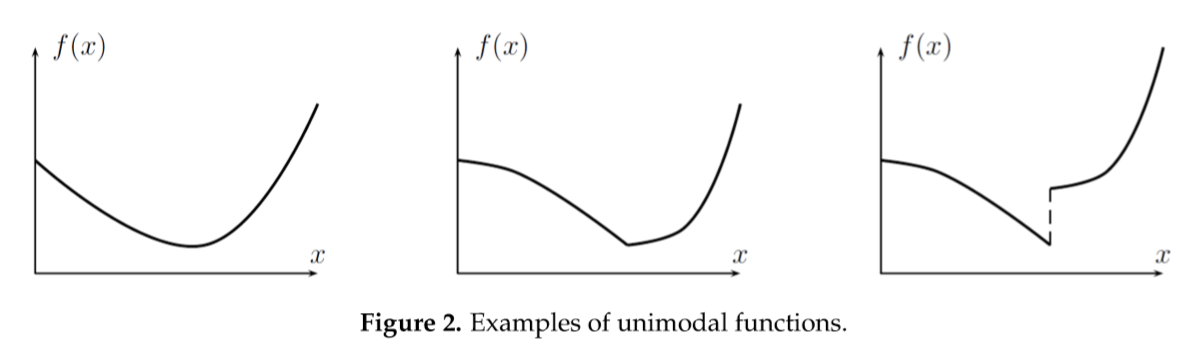
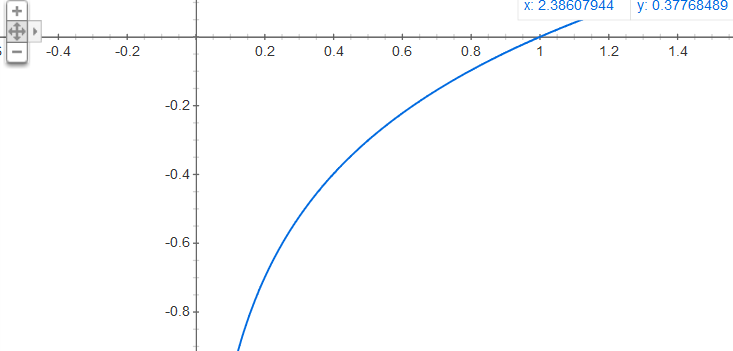
이러면 convex function과 무엇이 다른가 싶은데, 아래의 log(x) 함수는 concave function이지만 unimodality의 성질은 만족하므로, unimodal function이 된다.