개념

이전에 수강한 이상화 교수님의 수리 통계 수업에서도, 이번에 공부하는 최적화 책에서도 테일러 급수가 계속 나온다. 테일러 급수는 복잡한 함수를 간단한 함수로 근사할 수 있게 해주기 때문에 다양한 분야에서 그 쓰임이 다양한 것 같다. 정리하여 내 것으로 만들어보자. 테일

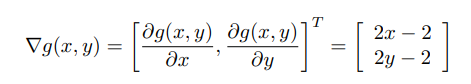
최적화 이론에서 그래디언트와 헤시안 행렬은 모두 함수에 대한 미분값을 표현하고자 한다는 점에서 비슷하다. 또한 두 값 모두 최적화 과정에서 사용된다는 점 역시 동일하다. 두가지에 대해 좀 더 자세히 살펴보도록 하자. 그래디언트는 함수를 편미분한 값을 원소로 하는 벡터를

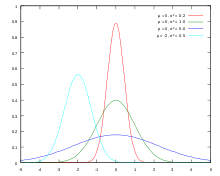
우선 mode가 무엇인지 이야기해보자. 모드는 통계학에서 자주 쓰이는 용어로 한 데이터 집합에서 가장 자주 등장하는 값을 의미한다. 즉, 최빈값을 의미하는 것이다. 그런데 데이터 분포를 pdf로 표현해보면 다음과 같다. 즉, 최빈값은 가장 높은 곳, peak인 지점을

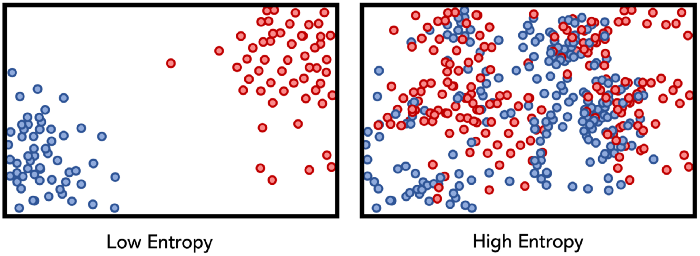
딥러닝은 범함수라는 이야기를 많이한다. SGD 등의 최적화를 통해서 우리가 원하지만 특정할 수 없는 어떠한 함수든 몇가지 조건만 만족하면 추정할 수 있다는 뜻이다. 이에 대해 여러가지 논문도 나온 것으로 알고, 이를 기반으로 지금까지 딥러닝이 그나마 수학적 배경을 갖추