KL Divergence & JS Divergence & Mutual Information

김재희·2021년 11월 1일

개념

목록 보기

4/4

Universal Approximation Theorem은 딥러닝이 충분히 깊다면 어떠한 연속함수든 근사할 수 있다는 이야기를 많이한다. SGD 등의 최적화를 통해서 우리가 원하지만 특정할 수 없는 어떠한 함수든 몇가지 조건만 만족하면 추정할 수 있다는 뜻이다. 이에 대해 여러가지 논문도 나온 것으로 알고, 이를 기반으로 지금까지 딥러닝이 그나마 수학적 배경을 갖추고 있는 것으로 안다.

생성모델들을 공부하면서 KL Divergence와 JS Divergence를 좀 생각해볼 기회가 있었는데, 한번 정리해보도록 하자. 많은 생성모델들이 실제 데이터가 특정한 분포를 따른다고 가정한다. 그 분포를 사전에 정의하면 VAE류의 모델이 될 것이고, 그저 추정하게 되면 GAN류의 모델이 된다. 학습을 통해 실제 데이터로 mapping할 수 있는 특정 분포를 알게 되었다고 해보자. 즉, 우리가 그 분포에서 데이터를 조정하면, 원하는 대로 실제 데이터 역시 생성할 수 있는 상황이다.

1. MSE & Cross Entropy

하지만 실제 분포와 추정된 분포는 당연히 차이가 있을 수 있다. 즉, 오차가 존재한다. 딥러닝에서 흔히 사용되는 MSE나 Cross Entropy를 이용하면 이러한 오차를 계산할 수 있을까? 답은 할 수 없다. MSE나 Cross Entropy는 정답 분포를 가정하지 않는다. 자세히 이야기해보자.

MSE와 CE는 사실 가정한 분포가 달라서 다르게 보이는 수식이다. MSE는 가우시안 분포에서, CE는 베르누이 분포에서 MLE를 풀 경우 자연스레 나오는 수식들이다. 이 두 수식 모두 그저 고정된 관측치에서 우도를 최대화하는 파라미터를 찾는 과정(MLE)에 불과하다. 즉, 원하는 분포가 고정되어 있지 않다. 실제로는 CE를 정답 분포의 정보량이 0인 상황에서 두 분포의 차이에 대한 식이라고 이야기할 수 있는데, one hot encoding을 분포라고 보기엔 애매하다고 생각한다.

2. Entropy

어떠한 분포의 정보량은 엔트로피로 나타낸다. 분포 p에 대한 엔트로피의 식은 다음과 같다.

\begin{aligned} H(p) &= -\mathop{\mathbb{E}}_{x\sim p}[\log p]\\ &=- \sum p(x) \log p(x) \end{aligned}

풀어서 이야기하면 엔트로피는 분포 $p$ 의 음의 로그 우도의 기대값이다. 즉, 분포의 각 지점에서의 음의 로그 우도 값의 기대값을 산출한 것에 불과하다. 여기서 음의 로그 우도는 MLE에서 최소화문제로 변환하고, 볼록함수로 만들기 위한 과정이므로 우도의 기대값이라 생각해도 무관할 것이다. 여기서 우도는 그렇다면 특정 지점에서의 정보량이라고 볼 수 있다.
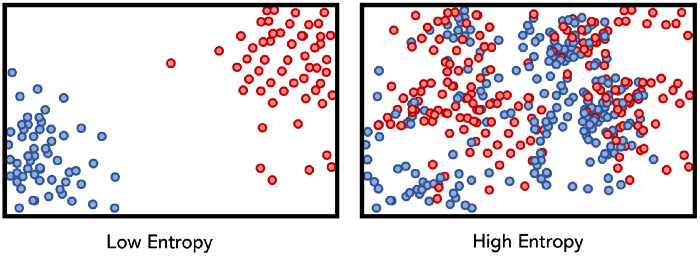
정보량이 많다는 것은 해당 분포의 불확실성이 높다는 뜻이다. 머신러닝의 관점에서 불확실성이 높은 것은 아직 추출해낼 정보가 많고, 더 많은 처리가 요구된다고 할 수 있다. 트리 기반 모델들이 정보량이 많은 변수를 기준으로 분기하는 것을 생각해보자. 아래 그림에서도 엔트로피가 낮으면 이미 어느정도 분류가 되어 초평면이 형성되어 있지만, 엔트로피가 높으면 아직 더 분류를 해야한다(분류라기 보단 mapping이라고 표현하는 것이 더 적절할 것 같다.).

3. Cross Entropy

CE는 우리가 알고있는 분포 $p$ 와 추정한 분포 $q$ 사이의 차이를 정보량을 통해 나타낸다.

\begin{aligned} H(p, q) &= -\mathop{\mathbb{E}}_{x\sim p}[\log q(x)]\\ &= -\sum_i p_i \log q_i\\ &= -\sum_i P(x \mid y) \log P(x \mid y, \theta) \end{aligned}

위의 수식을 풀어 이야기해보면 크로스 엔트로피는 우리가 현재의 파라미터 $\theta$ 에서 음의 우도의 기대값이라고 할 수 있다. 쉽게 이야기하면 우리가 근사하고 싶은 분포 $p$ 와 현재 파라미터 $\theta$ 하에서 추론한 $q$ 가 얼마나 비슷한지 그 차이를 계산한 것이다.

4. KL Divergence

KL Divergence 역시 CE처럼 두 분포 간의 차이를 나타낸다. 하지만 식이 조금 다르다. 위에서 $\log p$ 를 정보량이라고 한 것을 기억하면 두 분포의 차이는 각 지점에서 가진 정보량의 차이라고 볼 수 있을 것이다. 즉, 각 지점에서 두 분포가 동일한 정보량을 지니면 같은 분포라고 볼 수 있다. 이를 식으로 옮겨보면 다음과 같다. (여기서는 우리가 근사하고자 하는 분포가 $p$ , 추정한 분포가 $q$ 이다.)

한 지점에서의 두 분포의 정보량의 차이는 다음과 같다.

\log p(x) - \log q(x)

이를 분포 전체에 걸쳐 표현하면 다음과 같다.

\begin{aligned} D_{KL}(p \mid \mid q) &= \mathop{\mathbb{E}}_{x\sim p}[\log p(x) - \log q(x)]\\ &= \sum_i p_i(\log p_i - \log q_i)\\ &= \sum_i p_i\log {p_i \over q_i} \end{aligned}

즉, 위의 KL Divergence 식은 우리가 추정한 $p$ 에 대한 두 분포의 차이의 기대값이다.

여기서 KL Divergence 식을 조금 더 풀어서 보면 다음과 같은 점을 발견할 수 있다.

\begin{aligned} D_{KL}(p \mid \mid q) &=\sum_i p_i(\log p_i - \log q_i)\\ &= \sum H(p) + H(p, q) \end{aligned}

짜잔! KL Divergence 식을 풀어봤더니 엔트로피에서 크로스 엔트로피를 더한 식이 나왔다. 만약 $p$ 가 one hot encoding과 같은 categorical dist.라면 당연히 엔트로피가 0이 되므로 자연스레 우리가 알고있는 크로스 엔트로피 식이 나오게 된다. 일반적으로 분류 문제는 one hot encoding을 사용하므로 사실상 KL Divergence와 CE가 같은 식이 되는 것이다.

5. JS Divergence

위의 KL Divergence 식을 보면 $D_{KL}(p \mid \mid q) \neq D_{KL}(q \mid \mid p)$ 으로 symmetric하지 않은 것을 알 수 있다. 이는, KL Divergence가 실제 분포인 $p$ 를 기준으로 계산하기 때문이다. 물론 실제 분포 $p$ 에 $q$ 를 근사하기 위해 KL Divergence를 사용하면 문제가 없겠지만, 그냥 두 분포 간의 차이를 알기 위해서는 symmetric하지 못한 것은 문제가 된다. 결국 정답 분포는 없고, 두 분포 간의 거리만 알고 싶기 때문이다. 이를 해결하기 위해 KL Divergence 값을 수정한 것이 JS Divergence이다.

\begin{aligned} JSD(p, q) = {1\over 2}D_{KL}(p \mid\mid {p + q \over 2}) + {1\over 2}D_{KL}(q \mid\mid {p + q \over 2}) \end{aligned}

단순히 KL Divergence 식을 수정하여 symmetric하게 만든 것에 불과하다. 여기서 $p = q$ 일 경우 $JSD(p, q) = 0$ 으로 거리이기 위한 또다른 조건을 만족하고 있다.

6. Mutual Information

참고

https://theeluwin.postype.com/post/6080524 (이분 글이 크로스엔트로프나 젠센 부등식에 대해 아주 좋은 설명이라 생각한다.)
https://ratsgo.github.io/deep%20learning/2017/09/24/loss/
https://simpling.tistory.com/15
https://hyeongminlee.github.io/post/prob002_kld_jsd/
https://hyunlee103.tistory.com/102

김재희

이전 포스트