지금까지 다변량 목적함수를 최적화하는 방법에 대해 알아보았다. 이때 1계 조건에 의해 critical point를 찾고, 2계 조건을 통해 local minima와 global minimum을 분별하는 방법에 대해서 자세히 알아보았다.
그런데 local minima의 존재는 그래디언트 디센트라는 방법론에서 그렇게 좋지 못한 존재이다. local minima에 빠졌는지 확인할 수 있는 확실한 방법도 없고 (미분하여 확인하는 것이 힘들기 때문에 그래디언트 디센트를 사용할 것이다.), local minima에서 빠져나오는 것 역시 이로인해 쉽지 않다.

즉, 그래디언트 디센트 알고리즘에 있어 local minima의 존재는 불확실성을 키운다. 

그렇다면 그래디언트 디센트 알고리즘을 적용할 목적함수가 local minima가 없다면 훨씬 효과적으로 작동할 수 있을 것이다. 이와 같이 local minima가 없이 global minimum만 존재하는 함수를 convex function이라 한다. 우선 convex set에 대한 정의를 살펴보도록 하자.

1. Convex Set

convex set에 대한 정의는 다음과 같다.

집합 $C \subseteq R^n$에 속하는 두 점 $\bar{w_1}, \bar{w_2} \in C$에 대하여 선형결합 $\lambda\bar{w_1} + (1 - \lambda)\bar{w_2} \in C \; (\lambda \in (0, 1))$이라면 $C$는 convex set이다.

convex set에 대한 직관적 그림은 다음과 같다.

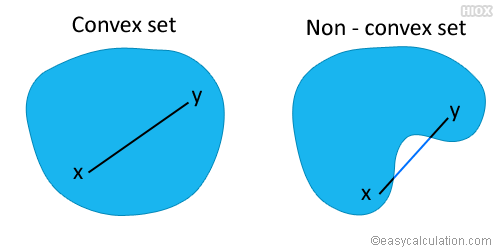
즉, 집합의 형태가 오목하게 들어간 부분이나 내부의 구멍이 없어 볼록한 집합을 이야기한다. 이를 위의 정의에 대입하여 생각해보면, 두 점에 대한 양의 계수이며 두 계수의 합이 1인 선형결합이 모두 그 집합에 속하는 경우를 의미한다. 쉽게 이야기하면, 집합 내부의 두 점에 대해 선을 그었을때, 그 선의 어느 한 점도 집합 외부로 나가지 않는 집합을 이야기한다.
이때 두가지 종류로 convex set을 또 나눌 수 있는데, 다음과 같다.

• Closed convex set : 집합의 경계면 또한 집합에 속하는 convex set을 의미한다.
• Open convex set : 집합의 경계면은 집합에 속하지 않는 convex set을 의미한다.

2. Convex Function

convex function에 대해 설명하기에 앞서 선형 함수의 성질을 잠시 짚고 넘어가자.

$f : R^m \to R^n$은 $f(x + y) = f(x + y)$이고 $f(ax) = af(x)$일때, 선형함수이다.

convex function은 $\lambda \in (0, 1)$에서 다음과 같이 정의할 수 있다(식 1).

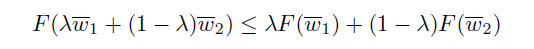
위의 수식을 만족하는 가장 단순한 예시는 아마 선형함수일 것이다. 위의 선형 함수의 성질 두가지를 이용하면 아래와 같이 선형 함수가 식 1에 부합함을 쉽게 보일 수 있다.

이때 선형함수에 대해서는 양 변의 식이 같은 값을 가지기 때문에 concave함수이기도 함을 알 수 있다. 즉, 선형함수는 convex 함수이면서 concave 함수이기도 한 독특한 성질을 가지고 있다.

또다른 예시로는 2차함수의 경우 2차항의 계수가 음이 아닌 경우 모두 convex function이다. 이는 위의 식에 2차 함수 $f(x) = ax^2 + bx +c$를 대입해 보아도 쉽게 알 수 있고, 2차함수의 모양을 생각보아도 쉽게 알 수 있다.

혹은 2차 함수를 위과 같이 표기할 때, P가 positive semidefinite이라면 f(x)는 아래로 볼록한 형태가 되기 때문에 convex function이 된다.

2-1. Properties of Convex Function

Convex function이 가지고 있는 성질은 다음과 같다.

1. convex function 간의 덧셈 혹은 합은 항상 convex function이다.
2. convex function에 대한 max function은 항상 convex function이다. 즉, 연속된 convex 함수들의 최대값을 이은 외각은 convex이다.
3. nonnegative한 convex function의 제곱은 항상 convex이다.
4. 만약 F(.)이 변수가 하나인 convex function이고, $G(\bar{w})$가 scalar output을 가지는 선형 함수라면, $F(G(\bar{w}))$는 convex 함수이다.
5. 만약 F(.)가 convex non-increasing function이고, $G(\bar{w})$가 scalar output을 가지는 concave function이라면,$F(G(\bar{w})))$는 convex 함수이다.

또한, Convex function이 가지지 않는 성질로는 다음과 같다.

1. 두 Convex 함수의 내적은 무조건 Convex하지 않다.

   $\begin{aligned} f(x) = x, g(x) = x^2\\ h(x) = f(x) \cdot g(x) = x^3 \end{aligned}$

   일때, h(x)는 convex 함수가 아니다.

2. 두 convex 함수의 합성 함수는 convex하지 않을 수 있다. 오히려 정의할 수 없거나, concave 함수일 수 있다.

   $\begin{aligned} f(x) = -x ,g(x) = x^2\\ h(x) = f(g(x)) = -x^2 \end{aligned}$

   이것은 딥러닝 분야에서 꽤 큰 의미를 가지고 있다. 딥러닝에서 각 레이어의 노드를 선형 결합으로 구성하여 convex function으로 만들 수 있지만, 각 레이어가 쌓이면서 합성함수의 꼴로 만들면서 convex function이 아닐 수 있다는 점을 기억하자.

아주 중요한 convex function의 성질이 하나 남아있다. 잘 생각해보면 당연히 그런 성질이다.

convex function의 모든 local minima는 global minimum이다.

convex function의 정의를 만족하면서 local minima는 global minimum과 동일하며, local minima에 빠져서 헤어나오지 못하는 문제가 convex function에서는 존재하지 않는다는 것을 의미한다. 즉, local/global minimum에 도달하기만 하면 global minimum에 도달했다는 의미가 된다.

2-2. Definition of Convex Function

위에서 언급한 convex function에 대한 정의 외에도 다른 방식의 정의가 있다. 한번 살펴보도록 하자.

• First-Derivative Characterization of Convexity
  convex 함수의 1차 미분은 다음과 같은 특징이 있다.

  $F(\bar{w}) \geq F(\bar{x_0}) + [\nabla F(\bar{x_0})] \cdot (\bar{w} - \bar{w_0}) \tag{2}$

  위 식에서 주목할 점은 만약 함수 $F(\bar{w})$의 그래디언트가 $\bar{w} = \bar{x_0}$에서 0이라면 어떠한 $\bar{w}$에 대해서도 $F(\bar{x} \geq F(\bar{w_0})$가 성립한다. 즉, $w_0$가 global minimum이며, 어느 critical point도 1차 미분 조건을 만족한다면 global minimum임을 의미한다.
  위의 식은 convex function임을 알아내는데 좋은 식이지만 미분가능한 함수에 대해서만 적용가능하다는 한계점이 있다.

• Second-Derivative Characterization of Convexity
  convex 함수의 2차 미분은 다음과 같은 특징을 가지게 된다. 즉, 다음과 같은 특징은 함수 F(.)가 convex function이기 위한 필요조건이다.

  함수 $F(\bar{x})$가 모든 파라미터 $\bar{w}$에 대해 positive semi-definite을 가지는 헤세 행렬을 가진다.

이를 정리하면 convex function을 총 3가지 방법으로 정리할 수 있다는 것을 알 수 있다. 다음과 같이 정리할 수 있겠다.

2차 미분이 가능한 함수 F가 $R^n$에 대해 정의되어 있을 때, 다음 조건은 모두 동일하게 F가 convex function임을 가르킨다.

• Direct : The convexity condition $F(\lambda \bar{w_1} + (1 - \lambda)\bar{w_2} \leq \lambda F(\bar{w_1}) + (1 - \lambda)F(\bar{w_2})$ is satisfied for all $\bar{w_1}, \bar{w_2}$ and $\lambda \in (0, 1)$
• First-derivative : The first-derivative condition $F(\bar{w}) \geq F(\bar{w_0}) + [\nabla F(\bar{x_0})] \cdot (\bar{w} - \bar{w_0})$ is satisfied for all $\bar{w} \; and \; \bar{w_0}$
• Second-derivative : The Hessian of $F(\bar{w})$ is positive semidefinite for all $\bar{w}$

지금까지 배운 convex function에 대한 정의와 성질들은 모두 그 쓰임새가 있다. 위 세가지 정의 중 어느 것을 사용하더라도, 문제는 없지만 Direct 정의가 가장 많이 쓰인다. 다른 두 정의는 미분가능성이 보장되어야 하기 때문이다. 예를 들어 $F(x) = \lvert x\rvert$는 convex function이지만 $x = 0$에서 미분 가능하지 않기 때문에, 아래 두 정의로는 convex function임을 확인할 방법이 없다.
또한, convex 함수의 성질을 이용하면, 전체 함수의 convexity를 확인할 필요없이 함수의 일부분만 확인해도 충분한 경우가 있다. 예를 들어 함수 $F(G(\bar{w}))$에서, $F(.)$는 단변량 함수이고, $G(\bar{w}) = \bar{w} \cdot \bar{X}^T$인 선형 함수라면, $F(.)$가 convex 함수인지만 확인한다면 충분할 것이다.

3.Strict Convexity

convexity condition을 조금 변경하면 strict convexity에 대한 정의가 된다.

strict convexity란 위의 식에서 보이듯이 unique global minimum을 가진다. 즉, 기존의 convexity가 밥그릇처럼 일종의 평평한 바닥(연속적인 global minimum)을 가질 수 있지만, strict convexity는 등호가 제거되었기 때문에 global minimum과 동일한 값을 가지는 neighbor이 존재하지 않는다. 또한, 등호가 제거되었기 때문에, 당연하게도 saddle point도 가질 수 없다.
strict convexity에 대한 first-order condition은 아래와 같이 쉽게 제시할 수 있지만, second-order condition은 일반화되지 않는다고 한다. 헤세 함수가 positive definite을 가지고 있으면, 항상 strict convexity를 가지지만, 그 역은 성립하지 않기 때문이다.

최적화에서 strict convexity가 유용한 이유는 stirct convexity는 결국 하나의 critical point를 가지기 때문이다. 또한, convex function과 strictly convex function의 합은 항상 strictly convex function이 된다.

머신러닝 분야의 많은 목적함수가 convex한 형태(l2 norm 등)를 가지고 있는 것을 생각해보면, strict convex regualarizer를 추가하는 간단한 방법으로 목적함수를 strictly convex function으로 만들 수 있다.

후에 나올 이야기지만 조금만 더 설명해보면, quadratic convex function의 경우 특별한 convex function이라고 할 수 있다 왜냐하면 본래 헤세 행렬은 파라미터 w에 대한 함수꼴이기 때문에, 특정 point에 대한 값을 나타내지만, quadratic convex function의 경우에는 상수로 이루어져 있기 때문이다(2차함수를 2차미분하면 상수가 되는 것은 자명하다.). 이를 이용해 quadratic convex function을 아래와 같이 표기할 수 있게 된다.

이때 convex function은 local minimum이 없기 때문에 gradient descent를 이용해 항상 global minimum에 근접할 수 있게된다. 만약 딥러닝 모델과 같이 목적함수가 복잡해지더라도, 목적함수가 convex하지 않더라도 근접한 경우가 많기 때문에, gradient descent가 잘 동작한다고 한다.
또한 함수 $F(\bar{w})$가 convex하다면 $F(\bar{w}) \leq b$와 같은 지역도 convex set임을 이용해 복잡한 최적화 문제를 간단히 해결할 수 있다고 한다.

---

참고

모두를 위한 컨벡스 최적화
Charu C. Aggarwal - Linear Algebra and Optimization for Machine Learning