1. Bivariate Optimization

1-1. Gradient

이전에 단변량 최적화에 대해 생각해보았다면 이를 일반화하여 다변량 최적화를 다뤄보고자 한다. 이때 그 중간다리로서 이변량 최적화에 대해 잠시 다루고 넘어가자.

다음과 같은 두 함수가 있다고 해보자

이때 두 함수 모두 두 변수 간의 상호 항이 없이 단변량 함수 두개의 덧셈꼴로 표현된 함수로 addictively separable한 상황이라고 부른다고 한다. 뒤에서 배우겠지만 모든 2차 함수는 addictively separable form으로 나타낼 수 있다고 한다.

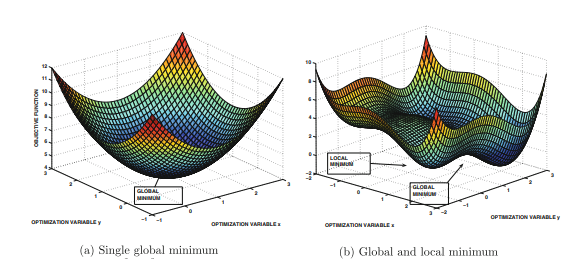
위의 그림이 두 함수를 시각화 한 것이다. 여기서 두 함수를 모두 하나의 변수를 축으로 단면적을 잘라보면 어떤 변수를 선택하든 비슷한 모습을 가진다는 것을 알 수 있을 것이다. 이때 a 그림은 global optimal 하나만 가지고 있지만 b 그림은 여러개의 local optimal과 하나의 global optimal을 가지고 있는 것을 알 수 있다. 두 함수에 대해 그래디언트 디센트를 시행하기 위해서는 편미분(partial derivative)를 이용해야 한다. 편미분이란 다변량 함수에 대해 하나의 변수를 기준으로 미분하는 것으로 다른 변수들은 상수로 간주하게 된다. 즉, 위에서 언급한 단면적으로 자른 경우의 모습에서 미분하는 것과 같다. 사실 gradient라는 용어 자체가 편미분을 이용해 구한 벡터라고 한다. 즉, 함수에서 현재 지점을 원점으로 삼고 optimal point로 방향이 향해 있으며(항상 이렇지는 않다), 현재의 기울기에 비례한 크기를 가지는 벡터가 되는 것이다.

g(x,y)를 편미분하여 그래디언트를 구하면 다음과 같다.

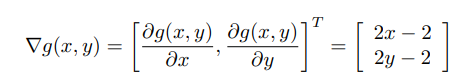
이때 $\nabla$는 해당 함수의 그래디언트를 의미한다. 만약 $\nabla_x f(x, y, z)$라 표기되어 있다면, x, y, z를 변수로 가지는 다변량 함수 f에 대해 x로 편미분한 그래디언트를 의미한다. 위의 식으로 다시 돌아오면 그래디언트란 즉, 각 변수로 편미분한 값으로 구성된 벡터라고 할 수 있다. 또한, 최적화 문제를 해결한다는 것은 그래디언트가 0이 되는 지점을 찾는 문제가 된다. global optima는 모든 변수에 대한 기울기가 0일 것이기 때문이다. 즉, 그래디언트가 0이 되는 지점을 찾는 것은 first order condition을 맞추는 일이고, 후에 배울 방법을 통해 벡터 단위에서 second order condition을 맞추면 optimal point를 찾을 수 있게 된다. 하지만 아쉽게도 상기했듯이 대부분의 경우에서 closed form의 방정식의 형태로 풀이 할 수 없다. 이때 그래디언트 디센트가 등장하게 된다.

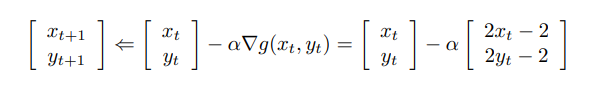
이변량 함수에 대한 gradient descent update는 위의 수식과 같이 진행되는데, $\nabla g(x_t, y_t)$가 x와 y에 대한 단변량 함수꼴이라는 점을 생각해보면 결국 스칼라 단위로 생각하면 앞에서 배운 단변량 함수에서의 그래디언트 디센트를 벡터로 확장한 것에 지나지 않는다.

지금까지는 Addictively Separable한 함수만 다뤄봤다. 그렇다면 Addictively Separable하지 않은 함수의 경우에는 어떻게 될까.

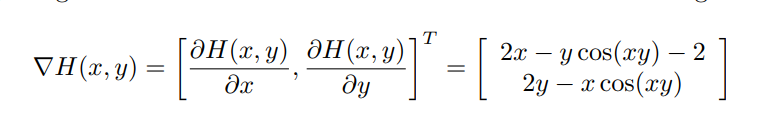
물론 각 변수에 대한 편미분에서 다른 변수가 등장하기는 하지만, 이전과 크게 달라지지 않은 모습이다.

1-2. Critical Point

이외에도 단변량 최적화와 마찬가지로, 이변량 최적화시에도 local optima의 존재는 consistent problem을 발생시킨다. 위에서 살펴본 G(x, y)함수를 살펴보자.

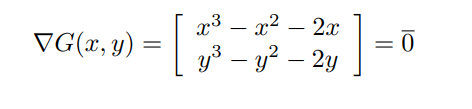
여기서 $(x, y) \in \{-1, 0, 2\} \times \{-1, 0, 2\}$인 총 9가지의 경우에 모두 1계조건(foc)를 만족시키는 critical point가 된다. 이 중 하나의 global minimum, 3개의 local minima, 하나의 local maximum을 가지게 되고, 이외의 4개의 점은 모두 안장점이된다. 하지만 어떤 점이 안장점, maximum, minimum인지 판별하기 위해서는 2계조건을 확인해야 한다. 2계 조건은 다변량 최적화에서 살펴볼 것이다. 중요한 것은 단변량을 너머 다변량이 되면서 확인해야할 critical point가 기하급수적으로 늘어난다는 것이다. 왜냐하면 각 변수마다 critical point를 구성하는 값이 존재하고, 모든 값의 조합이 모두 critical point가 되기 때문이다.

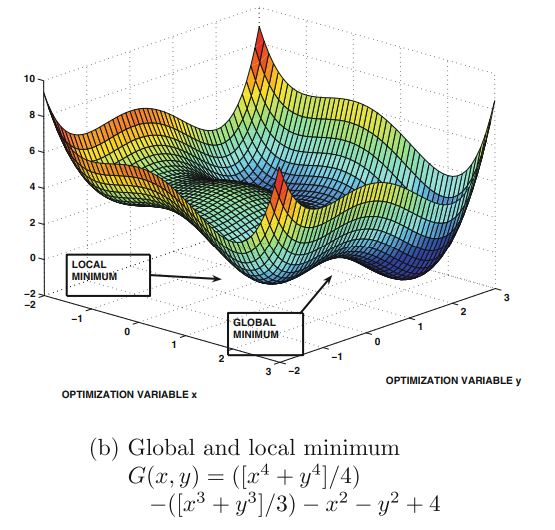
위의 함수에서 4개의 minima가 볼록한 형태로 존재하게 되는데, 초기값에 따라 그래디언트가 흘러서 도착하게 될 minimum이 달라지게 된다. 이때, 적절한 초기값을 가지지 못하면 local minima에 빠지게 될 우려가 있다. 이를 해소하기 위해서는 learning rate을 높여서 local minima에서 overshoot할 수 있도록 해야한다. 즉, starting point와 learning rate이 학습에 중요한 세부 요소임을 알 수 있다.

2. Multivariate Optimization

기계 학습은 대부분의 경우에 변수가 매우 많은 상황에서 이루어지게 된다. 즉, 최적화 문제에서 변수란 예측에 사용하는 함수를 구성하는 파라미터를 의미한다. 이외에도 학습 시 사용하게 되는 실제 관측치가 있는데, 이 역시 변수라고 표현하기는 하나, 최적화 문제에서는 상수로 취급된다.
관측치가 다음과 같은 튜플의 형태로 존재한다고 해보자.

1차 회귀식으로 간주하고 손실함수를 구성하면 다음과 같을 것이다.

또한 손실값은 모든 튜플에서 발생한 손실의 총합으로 표현되게 된다. 이때의 목적함수를 우리는 손실함수라고 부른다. 이때, 파라미터 $w_i$가 다수 존재하는 것을 확인할 수 있고, 이를 벡터로 표현하여 $\bar{w} = [w_1 ... w_d]^T$로 표기하고, $ $J(\bar{w})$ 같이 손실함수를 표현할 수 있다. 이때의 d는 파라미터의 갯수를 의미한다.

이변량 최적화에서의 편미분이 다변량 최적화와 다른 점은 이변량 최적화를 일반화 하여 다변량 최적화를 구성하게 된다는 점이다. 즉, 아래와 같이 편미분을 표현하게 된다.

이는 결국 d개의 연립방정식을 의미하게 되는데. 이를 이용해 1계 조건을 만족하는 critical point 중에 2계 조건을 만족하는 maximum, minimum 을 찾게 된다. 이때, 단변량 최적화처럼 직접 방정식을 풀지 않고 행렬을 이용해 계산하게 된다. 이때 이용하는 행렬이 Hessian Matrix이다. 헤세 행렬(H)은 결국 2차 미분 $f''(w)$를 일반화시킨 것이라고 볼 수 있다. 만약 손실함수 $J(\bar{w})$가 2차 함수의 꼴을 띄고 있다면, 당연히 헤세 행렬은 $\bar{w}$에 독립일 수밖에 없다. 단변량 최적화에서 함수가 2차 함수라면, $f''(w)$가 상수를 이루고 있는 것의 일반화인 것이다.
이때 그래디언트와 동일하게 헤세 행렬도 본래는 파라미터를 입력값으로 가지는 함수의 꼴이다. 하지만 표기 상의 편의를 위해 H라고만 표기하자.
헤세 행렬을 이용해 2계 조건을 확인하기 위해선 헤세 행렬이 양 혹은 음의 정부호 행렬인지 확인해야 한다. 이는 손실함수에 대한 테일러 급수를 통해 확인한다. 현재 지점 $\bar{w_0}$에서 임의의 방향 $\bar{v}$로의 손실함수를 테일러 급수를 통해 2차 항까지 전개해보면 다음과 같다(이때 $\epsilon$은 양의 아주 작은 수로 $\bar{x_0}$ 주변의 국소적 지점을 의미하기 위해 사용된다.).

여기서 우리는 1계 조건을 만족하는 $\bar{w_0}$를 찾은 상태라면 두번째 항의 $\nabla J(\bar{w_0})$이 0이 되므로 다음과 같이 정리된다.

이때의 헤세 행렬은 당연히도 파라미터 벡터 $\bar{x_0}$에 대한 행렬이다. 만약 해당 지점 $\bar{x_0}$이 최소값을 가지는 지점이라면 주변의 어느 방향과 비교해도 가장 작은 손실함수를 가져야 한다. 즉, $J(\bar{w_o} + \epsilon\bar{v}) > J(\bar{w_0})$이어야 한다. 반대로 $\bar{x_0}$이 최대값을 가지는 지점이라면 주변의 어느 방향과 비교해도 가장 큰 손실함수를 가져야 한다. 즉, $J(\bar{w_o} + \epsilon\bar{v}) < J(\bar{w_0})$이 되어야 한다. 만약 $\bar{x_0}$이 안장점이라면 해당 지점 주위로는 $\bar{x_0}$보다 큰 손실함수를 가지는 지점도 있고, 작은 손실함수를 가지는 지점도 있어야 한다. 즉, $J(\bar{w_o} + \epsilon\bar{v})$와 $J(\bar{w_0})$은 비교가 불가능해야 한다.

이때 위에 내가 걸어논 링크에서 설명해놨듯이 헤세 행렬의 정부호 행렬 여부에 따라 다음과 같이 정리 할 수 있다.

1. 헤세 행렬이 양의 정부호 행렬일 경우 : $\bar{x_0}$는 local minimum이다.
2. 헤세 행렬이 음의 정부호 행렬일 경우 : $\bar{x_0}$는 local maximum이다.
3. 헤세 행렬이 부정부호 행렬일 경우 : $\bar{x_0}$는 안장점이다.
4. 헤세 행렬이 양 혹은 음의 준정부호 행렬일 경우 : 위의 세가지 경우 중 어느 것인지
   확인 할 수 없다.

헤세 행렬에 대해 조금 더 설명하자면, 헤세 행렬은 결국 손실함 수 $J(\bar{w})$를 두 번 편미분한 행렬이다. 즉, 헤세 행렬은 손실함수의 곡률에 대한 정보를 가지고 있는 것이다. 헤세 행렬은 결국 $\bar{w}$에서 손실함수가 가지는 곡률을 서로 직교하는 벡터(아이겐 벡터)로 표현하고 있는 것이다. 헤세 행렬의 아이겐 벡터가 향하는 방향에 아이겐 벨루만큼의 크기로 곡률을 가지고 있으니, 모든 곡률이 동일한 부호를 가진다면 minimum 혹은 maximum이 되는 것이고, 곡률의 부호가 다른 방향이 하나라도 있다면 saddle point가 되는 것이다.