최적화 이론

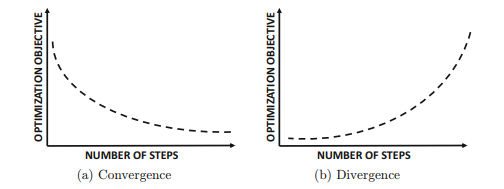
머신러닝의 가장 간단한 모델은 선형회귀 식일 것이다. 선형회귀식은 최소제곱법을 이용하여 식을 데이터에 적합시킨다. 선형회귀식은 다르게 보면 행렬로 볼 수도 있는데, 이때는 $Ax = y$와 같은 형태가 되고, 이때 consistent한 방정식이라면 오차가 0이 되는 x

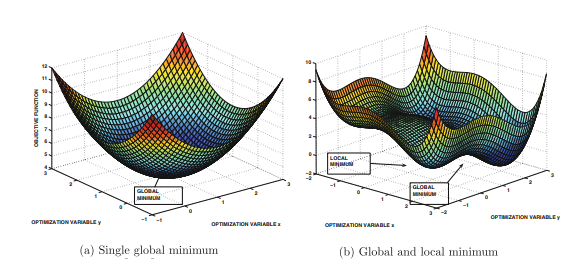
이전에 단변량 최적화에 대해 생각해보았다면 이를 일반화하여 다변량 최적화를 다뤄보고자 한다. 이때 그 중간다리로서 이변량 최적화에 대해 잠시 다루고 넘어가자. 다음과 같은 두 함수가 있다고 해보자$$g(x, y) = f(x) + f(y) = x^2 + y^2 - 2x

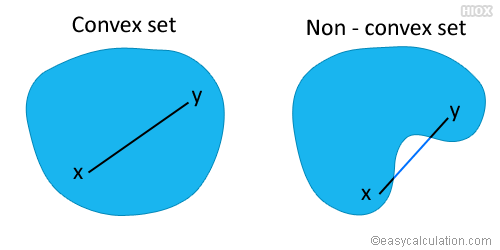
지금까지 다변량 목적함수를 최적화하는 방법에 대해 알아보았다. 이때 1계 조건에 의해 critical point를 찾고, 2계 조건을 통해 local minima와 global minimum을 분별하는 방법에 대해서 자세히 알아보았다. 그런데 local minima의

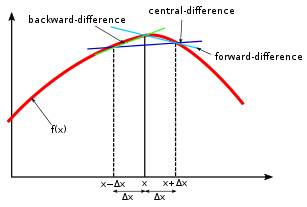
최근에서야 딥러닝 모듈이 워낙 잘 되어 있어 역전파에서 오류가 발생할 일은 자주 없다. 특히 개발자나 연구자가 이를 따로 신경쓸 필요가 없다. 역전파에서 오류가 났다면, 모듈이 잘못되었을 가능성보다 코딩에 문제가 있을 가능성이 높을 것이다. 하지만 과거에 인공신경망을

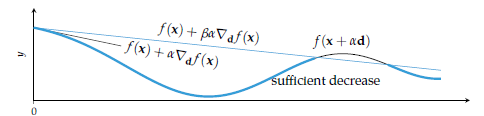
이 장에서는 국지적으로 근사한 모델을 통해 목적함수를 최소화하는 방향으로 반복적으로 조금씩 이동하는 알고리즘들을 살펴보게 될 것이다. 이는 Descent Direction Method라 하며 내가 알고 있는 대표적인 모델은 Gradient Descent인 것 같다. 자

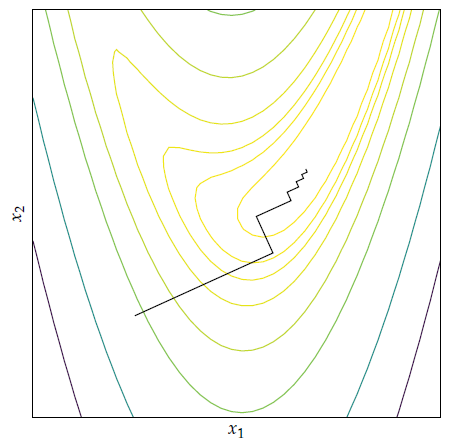
1계 도함수법은 현재 위치에서의 기울기를 이용해 최적해를 찾는다. 이때 반복적인 작업을 통해 최적해를 찾아나가게 된다. 이번에 다룰 내용은 기본적인 그래디언트 디센트부터 딥러닝 옵티마이저로 자주쓰이는 Adam 등, 매우 자주 접하게 되는 최적화기법들이다. 이전에도 다룬

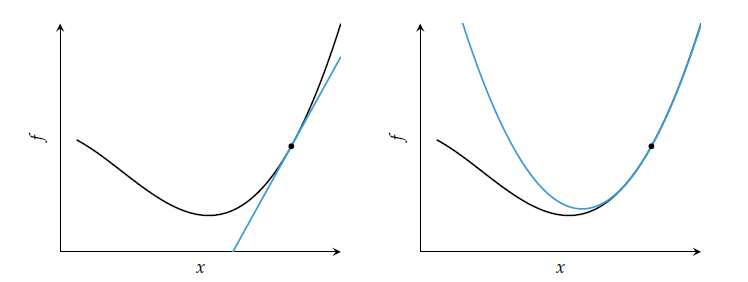
1계 도함수법은 그래디언트를 이용해 목적함수의 1차 근사를 하는 최적화 방법이다. 이에 비해 2계 도함수법은 헤시안 등을 사용해 2차 근사를 이용한다. 1계 도함수법에 비해 많은 정보를 활용하기 때문에, 더욱 정확한 근사를 기대할 수 있을 것이다. 그래디언트는 최적해로

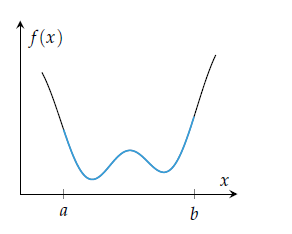
지금까지는 주어진 목적함수에 대해 최소화하는 다양한 방법들을 살펴보았다. 하지만 실제로는 단순히 목적함수만 주어지지 않는다. 선형회귀에서도 랏소나 릿지와 같이 가중치들에 대한 제약식이 주어진다. 이렇게 제약식이 주어졌을 때, 어떻게 문제를 해결할 수 있는지 알아보자.

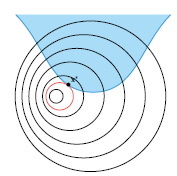
앞서 등식 제약조건에서 어떻게 라그랑주 승수를 이용해 라그랑지안을 정의하는지 살펴보았다. 그렇다면 부등식 제약조건에서는 어떻게 최적해를 구할 수 있을까?우선 다음과 같은 부등식 제약 조건이 있다고 생각해보자. $$minimize\_{\\textbf{x}} f(\\tex